Правильный четырехугольник в основании призмы
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия - призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
При решении задач на тему "правильная четырехугольная призма" подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.
То есть правильная четырехугольная призма содержит в своем основании квадрат.
Задача.
В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник - это квадрат.
Соответственно, сторона основания будет равна √144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )2 + 142 ) = 22 см
Ответ: 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
Параллелограмм в основании призмы
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
Задача
Основанием прямой призмы ABCD A1B1C1D1 является параллелограмм ABCD со сторонами 4 см и 4√3 см и углом, равным 30 градусов. Диагональ AC1 призмы образует с плоскостью основания угол в 60 градусов. Найдите площадь боковой поверхности призмы.
Решение.
Поскольку сумма соседних углов параллелограмма равна 180 градусам, то углы B и D. будут равны 180 - 30 = 150 градусов.
Диагональ параллелограмма AC, таким образом, образует треугольник ACD с углом C равным 150 градусов.
Применим теорему косинусов, при этом обозначив диагональ параллелограмма как d, а стороны параллелограмма как a и b. Учтем, что косинус 150 градусов равен cos( 150° ) = -√3 / 2. Получим:
d2 = a2 + b2 - 2abcos( 150° )
d2 = 16 + 48 - 2 * 4 * 4√3 * ( -√3 / 2 ) = 112
d = 4√7
AC = 4√7
Зная величину диагонали параллелограмма, найдем высоту параллелограмма. Треугольник, который образует диагональ AC1 ( AC1С ) с основанием призмы, согласно условию задачи (призма - прямая) является прямоугольным. Угол ∠C1AC по условию равен 60 градусов. Для прямоугольного треугольника тангенс угла ∠C1AC равен отношению противолежащего катета к прилежащему, то есть tg ( ∠C1AC ) = C1С / AC . Учтем, что тангенс 60 градусов равен tg 60° = √3.
Соответственно, C1С = AC tg ( ∠C1AC )
C1С = 4√7 * tg60°
C1С = 4√21
Зная высоту призмы, определим площадь ее боковой поверхности:
S = 2ha + 2hb
S = 2 * 4 √21 * 4 √3 + 2 * 4 √21 * 4 = 96√7 + 16√21 ≈ 327,31
Ответ: 96√7 + 16√21 ≈ 327,31
Ромб в основании призмы
Задача.
Основание прямой призмы - ромб с углом 120 градусов. БОльшая диагональ призмы равна 8см и составляет с боковым ребром угол 60 градусов. Найти сторону ромба и меньшую диагональ призмы.
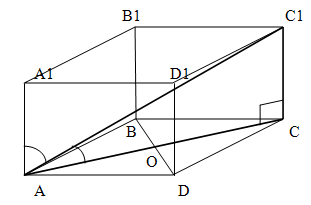
Решение.
Поскольку диагональ AC1 образует с ребром AA1 угол 60 градусов, призма является прямой, то угол C1AC равен 90 - 60 = 30 градусов.
Исходя из этого cos 30 = AC / AC1 = √3 / 2
AC / AC1 = √3 / 2
AC / 8 = √3 / 2
2AC = 8√3
AC = 4√3
Поскольку угол ADC равен 120 градусам, то угол BAD равен 60 градусам. (Сумма углов выпуклого четырехугольника равна 180(n-2) = 360 градусам, углы ромба попарно равны).
Исходя из того, что угол BAD равен 60 градусам, треугольники ABD и BDC- равносторонние. (Так как ABCD - ромб, то они равнобедренные, следовательно углы при основании равны, значит они равны ( 180 - 60 ) / 2 = 60 градусов. Треугольник, у которого все углы равны - равносторонний).
Диагонали параллелограмма в точке пересечения делятся пополам. Таким образом, AO = AC / 2 = 4√3 / 2 = 2√3
Поскольку треугольник ABD правильный, то AO является одновременно высотой и биссектрисой. Учтем, что высота правильного треугольника равна
h = а √3 / 2, тогда
а √3 / 2 = 2√3
а = 4
Зная, что BD = 4 см, DD1 = 4 см, по теореме Пифагора найдем меньшую диагональ:
BD12 = 4 + 4
Таким образом, сторона ромба равна 4 см, а, так как треугольники ABD и BDC- равносторонние, то и меньшая диагональ ромба равна 4 см.
Для того, чтобы найти длину ребра призмы, учтем, что диагональ AC1 = 8 см, а угол C1AC = 30 градусам. Тогда sin 30 = C1C / AC1 = 1/2
C1C / 8 = 1/2
C1C = 4 см
Зная что BD = 4 см (меньшая диагональ ромба), D1D = 4 см (ребро призмы), длину меньшей диагонали призмы найдем по теореме Пифагора:
BD12 = DD12 + BD2
BD12 = 42 + 42
BD12 = 32
BD1 = 4√2
Ответ: Сторона ромба - 4 см, меньшая диагональ призмы с ромбом в основании равна 4√2 см.
Параллепипед
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия - параллелепипед). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
При решении задач, учитывайте определение параллелепипеда:
Параллелепипед— призма, основанием которой служит параллелограмм.
Задача
Основанием параллелепипеда служит квадрат. Одна из вершин его верхнего основания одинаково удалена от всех вершин нижнего основания. Определите высоту параллелепипеда, если диагональ основания равна 8 см, а боковое ребро равно 5 см.
Решение.
Поскольку одна из вершин основания параллелепипеда (обозначим ее F) одинаково удалена от всех вершин нижнего основания параллелепипеда, то вместе с диагональю нижнего основания (обозначим ее AC) она образует равнобедренный треугольник AFC. AF = AC по условию. Одновременно, AF - это ребро параллелепипеда.
Таким образом, в равнобедренном треугольнике AFC стороны равны следующим величинам: AF=FC=5 см , AC = 8 см.
Высота равнобедренного треугольника AFC одновременно, будет являться высотой параллелепипеда. Пусть она опущена в точке K.
Кроме того, высота равнобедренного треугольника делит его основание пополам. Откуда, по теореме Пифагора высота будет равна:
FK2 + (AC/2)2 = FC2
FK2 + 16 = 25
FK2 = 9
FK = 3 см
Ответ: высота параллелепипеда равна 3 см.
Задача
Найти площадь основания ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 если DB1 = 6 см, DB = 5 см, BC1 = 4 см.
Решение.
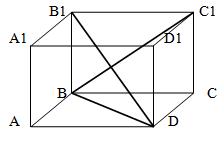
Для нахождения длин сторон ( поскольку параллелепипед в условии задачи прямоугольный, а значит, все ребра пересекаются под прямым углом ) используем теорему Пифагора.
Найдем BB1 в прямоугольном треугольнике DBB1
BB1 = √( B1D2 - BD2 )
BB1 = √(36 - 25) = 3
Соответственно
СС1 = BB1 = 3 см
Для прямоугольного треугольника BC1C
BC = √( BC12 - C1C2 )
BC = √( 16 - 9 ) = √7
В треугольнике BCD найдем CD
CD = √( BD2 - BC2 )
CD = √( 25 - 7 ) = √18 = 3√2
Откуда площадь основания параллелепипеда равна:
S = BC * CD = √7 * 3√2 = 3√14
Ответ: площадь основания прямоугольного параллелепипеда равна 3√14
Параллелепипед (часть 2)
Примечание. Это часть урока с задачами по геометрии (раздел теорема стереометрия - параллелепипед). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√"
Задача.
Основание прямоугольного параллелепипеда - ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны P и Q
Решение.
Площадь первого сечения выразим как
P = hd1 , где
h - высота параллелепипеда
d1 - длина диагонали
Площадь второго сечения выразим как
Q= hd2 , где
h - высота параллелепипеда
d2 - длина диагонали
Соответственно,
d1 = P / h
d2 = Q / h
Площадь боковой поверхности равна
S = 4ah, где
a - длина стороны ромба
h - высота параллелепипеда
По теореме Пифагора
a = sqrt( ( d1 / 2 )2 + ( d2 / 2 )2 )
a = sqrt( d12 / 4 + d22 / 4 )
a = sqrt( d12 + d22 ) / 2
Тогда
S = 4ah
S = 4h sqrt( d12 + d22 ) / 2
S = 2h sqrt( d12 + d22 )
поскольку
d1 = P / h
d2 = Q / h
то
S = 2h sqrt( ( P / h )2 + ( Q / h )2 )
S = 2h sqrt( P 2 + Q2 ) / h
S = 2 sqrt( P 2 + Q2 )
Ответ: S = 2 √( P 2 + Q2 )
Пирамида. Решение задач
