Работа. энергия. законы сохранения

Краткая теория

Система тел (частиц) называется замкнутой, если на нее не действуют внешние силы. Силы, обусловленные воздействием тел, не принадлежащих системе, называются внешними. В соответствии с основным уравнением динамики поступательного движения 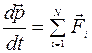( 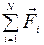- геометрическая сумма внешних сил, действующих на систему) импульс системы может изменяться под действием только внешних сил. Внутренние силы не могут изменить импульс системы.

Закон сохранения импульса: импульс замкнутой системы тел (частиц) остается постоянным, т. е. не меняется со временем

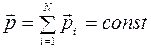. (5.1)

При этом импульсы отдельных частиц или частей замкнутой системы могут изменяться со временем. Импульс может сохраняться и у незамкнутой системы при условии, что результирующая всех внешних сил равна нулю.

Закон сохранения проекций импульса на оси декартовой системы координат:

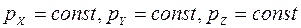. (5.2)

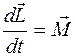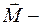Согласно основному уравнению динамики вращательного движения (где суммарный момент внешних сил, действующих на систему) момент импульса системы может изменяться под действием только суммарного момента всех внешних сил.

Закон сохранения момента импульса:момент импульса замкнутой системы частиц остается постоянным, т. е. не меняется со временем 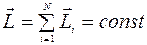. (5.3)

Элементарная работа силы 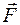на перемещении :

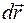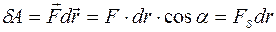, (5.4)

где 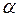- угол между векторам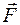и и 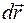, F_S – проекция вектора 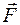на направление вектора 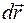. Суммируя выражение (5.4) по всем элементарным участкам пути от точки 1 до точки 2, можно найти работу силы на данном пути:

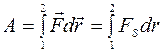. (5.5)

Работа внешних сил при вращении твердого тела вокруг неподвижной оси определяется действием момента M_Z этих сил относительно данной оси Z:

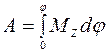, (5.6)

где 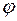- конечный угол, на который поворачивается твердое тело. Для характеристики скорости, с которой совершается работа, вводят величину, называемую мощностью:

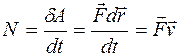. (5.7)

Таким образом, мощность, развиваемая силой 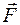, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы. Как и работа, мощность – величина скалярная.

Кинетической энергией Т теланазывается энергия механического движения этого тела. Кинетическая энергия поступательного движения тела:

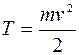
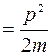. (5.8)

где m-масса тела, v – скорость центра инерции тела.

Кинетическая энергия вращательного движения тела вокруг оси, проходящей через его центр инерции:

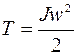, (5.9)

где J и w– момент инерции и угловая скорость тела.

Кинетическая энергия тела, катящегося по плоскости без скольжения:

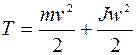. (5.10)

Консервативныминазываются силы: 1) работа которых не зависит от пути по которому движется тело (частица), а определяется только начальным и конечным положением тела; 2) работа которых на любой замкнутой траектории равна нулю. Пример консервативной силы – сила тяжести, сила упругости, неконсервативной – сила трения. Работа консервативных сил на пути 1-2 равна убыли потенциальной энергии тела (частицы) в данном поле:

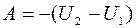. (5.11)

Потенциальной энергиейU системы тел (частиц) называется энергия, обусловленная взаимным расположением тел, действующих друг на друга.

Работа результирующей всех сил, действующих на тело (частицу), идет на приращение кинетической энергии тела (частицы):

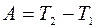. (5.12)

Полная механическая энергия тела (частицы) в поле:

E=T+U (5.13)

Закон сохранения полной механической энергии:полная механическая энергия тела (системы тел), на которое действуют только консервативные силы, остается постоянной.

E=const. (5.14)

Приращение полной механической энергии тела (системы тел, частиц) на некотором пути равно работе неконсервативных (сторонних) сил, действующих на тело на том же пути:

A_ст=E₂-E₁ (5.15)

Вопросы для самоподготовки

1. Дайте определение замкнутой системы.

2. Объясните, какие удары называются абсолютно упругими, абсолютно неупругими.

3. Сформулируйте закон сохранения импульса.

4. Приведите примеры выполнения и невыполнения закона сохранения импульса.

5. Сформулируйте закон сохранения момента импульса, приведите примеры его выполнения.

6. Дайте определение элементарной работы.

7. Как найти работу силы, действующей на поступательно движущееся тело?

8. Как найти работу силы, действующей на вращательно движущееся тело?

9. Дайте определение мощности, назовите единицы измерения этой физической величины.

10. Как найти мгновенную и среднюю мощность?

11. Какую работу можно считать полезной, полной? Чему равен коэффициент полезного действия машины или механизма?

12. Дайте определение кинетической и потенциальной энергии.

13. Как находится кинетическая энергия тела, катящегося по плоскости без скольжения?

14. Дайте определение консервативных сил.

15. Приведите примеры консервативных и неконсервативных сил.

16. Сформулируйте универсальный закон сохранения энергии и закон сохранения полной механической энергии, приведите примеры их выполнения.

Примеры решения задач

5.1.Частица массы m₁ и импульсом p₁ испытала упругое столкновение с покоившейся частицей массы m₂ (m₁<m₂). Найти импульс 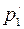первой частицы после столкновения, в результате которого она рассеялась под углом 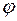к первоначальному направлению движения.

Дано: Найти:

m₁, .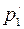

p₁,

m₂,

.

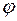Решение:

По закону сохранения импульса

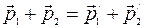, (1)

где 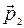=0 – импульс второй частицы до столкновения, 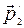- импульс второй частицы после столкновения. Его можно найти по теореме косинусов (рисунок 5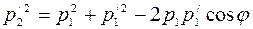.2):

. (2)

С другой стороны, из закона сохранения энергии следует:

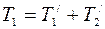, (3)

где 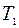- кинетическая энергия первой частицы до столкновения, 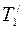и 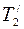- кинетические энергии первой и второй частицы после столкновения. Можно преобразовать равенство (3), с помощью соотношения (5.8), T=p²/2m к виду:

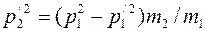. (4)

Исключив 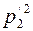из (2) и (4), можно получить:

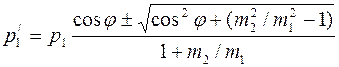. (5)

В выражении (5) физический смысл имеет только знак плюс перед корнем. Это следует из того, что корень будет больше, чем 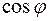, а так как 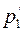- это модуль, то, естественно, он не может быть отрицательным.

Ответ: .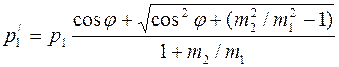

5.2. Камень массы m бросили с поверхности Земли под углом 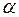к горизонту с начальной скоростью 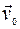. Пренебрегая сопротивлением воздуха, найти мощность силы тяжести через t секунд после начала движения, а также работу этой силы за первые t секунд движения.

Дано: Найти:

M, 1. N,

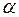, 2. A.

,

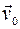t.

Решение:

Скорость камня через t секунд после начала движения 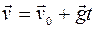. Мощность, развиваемая силой тяжести 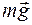в этот момент согласно выражению (5.7) равна:

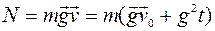. (1)

В нашем случае 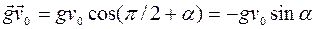, поэтому выражение (1) можно переписать в виде:

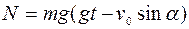. (2)

Работу, совершаемую силой тяжести за первые t секунд движения можно найти по формуле (5.5):

.

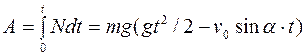Ответ: 1. ,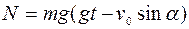

2. .

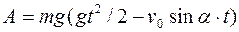5.3.Частица движется по замкнутой траектории в центральном силовом поле, где ее потенциальная энергия U=kr², k – положительная постоянная, r – расстояниечастицы до центра поля О. Найти массу частицы, если наименьшее расстояние ее до точки О равно r₁, аскорость на наибольшем расстоянии от этой точки .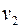

Дано: Найти:

U=kr², m

r₁,

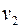
Решение:

Частица имеет на наименьшем расстоянии от точки О момент импульса L₁=mv₁r₁, а на наибольшем – момент импульса L₂=mv₂r₂. Для данного движения частицы применим закон сохранения момента импульса (5.3):

mv₁r₁=mv₂r₂, тогда v₁= v₂r₂/ r₁. (1)

По закону сохранения полной механической энергии:

mv₁²/2 +kr₁²= mv₂²/2+kr₂² . (2)

Решая уравнение (2) относительно m с использованием (1), можно получить:

.

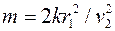Ответ: 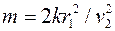.