Линейные неоднородные системы дифференциальных уравнений

Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:

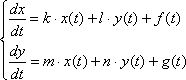По сравнению с однородной системой в каждом уравнении дополнительно добавляется некоторая функция, зависящая от «тэ». Функции 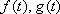могут быть константами (причем, по крайне мере одна из них не равна нулю), экспонентами, синусами, косинусами и т.д.

Например:

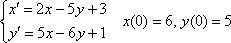
Решение: Дана линейная неоднородная система дифференциальных уравнений, в качестве «добавок» 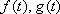выступают константы. Используем метод исключения, при этом сам алгоритм решения полностью сохраняется. Для разнообразия я начну как раз с первого уравнения.

1) Из первого уравнения системы выражаем: 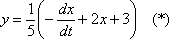из первого уравнения выражается именно «игрек» – через два «икса» и константу.

2) Дифференцируем по обе части:

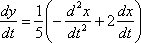
3) Подставим 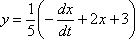и 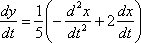во второе уравнение системы 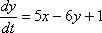, тогда .

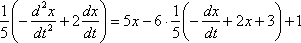Сразу после подстановки целесообразно избавиться от дробей, для этого каждую часть уравнения умножаем на 5:

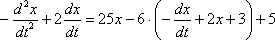Теперь проводим упрощения: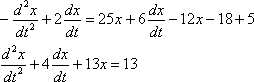

В результате получено линейное неоднородное уравнение второго порядка с постоянными коэффициентами.

Примечание: Тем не менее, в неоднородной системе иногда может получиться и однородное уравнение.

Составим и решим характеристическое уравнение:

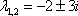– получены сопряженные комплексные корни, поэтому: 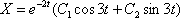Частное решение неоднородного уравнения ищем в виде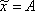

Найдем первую и вторую производную: 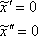. Подставим 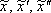в левую часть неоднородного уравнения: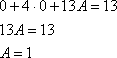

Таким образом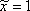

В результате: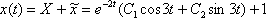

4) Ищем функцию 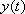. Сначала находим производную от уже найденной функции .

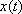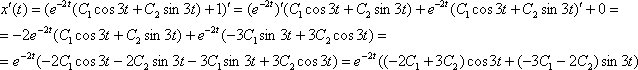
Подставим 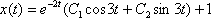и 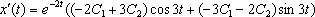в уравнение (*):

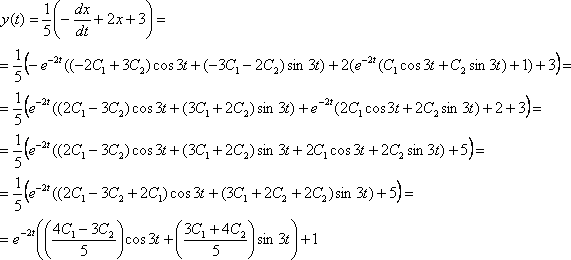
5) Общее решение системы: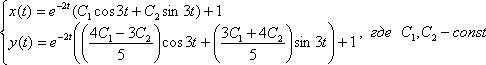

6) Найдем частное решение, соответствующее начальным условиям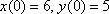

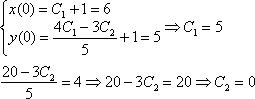
Окончательно, частное решение:

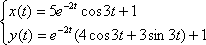
Метод характеристического уравнения (метод Эйлера)

Дана линейная однородная система дифференциальных уравнений

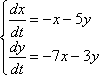
Решение: Смотрим на систему уравнений и составляем определитель второго порядка: 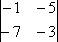Составим характеристическое уравнение, для этого из каждого числа, которое располагается на главной диагонали, вычитаем некоторый параметр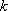

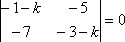Раскрываем определитель: 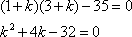И находим корни квадратного уравнения:

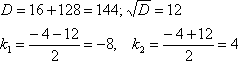
Если характеристическое уравнение имеет два различных действительных корня, то общее решение системы дифференциальных уравнений имеет вид: 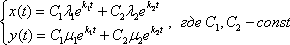Коэффициенты в показателях экспонент 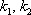нам уже известны, осталось найти коэффициенты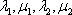

1) Рассмотрим корень 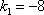и подставим его в характеристическое уравнение:

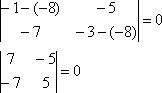Из чисел определителя составим систему двух линейных уравнений с двумя неизвестными: 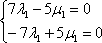Из обоих уравнений следует одно и то же равенство: .

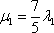Теперь нужно подобрать наименьшее значение 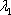, такое, чтобы значение 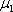было целым.

Очевидно, что следует задать 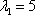. А если 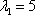то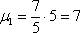

2) Всё аналогично. Рассмотрим корень 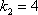и устно подставим его в характеристическое уравнение: 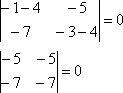Из чисел определителя составим систему: .

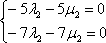Из обоих уравнений следует равенство: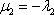

Подбираем наименьшее значение 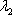, таким образом, чтобы значение 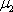было целым.

Очевидно, что .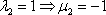

Все четыре коэффициента 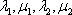найдены, осталось их подставить в общую формулу

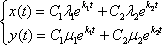
Ответ: общее решение: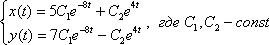

2.Система дифференциальных уравнений 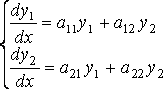где 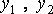- искомые функции от x ; 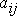- постоянные числа; называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами второго порядка. Систему можно, конечно, решить методом исключения, но можно решить более универсальным методом (методом Эйлера).

Если для вышеуказанной системы известна система линейно независимых частных решений (фундаментальная система решений):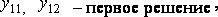

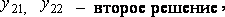
тогда общее решение имеет вид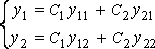

Частные решения ищем в виде : 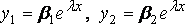После подстановки 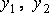в систему и сокращении на 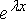получаем систему уравнений для определения неизвестных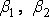 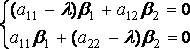Чтобы эта однородная линейная система алгебраических уравнений имела ненулевое решение должно выполняться условие : 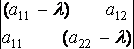- это Уравнение называется характеристическим уравнением, а его корни - характеристическими числами.