A) четырехпроводная звезда
;
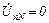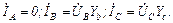
Векторная диаграмма (рис.4.12) демонстрирует работу четырехпроводной системы.
Б) трехпроводная звезда
.
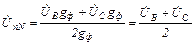Напряжение смещения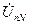 
можно также определить методом засечек, как показано на рис.4.13.
;
;
.
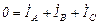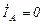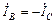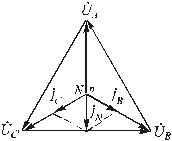
Рис.4.12. Векторная диаграмма для обрыва фазы
в четырехпроводной системе
Токи в фазах b и с должны находиться в противофазе.
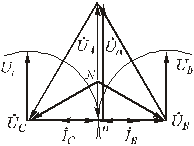
Рис.4.13. Векторная диаграмма для обрыва фазы
в трехпроводной системе
Короткое замыкание фазы
Ra = 0; Rb = Rc;
А) четырехпроводная звезда
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.
Б) трехпроводная звезда
.
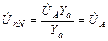Фазные напряжения приемника:
;
;
;
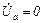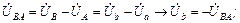
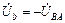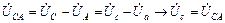т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи фаз:
; 
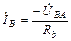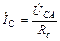увеличились в 
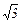раз.
.
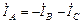Построение векторной диаграммы показано на рис.4.14.
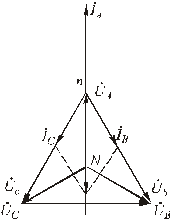
Рис.4.14. Векторная диаграмма для короткого замыкания фазы А
Разнородная нагрузка
А) четырехпроводная звезда
Сравнив схемы соединения потребителей трех- и четырехпроводной звездой, можно сделать вывод, что однофазные приемники надо включать по схеме четырехпроводной звезды, чтобы обеспечить постоянство напряжений на зажимах этих приемников.
По схеме трехпроводной звезды включают трехфазные симметричные приемники, например, трехфазные асинхронные и синхронные двигатели.
4.3.2. Соединение потребителей «треугольником»
Рассмотрим различные режимы работы приемника при соединении его фаз треугольником.
Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).
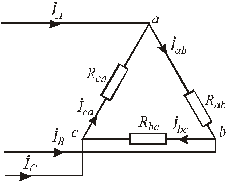
Рис.4.15. Соединение фаз приемника «треугольником»
А) симметричный режим.
Rab = Rbc = Rca = Rф.
На рис.4.7 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника «треугольником».
Токи равны по модулю и отличаются только по фазе:
.
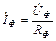Линейные токи:
;
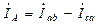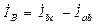; 98(4.9)
;
.
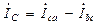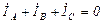в) несимметричные режим.
Rab ¹ Rbc = Rca;
Фазы по-прежнему работают независимо друг от друга и поэтому фазные токи:
; 
; 
;
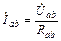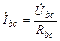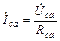Линейные токи определяются соответственно по формулам (4.9). На рис.4.16 представлены векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
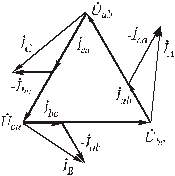
Рис.4.16. Векторные диаграммы для несимметричной нагрузки приемников соединенных «треугольником».
С) обрыв фазы.
Rab = ¥ ; Rbc = Rca .
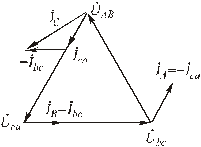
Рис.4.17. Векторная диаграмма для обрыва фазы при
соединении приемников треугольником
;
;
.
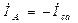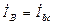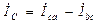При разнородной нагрузке методика расчета не меняется.
Мощность трехфазной цепи
Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, то имеем:
;
;
.
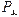
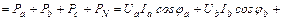
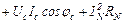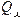
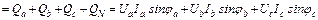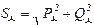При симметричной нагрузке для трех- и четырехпроводной системы:
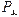
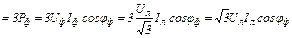;99(4.10)
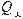
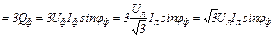;100(4.11)
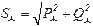
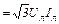. 101(4.12)
При соединении фаз приемника треугольником и несимметрии нагрузки имеем:
;
;
.
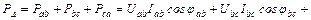
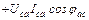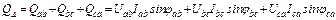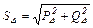При симметричной нагрузке:
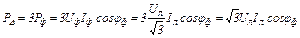; 102(4.13)
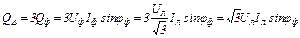; 103(4.14)
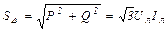. 104(4.15)
При этом необходимо учесть, что одинаковые формулы для подсчета мощности не означают одинаковые численные значения.
Пример. Пусть трехфазный приемник с сопротивлением фазы Zф соединен «звездой», тогда активная мощность
.
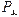
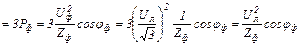Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трехфазному источнику:
,
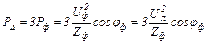т.е.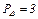 
.
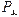