Точечная оценка параметров генеральной совокупности

Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Это функция результатов выборки, и она является точечной оценкой генерального параметра, т. е. принимает только одно значение.

Качество оценки устанавливается по трем свойствам: быть состоятельной, эффективной и несмещенной.

Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.

Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.

Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя :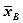

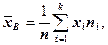
где 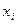- варианты выборки; 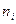- частота встречаемости вариант 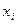; n - объем выборки.

Выборочная средняя является несмещенной оценкой генеральной средней, так как 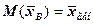,т.е. она эквивалентна истинной средней в генеральной совокупности (популяции).

Выборочная дисперсия 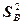не обладает свойством несмещенности. Это смещенная оценка генеральной дисперсии .

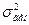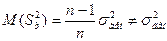- это и означает, что выборочная дисперсия 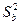является смещенной оценкой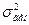

На практике используют исправленную выборочную дисперсию 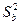, которая является несмещенной оценкой дисперсии генеральной совокупности:

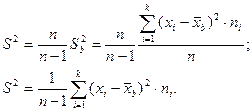
Кроме того, в расчетах используют S - исправленное среднее квадратическое отклонение, называемое стандартным отклонением в выборке и ошибку выборочной средней

(стандартную ошибку средней) :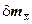

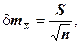которая отражает точность оценки.

Стандартная ошибка уменьшится, т. е. оценка станет более точной, если объем выборки n увеличится и данные имеют небольшое рассеяние S.

Рассмотрим разницу между S - стандартным отклонением в выборке и 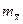- стандартной ошибкой среднего.

На первый взгляд, они очень схожи, но их используют в разных целях. Среднее квадратическое отклонение S отражает вариабельность в значениях данных, и его указывают, если надо пояснить изменчивость в наборе данных, разброс данных.

Ошибка выборочной средней 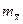характеризует точность выборочного среднего 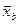и должна быть указана, если интерес представляет среднее значение выборки.

Из генеральной совокупности извлечена выборка объема n=50.

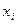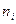Найти несмещенную оценку генеральной средней.

Решение:

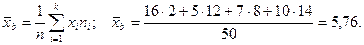
По выборке объема 30 найдена смещенная оценка 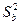= 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.

Решение:

Эта несмещенная оценка равна исправленной дисперсии:

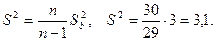
Найти несмещенную оценку генеральной средней, дисперсии генеральной совокупности и стандартное отклонение по выборке объема 12, описывающую продолжительность в секундах физической нагрузки до развития приступа стенокардии:

289,203,359,243,232,210,251,251,246,224,239,220,211.

Решение:

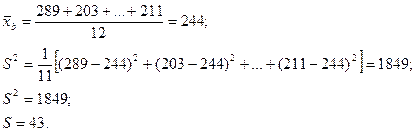
Варианты заданий

№ 13.1. При исследовании клинической оценки тяжести серповидноклеточной анемии была получена выборка объема 33.

0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 4; 4; 5;

5;5;5;6;7;9;10;11.

Найдите среднюю, среднее квадртическое отклонение и

медиану. Можно ли считать, что выборка извлечена из

совокупности с нормальным распределением?

№ 13.2. Исследуя продолжительность (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца, получили следующие данные:

289;203; 359; 243; 232; 210; 215; 246; 224; 239; 220; 211. Найдите среднюю, среднее квадратическое отклонение, медиану. Можно ли считать, что данная выборка извлечена из совокупности с нормальным распределением?

№ 13.3. Найдите среднее число очков, выпадающих при бросании игральной кости. Опишите это распределение. Может ли оно быть нормальным?