Нестационарный пуассоновский поток
Если поток событий нестационарен, то его основной характеристикой является мгновенная плотность λ(t). Мгновенной плотностью потока называется предел отношения среднего числа событий, приходящегося на элементарный участок времени (t, t + ∆t), к длине этого участка, когда последняя стремится к нулю:
λ(t) = 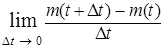 = m′(t),
= m′(t),
где m(t) – математическое ожидание числа событий на участке (0, t). В дальнейшем для однородности изложения будем величину λ(t) называть интенсивностью.
Рассмотрим поток однородных событий, ординарный и без последействия, но не стационарный, с интенсивностью λ(t), некоторый промежуток времени длиной τ > 0, начинающийся с момента t0 (и заканчивающийся, следовательно, в момент t0 + τ) и дискретную случайную величину Х(t0, τ) – число событий, наступающих в потоке за промежуток времени от t0 до t0 + τ.
Теорема 1. В нестационарном пуассоновском потоке с интенсивностью λ(t):
1) Случайная величина Х(t0, τ) распределена по закону Пуассона
Рm(t0, τ) = 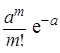 , (m = 1, 2, …),
, (m = 1, 2, …),
где Рm(t0, τ) – вероятность того, что за промежуток времени [t0, t0 + τ] в потоке наступит ровно m событий, а параметр а – математическое ожидание числа событий на участке от t0 до t0 + τ, равное
а = 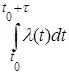 ;
;
2) Дисперсия случайной величины Х(t0, τ)
D(Х(t0, τ)) = a.
Из этой теоремы существует ряд следствий, которые, так же, как и в предыдущем параграфе, несколько позже сведем в единую таблицу.
Определение. Элементом вероятности появления события в нестационарном пуассоновском потоке называется вероятность p1(t0; Δt) появления события за элементарный (достаточно малый) промежуток времени от t0 до t0 + Δt.
Разница в определениях элемента вероятности для простейшего и нестационарного потоков состоит в том, что во нестационарном потоке элемент вероятности зависит не только от длины промежутка Δt, как в случае простейшего потока, но и от его начала t0.
Теорема 2. Для элемента вероятности появления события за элементарный промежуток времени от t0 до t0 + Δt в нестационарном пуассоновском потоке с интенсивностью λ(t) имеет место приближенная формула
p1(t0; Δt) ≈ λ(t0) ∙ Δt (Δt → 0).
Теперь приведем таблицу, аналогичную таблице предыдущего параграфа.
Характеристики случайной величины Х(t0, τ).
|
| Характеристика | Формула | |
| Интенсивность нестационарного пуассоновского потока | λ(t) | |
| Математическое ожидание случайной величины Х(t0, τ) | а =a(t0, τ) = M(Х(t0, τ)) = 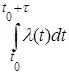 | |
| Закон распределения Пуассона случайной величины Х(t0, τ) | Рm(t0, τ) = 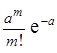 , (m = 1, 2, …) , (m = 1, 2, …) | |
| Вероятность того, что за промежуток времени от t0 до t0 + τ не наступит ни одного события | p0(t0,t0 + τ) = Р(Х(t0, τ)= 0) = 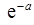 | |
| Вероятность того, что за промежуток времени от t0 до t0 + τ наступит менееk (k=1,2,3…) событий | Р(Х(t0, τ)<k) = 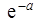 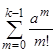 | |
| Вероятность того, что за промежуток времени от t0 до t0 + τ наступит неменееk (k=1,2,3…) событий | Р(Х(t0, τ) ≥ k) = 1- 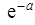 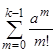 | |
| Вероятность того, что за промежуток времениот t0 до t0 + τ наступит хотя бы одно событие | Р(Х(t0, τ) ≥ 1) = 1 - 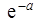 | |
| Элемент вероятности появления события за элементарный промежуток времени от t0 до t0+ Δt | p1(t0; Δt) ≈ λ(t0) ∙ Δt (Δt → 0). | |
| Дисперсия случайной величины Х(t0, τ) | D(Х(t0, τ)) = а | |
| Среднее квадратическое отклонение случайной величины Х(t0, τ) | σ(Х(t0, τ)) = 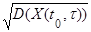 = = 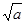 |
Найдем для нестационарного потока закон распределения промежутка времени между соседними событиями. Ввиду нестационарности потока, этот закон будет зависеть от того, где на оси 0t будет расположено первое из событий. Кроме того, он будет зависеть от вида функции λ(t). Предположим, что первое из двух соседних событий появилось в момент времени t0, и найдем при этом условии закон распределения времени Т(t0) между этим событием и последующим
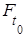 (t) = P(T < t) = 1 – P(T ≥ t).
(t) = P(T < t) = 1 – P(T ≥ t).
Найдем P(T ≥ t) – вероятность того, что на участке от t0 до t0 + t не появится ни одного события
P(Т(t0) ≥ t) = ℮- а = 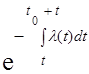 , (1)
, (1)
откуда
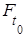 (t) = 1 -
(t) = 1 - 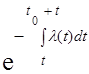 .
.
Дифференцируя, найдем плотность распределения
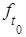 (t) = λ(t0 + t)
(t) = λ(t0 + t) 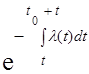 (t > 0) .
(t > 0) .
Этот закон распределения уже не будет показательным. Вид его зависит от t0 и вида функции λ(t).
Несмотря на то, что структура нестационарного пуассоновского потока несколько сложнее, чем простейшего, он очень удобен в практических применениях: главное свойство простейшего потока – отсутствие последействия – в нем сохранено.
Потоки Пальма и Эрланга.
Обобщением простейшего потока в другом направлении, чем нестационарный пуассоновский поток, является поток с ограниченным последействием.
Рассмотрим ординарный поток однородных событий. Этот поток называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательными событиями Т1, Т2, … представляют собой независимые случайные величины.
Примеры потоков Пальма:
1) Некоторая деталь технического устройства работает непрерывно до своего отказа, после чего мгновенно заменяется новой. Срок безотказной работы детали случаен; отдельные экземпляры выходят из строя независимо друг от друга. При этих условиях поток отказов (или поток «восстановлений) представляет собой поток Пальма. Если к тому же срок работы детали распределен по показательному закону, то поток Пальма превращается в простейший.
2) Группа самолетов идет в боевом порядке «колонна» (друг за другом в одну линию) с одинаковой для всех самолетов скоростью V. Каждый самолет, кроме ведущего, должен выдерживать строй, т.е. держаться на заданном расстоянии L от впереди идущего. Это расстояние, вследствие погрешности приборов, выдерживается с ошибками. Моменты пересечения самолетами заданного рубежа образуют поток Пальма, так как случайные величины Т1 = 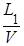 , Т2 =
, Т2 = 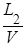 , … независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.
, … независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.
Потоки Пальма часто получаются в виде выходных потоков СМО. Основной в теории выходных потоков является следующая теорема.
Теорема (Пальма). Пусть на СМО поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ (не обслуживается). Если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок является также потоком Пальма.
В частности, если входной поток заявок будет простейшим, то поток необслуженных заявок, не будучи простейшим, будет все-таки иметь ограниченное последействие.
Одним из из важных примеров потоков с ограниченным последействием являются так называемые потоки Эрланга, которые образуются «просеиванием» простейшего потока.
Рассмотрим простейший поток и выбросим из него каждую вторую точку (на рисунке выброшенные точки отмечены крестиками).
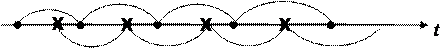 |
Оставшиеся точки образуют поток, который называется потоком Эрланга первого порядка (Э1). Очевидно, этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то независимы и величины Т1, Т2, …, получающиеся суммированием таких промежутков по два.
Процесс выбрасывания точек из простейшего потока можно продолжить и тогда поток, получаемый из простейшего сохранением каждой (k+1)-й точки и выбрасыванием всех остальных, называется потоком Эрланга k-го порядка (Эk).
Найдем закон распределения промежутка времени Т между соседними событиями в потоке Эрланга k-го порядка. Рассмотрим на оси 0t простейший поток с интервалами Т1, Т2, …. Величина Т представляет собой сумму k+1 независимых случайных величин
Т = 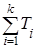 ,
,
где Т1, Т2, … Тk – независимые случайные величины, подчиненные одному и тому же показательному закону
f(t) = λ℮-λt (t > 0). (1)
|
 Обозначим fk(t) плотность распределения величины Т для потока Эk. Тогда fk(t)dt есть вероятность того, что величина Т примет значение между t и dt.
Обозначим fk(t) плотность распределения величины Т для потока Эk. Тогда fk(t)dt есть вероятность того, что величина Т примет значение между t и dt. 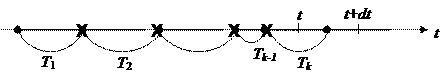 |
Это означает, что последняя точка промежутка Т должна попасть на элементарный участок (t, t+dt), а предыдущие k-1 точек простейшего потока – на участок (0, t). Вероятность первого события равна λdt; вероятность второго по закону Пуассона будет
pk(t) = 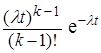 .
.
Перемножая эти вероятности, получим
fk(t)dt = λ 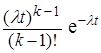 dt,
dt,
откуда
fk(t) = 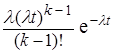 (t > 0).
(t > 0).
Закон распределения с полученной плотностью называется законом Эрланга k-го порядка. Очевидно, что при k = 1 он обращается в показательный (1).
Найдем характеристики потока Эрланга fk(t) – математическое ожидание mk и дисперсию Dk. По теореме сложения математических ожиданий
mk = 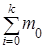 = km0,
= km0,
где m0 = 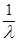 – математическое ожидание промежутка между событиями в простейшем потоке. Отсюда
– математическое ожидание промежутка между событиями в простейшем потоке. Отсюда
mk = 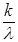 .
.
Аналогично по теореме сложения дисперсий
Dk = 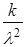 , σk =
, σk = 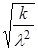 .
.
Обозначим через λk интенсивность потока Эрланга k-го порядка (среднее число событий потока Эk в единицу времени). Тогда λk = 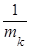 и, следовательно,
и, следовательно,
λk = 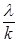 или λ = kλk.
или λ = kλk.
Таким образом, интенсивность λk потока Эрланга k-го порядка в k раз меньше интенсивности λ исходного простейшего потока.
Уменьшение интенсивности потока Эрланга k-го порядка при увеличении его порядка создает определенное неудобство при использовании потоков Эk. Чтобы интенсивность λk при увеличении k оставалась постоянной, равной интенсивности λ исходного простейшего потока, достаточно уменьшить в k раз масштаб по временной оси 0t, т.е. уменьшить в k раз промежуток времени Т между соседними событиями потока Эk. Образованный таким образом поток называется нормированным потоком Эрланга k-го порядка и обозначается 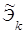 .
.
Для потока 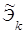 имеем:
имеем:
1) Интенсивность потока 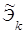 равна
равна 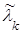 = kλk = λ, k = 1,2.3,…
= kλk = λ, k = 1,2.3,…
2) Промежуток времени между любыми двумя соседними событиями потока 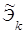 равен
равен 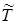 =
= 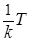 , k = 1,2.3,….
, k = 1,2.3,….
3) Математическое ожидание случайной величины 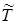 равно
равно
М( 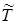 ) =
) = 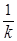 mk =
mk = 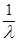 , k = 1,2.3,….
, k = 1,2.3,….
4) Дисперсия случайной величины 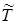 равна
равна
D( 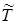 ) =
) = 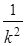 Dk =
Dk = 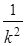
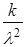 =
= 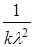 , k = 1,2.3,….
, k = 1,2.3,….
5) Среднее квадратическое отклонение случайной величины 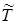 равно
равно
σ( 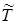 ) =
) = 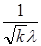 , k = 1,2.3,….
, k = 1,2.3,….
Таким образом, приходим к выводу: при неограниченном увеличении k нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными 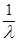 .
.
Это свойство потоков Эрланга удобно в практических применениях; оно дает возможность, задаваясь различными k, получить любую степень последействия: от полного отсутствия (k = 1) до жесткой функциональной связи между моментами появления событий (k = ∞). В целях упрощения бывает удобно заменить реальный поток заявок, имеющий последействие, нормированным потоком Эрланга с примерно такими же характеристиками промежутка между заявками – математическим ожиданием и дисперсией.
Пример. В результате статистической обработки промежутков между заявками в потоке получены оценки для математического ожидания и дисперсии величины Т:
mt = 2 (мин), Dt = 0,8 (мин2).
Заменить этот поток нормированным потоком Эрланга с теми же характеристиками.
Решение. Имеем λ = 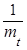 = 0,5.
= 0,5.
Из формулы дисперсии получаем k ≈ 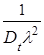 =
= 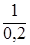 = 5.
= 5.
Таким образом, поток можно приближено заменить нормированным потоком Эрланга пятого порядка.
Полученные характеристики случайных величин Т для потока Эрланга k-того порядка Эk и 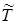 =
= 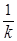 Т для нормированного потока Эрланга k-того порядка
Т для нормированного потока Эрланга k-того порядка 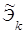 сведем в единую таблицу.
сведем в единую таблицу.
|
| № | Характеристики случайных величин | Случайные величины | |
| Т – промежуток времени между любыми двумя соседними событиями в потоке Эрланга k-того порядка Эk | 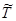 - промежуток времени между любыми двумя соседними событиями в нормированном потоке Эрланга k-того порядка - промежуток времени между любыми двумя соседними событиями в нормированном потоке Эрланга k-того порядка 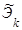 | ||
| Интенсивность исходного простейшего потока | λ | λ | |
| Интенсивность потока Эрланга k-того порядка | λk | 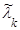 = kλk = λ = kλk = λ | |
| Плотность распределения | fk(t) = 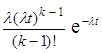 | 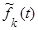 =k fk(kt) = =k fk(kt) = 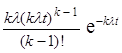 | |
| Параметр закона распределения | λ = kλk | kλ | |
| Математическое ожидание | М(Т) = 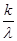 = = 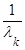 | М( 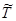 ) = ) = 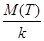 = = 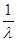 | |
| Дисперсия | D(Т) = 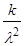 = = 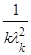 | D( 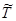 ) = ) = 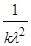 | |
| Среднее квадратическое отклонение | σ(T) = 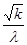 = = 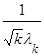 | σ ( 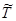 ) = ) = 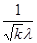 |
Решение типовых задач

1. Помогите управляющему нового ресторана быстрого питания описать количественно процесс поступления посетителей, оценивая долю интервалов времени между их приходами, которые будут
1) Меньше двух минут.
2) Больше трех минут.
Интенсивность поступления посетителей в рестораны подобного типа равна 35 клиентов в час. Время между приходами последовательных посетителей распределено по экспоненциальному закону.
Решение. 1) 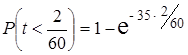 =
= 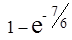 ≈ 0,6886.
≈ 0,6886.
2) 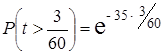 =
= 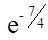 ≈ 0,1738.►
≈ 0,1738.►

2. Посетитель ресторана быстрого питания, который приходит в пределах четырехминутного интервала после предыдущего посетителя, обслуживается без очереди. Если же время между последовательными приходами посетителей составляет о 4 до 5 минут, время ожидания будет около 1 минуты. Если время между последовательными приходами посетителей составляет более 5 минут, время ожидания составляет около 2 минут. Время между последовательными приходами посетителей распределено по экспоненциальному закону со средним значением 6 минут.
1) Определите вероятность того, что прибывающий посетитель не будет ожидать в очереди.
2) Определите среднее время ожидания для прибывающего посетителя.
Решение. М(Х) = 6 минут, следовательно, λ = 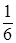 посетителя в минуту.
посетителя в минуту.
1) Промежуток времени – 4 минуты, нужно вычислить вероятность того, что клиент прибудет. Поэтому
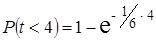 =
= 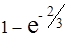 ≈ 0,4883.
≈ 0,4883.
2) Вероятность того, что время между последовательными приходами посетителей составит от 4 до 5 минут, равно приращению функции распределения на этом промежутке, т.е.
F(5) – F(4) = 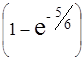 -
- 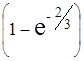 =
= 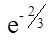 -
- 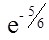 ≈ 0,5117 – 0,4361 = 0,075.
≈ 0,5117 – 0,4361 = 0,075.
Вероятность того, что время между последовательными приходами посетителей составит более 5 минут, равно
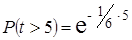 ≈ 0,4361.
≈ 0,4361.
Следовательно, среднее время ожидания для посетителя составит
1·0,075 + 2·0,4361 = 0,9472 минуты. ►
 3. Для анализа изменения с течением времени размера текущего фонда компании, ведущей дела по автострахованию, важно обладать информацией о процессе поступлений в компанию требований по выплатам в соответствии со страховыми полисами.
3. Для анализа изменения с течением времени размера текущего фонда компании, ведущей дела по автострахованию, важно обладать информацией о процессе поступлений в компанию требований по выплатам в соответствии со страховыми полисами.
Наблюдение за работой компании в предшествующий период показало, что число поступающих в компанию требований по выплатам за любой промежуток времени длиной τ не зависит от момента времени, с которого начинается отсчет промежутка τ, а зависит только от его продолжительности; требования в компанию в любые два непересекающиеся интервалы времени поступают независимо; в достаточно малые промежутки времени в компанию поступает по одному требованию. Ожидаемое число требований, поступающих в компанию за месяц, равно 6.
Какова вероятность того, что:
1) за месяц в компанию поступит 7 требований;
2) за месяц в компанию поступит менее 7 требований;
3) за месяц в компанию поступит не менее 7 требований;
4) за неделю в компанию не поступит ни одного требования;
5) за две недели в компанию поступит хотя бы одно требование;
6) интервал времени между двумя соседними требованиями будет менее двух дней;
6) интервал времени между двумя соседними требованиями будет не менее двух дней.
Ответ. Временная единица – 1 месяц
p7(1) ≈ 0,138;
Р(Х(1) < 7) ≈ 0,606;
Р(Х(1) ≥ 7) ≈ 0,394;
p0( 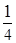 ) ≈ 0,223;
) ≈ 0,223;
Р(Х( 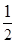 ) ≥ 1) ≈ 0,950;
) ≥ 1) ≈ 0,950;
P(T < 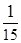 ) ≈ 0,670;
) ≈ 0,670;
P(T ≥ 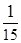 ) ≈ 0,330.►
) ≈ 0,330.►
 4. Для страховой компании, занимающейся автострахованием, проанализировать поток поступлений требований по выплатам в соответствии со страховыми полисами за период с начала ноября по конец января. Изучение этого потока в рассматриваемый период в прошлые годы показало, что число требований по выплатам, поступающих за некоторый промежуток времени τ, зависит не только от его продолжительности, но и от его начала. Объясняется это тем, что в рассматриваемый период ухудшаются погодные условия, обстановка на дорогах, что ведет к увеличению дорожно-транспортных происшествий.
4. Для страховой компании, занимающейся автострахованием, проанализировать поток поступлений требований по выплатам в соответствии со страховыми полисами за период с начала ноября по конец января. Изучение этого потока в рассматриваемый период в прошлые годы показало, что число требований по выплатам, поступающих за некоторый промежуток времени τ, зависит не только от его продолжительности, но и от его начала. Объясняется это тем, что в рассматриваемый период ухудшаются погодные условия, обстановка на дорогах, что ведет к увеличению дорожно-транспортных происшествий.
Независимость поступлений требований в любые непересекающиеся интервалы времени и поступление требований по одному в малые промежутки времени сохраняются и в данной ситуации.
Ожидаемое число требований, поступающих в компанию за неделю, зависит от времени следующим образом: λ(t) = 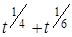 .
.
С какой вероятностью
1) за ноябрь месяц поступит в компанию 6 требований;
2) за декабрь месяц поступит в компанию 6 требований;
3) за январь месяц поступит в компанию не менее 5 требований;
4) за первые две недели ноября не поступит ни одного требования;
5) за вторую и третью недели декабря поступит хотя бы одно требование;
6) интервал времени между двумя соседними поступлениями требований будет не менее трех дней, если первое из них поступило в первый день второй недели января;
7) интервал времени между двумя соседними поступлениями требований будет менее двух дней, если первое из них поступило в первый день третьей недели декабря.
Ответ. За единицу времени принять неделю.
Р6(0; 4) ≈ 0,072;
Р6(4; 4) ≈ 0,005;
Р(Х(8,4) ≥ 5) ≈ 0,999;
p0(0,2) ≈ 0,022;
Р(Х(5,2) ≥ 1) ≈ 0,999;
P(T(9) ≥ 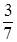 ) ≈ 0,147;
) ≈ 0,147;
P(T(6) < 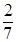 ) ≈ 0,665.►
) ≈ 0,665.►
 5. Туристическая фирма формирует группы для туристических поездок. Отправления групп осуществляется по мере их формирования. Статистическая обработка интервала времени между отправлениями групп дала следующие результаты: средний интервал времени между отправлениями двух соседних групп 2,5 (недели), дисперсия интервала между отправлениями двух соседних групп 2,7 (недели2).
5. Туристическая фирма формирует группы для туристических поездок. Отправления групп осуществляется по мере их формирования. Статистическая обработка интервала времени между отправлениями групп дала следующие результаты: средний интервал времени между отправлениями двух соседних групп 2,5 (недели), дисперсия интервала между отправлениями двух соседних групп 2,7 (недели2).
Требуется заменить поток отправлений групп нормированным потоком Эрланга 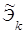 , обладающим приближенно теми же характеристиками, найти его интенсивность
, обладающим приближенно теми же характеристиками, найти его интенсивность 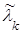 , порядок k и плотность распределения
, порядок k и плотность распределения 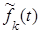 . Исследовать функцию плотности и построить ее график. Найти вероятность того, что интервал между двумя соседними отправлениями туристических групп будет больше одной и меньше двух недель.
. Исследовать функцию плотности и построить ее график. Найти вероятность того, что интервал между двумя соседними отправлениями туристических групп будет больше одной и меньше двух недель.
Ответ. k = 2; 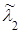 = 0,4 (отправления в неделю)
= 0,4 (отправления в неделю)
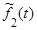 = 0,64∙t∙℮-0,8t;
= 0,64∙t∙℮-0,8t; 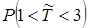 ≈ 0,5.►
≈ 0,5.►
