Эквивалентные преобразования активных треугольника и звезды.

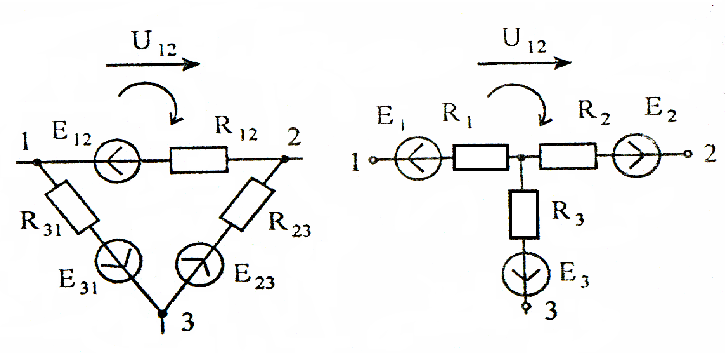
Рисунок 15

При преобразовании треугольник – звезда в ветвях эквивалентной звезды содержатся как пассивные элементы (сопротивления), так и активные (источники ЭДС). Величины эквивалентных ЭДС определяют из условия равенства разности потенциалов между соответствующими узлами до и после преобразования при полном отключении преобразуемого участка от остальной части цепи (рисунок 15). В этом случае во всех ветвях треугольника течёт ток, а в ветвях звезды токи отсутствуют.

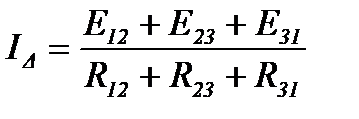(11)

Запишем второй закон Кирхгофа для ветви R₁₂ , E₁₂треугольника:

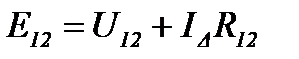
и для звезды

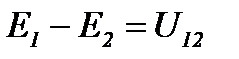
Поскольку величины напряжений U₁₂ в обеих схемах должны быть одинаковыми, получим

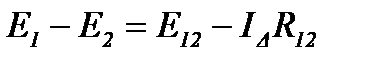(12)

Аналогично для остальных ветвей имеем

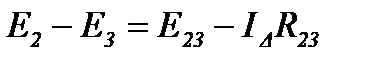(13)

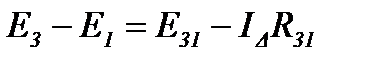(14)

Выражения (11) – (14) дают возможность определять величины эквивалентных ЭДС.

При переходе от треугольника к эквивалентной звезде с целью упрощения решаемой задачи величина ЭДС в одной из ветвей звезды может быть выбрана произвольно. Пусть, например, Е₃ = 0, тогда из выражений (13), (14) получим:

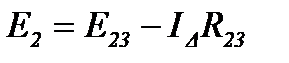
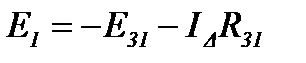
При переходе от звезды кэквивалентному треугольнику в качестве дополнительного условия можно принять

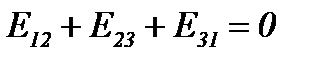
Тогда 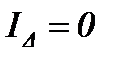и из выражений (12) - (14) получим

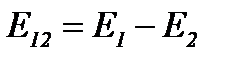
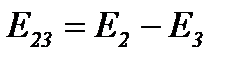
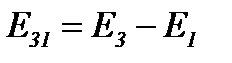
Величины эквивалентных сопротивлений звезды и треугольника определяются по формулам (1)-(6). Рассмотрим, например схему Рисунок 16, которая при помощи преобразования звезды с ветвями (R₁, Е₁), (R₂, E₂), (R₃, Е₃) в эквивалентный треугольник получает вид рисунок 17.

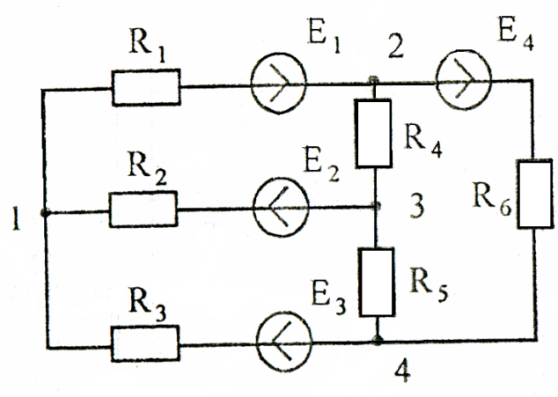
Рисунок 16

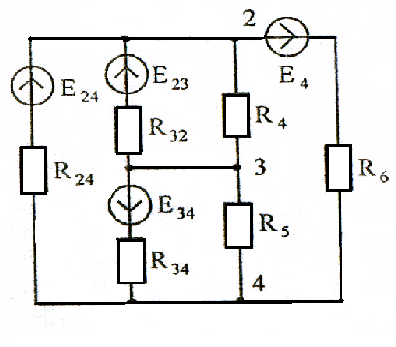
Рисунок 17

Выберем в качестве дополнительного условия

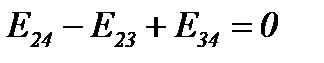
Тогда

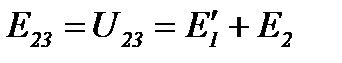
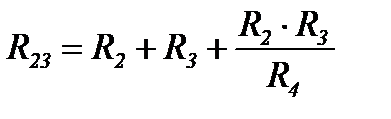
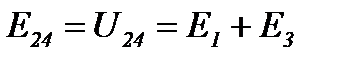
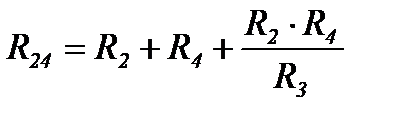
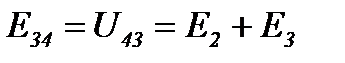
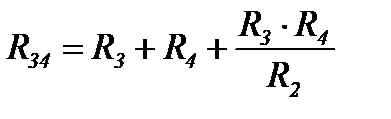
Рассмотрим преобразование треугольника 1 2 3 (рисунок 16) в эквивалентную звезду, для чего выделим его из цепи (рисунок 18а).

Ток треугольника

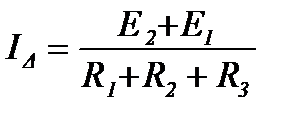
Напряжения между узлами треугольника и звезды:

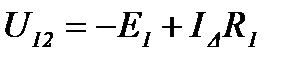
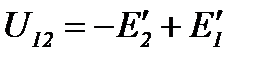
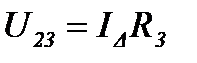
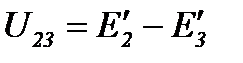
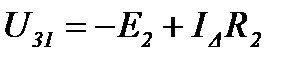
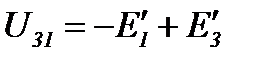
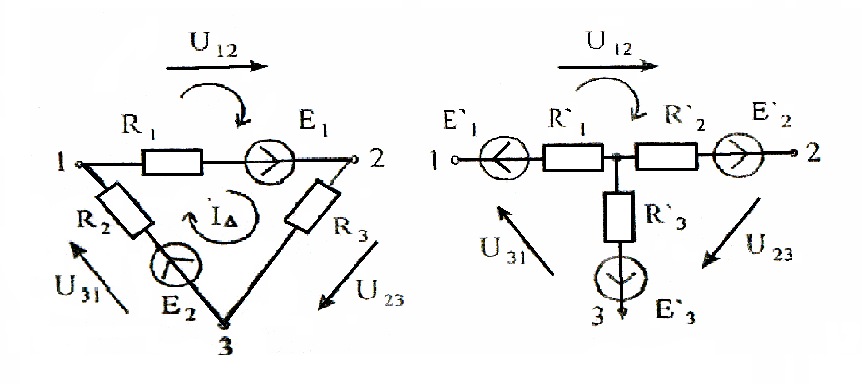
а) б)

Рисунок 18

Принимаем для упрощения 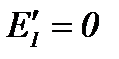, тогда:

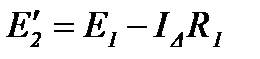
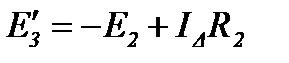
В итоге схема (рисунок 16) принимает вид, представленный на рисунке 19.

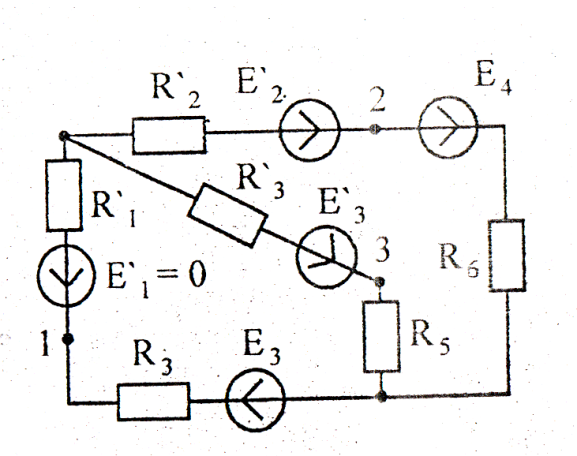
Рисунок 19

Задача 1

Определить эквивалентное сопротивление R_Э (рисунок 20, 21, 22) относительно указанных зажимов, если сопротивления равны 10 Ом. Данные взять из табл. 1-3 (номер варианта соответствует порядковому номеру студента в журнале, номеру 11 соответствует 1 вариант).

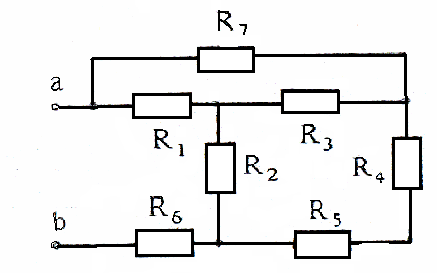
Рисунок 20

Таблица 1.

№
	R7=0	R4=∞	R3=∞	R1=0	R1=∞	R2=0	R2=∞	R7=0	R4=0 R5=0	R7=∞

Таблица 1

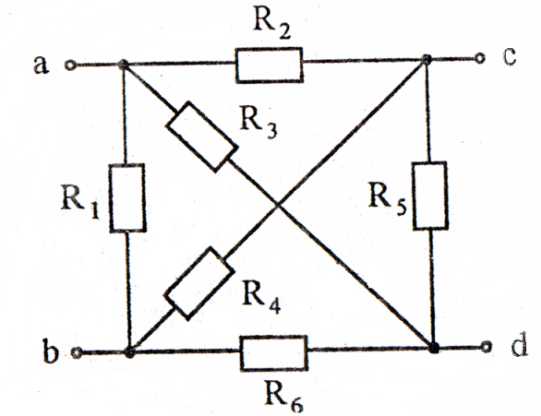
Рисунок 21

Таблица 2

№
	R5=0	R5=∞	R4=0	R3=0	R3=0	R1=∞	R5=0	R2=0	R4=0	R2=0
?	Rab	Rab	Rab	Rcd	Rac	Rbd	Rac	Rcd	Rad	Rbc

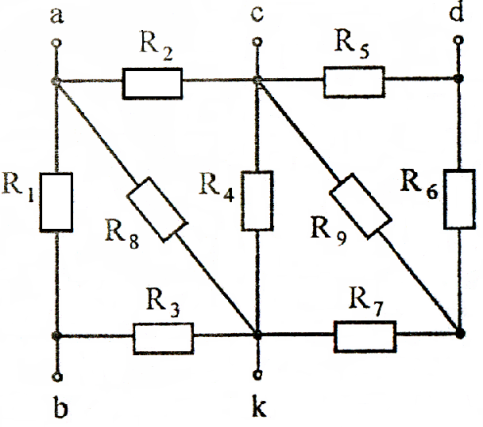
Рисунок 22

Таблица 3

№
	R9=0	R4=∞	R7=∞	R8=0	R8=0 R9=0	R8=0 R9=∞	R8=0	R2=0 R7=0	R6=∞	R3=∞ R8=0
?	Rab	Rab	Rab	Rcd	Rac	Rkd	Rcd	Rcb	Rck	Rak

Задача 2

Используя преобразования параллельных ветвей, упростить схему до трёхконтурной. Составить уравнения по законам Кирхгофа для эквивалентной схемы. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема).

Схемы к задаче 2:

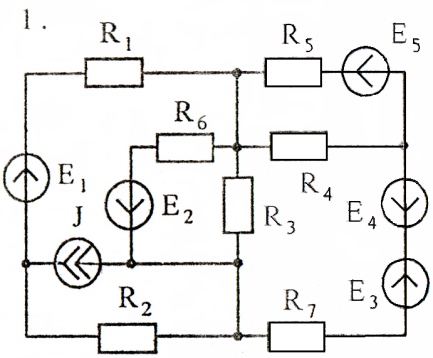
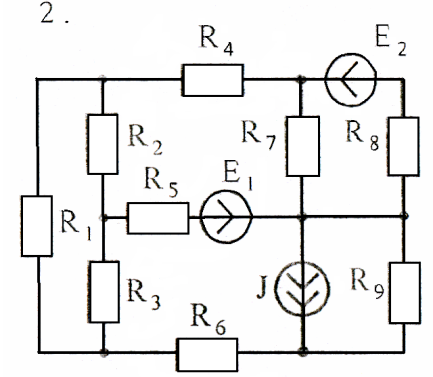
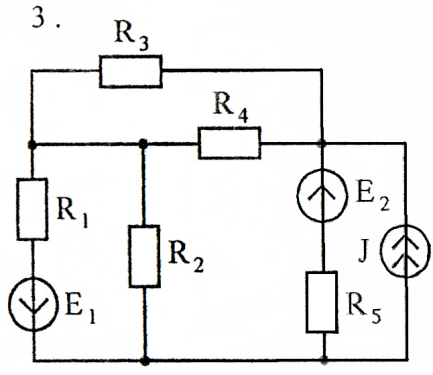
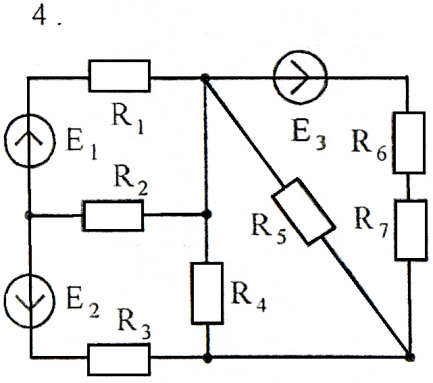
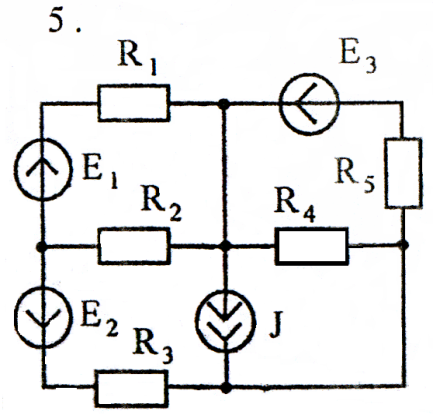
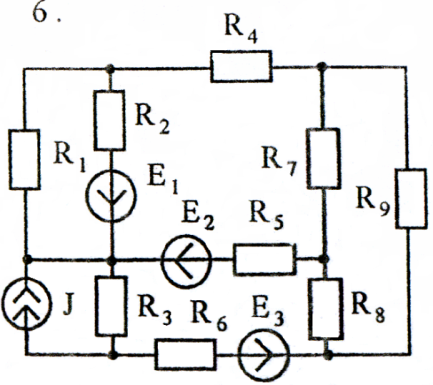
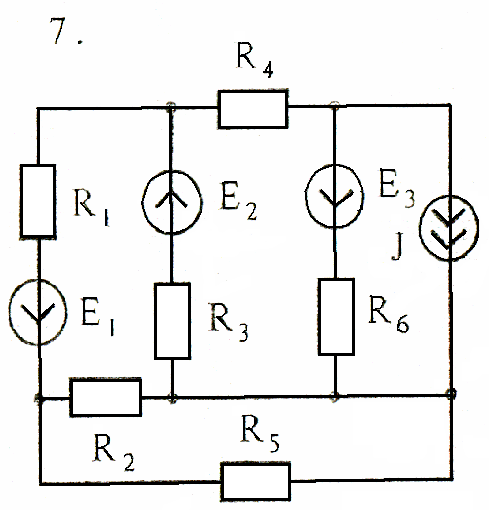
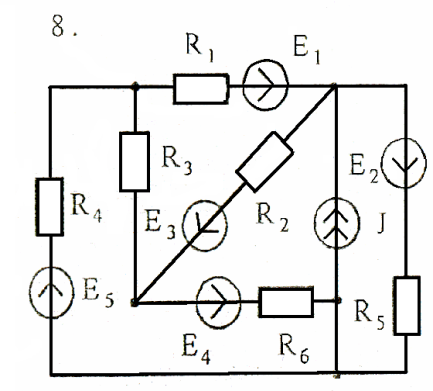
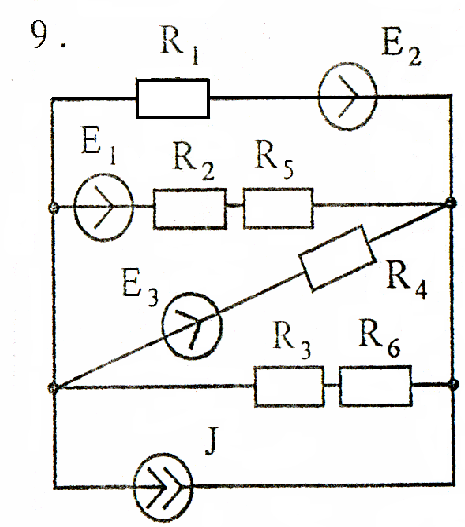
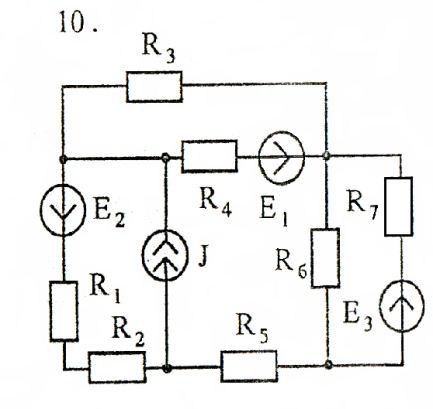
Задача 3

Используя взаимные преобразования активных треугольника и звезды, упростить схему до трёхконтурной. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема).

Схемы к задаче 3:

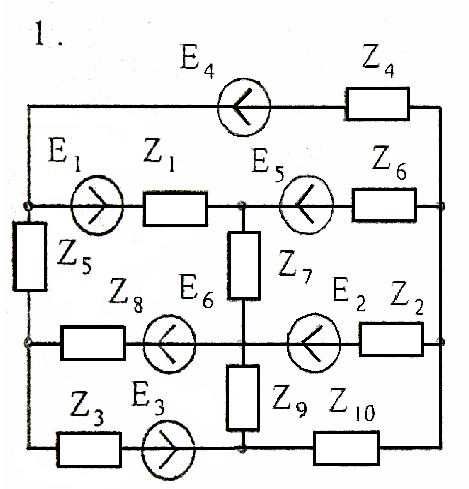
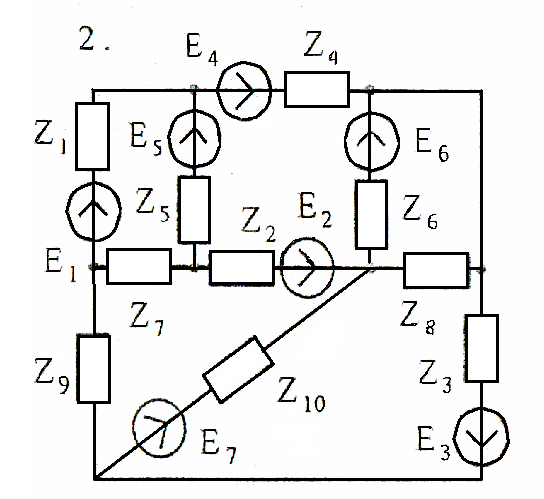
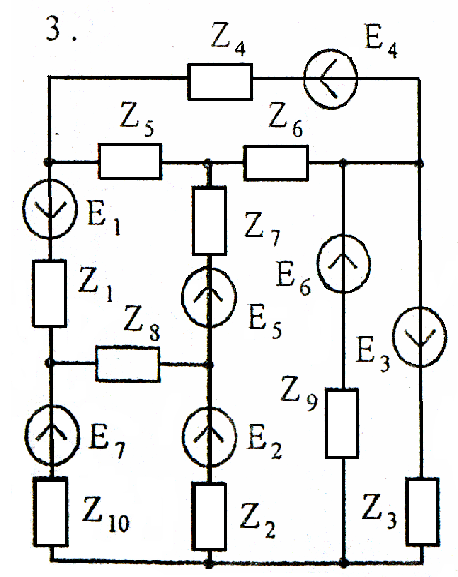
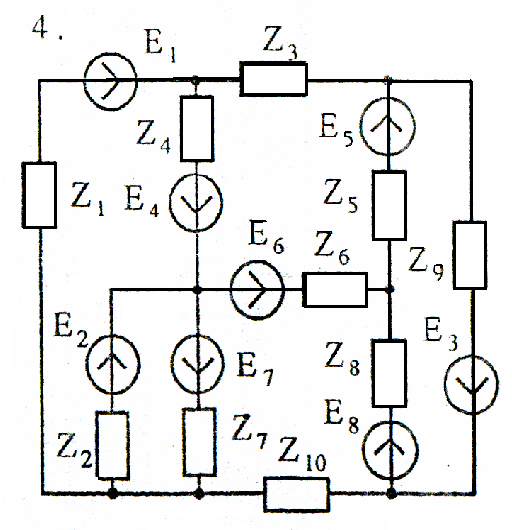
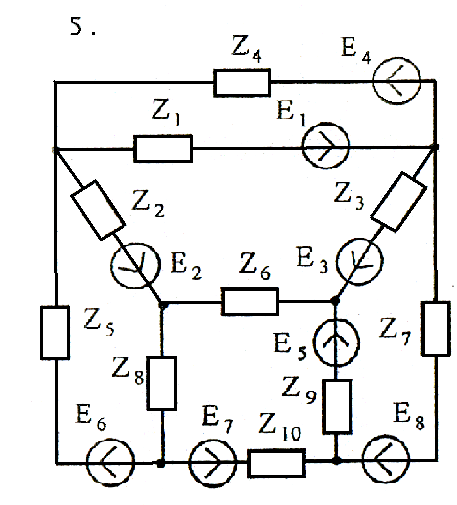
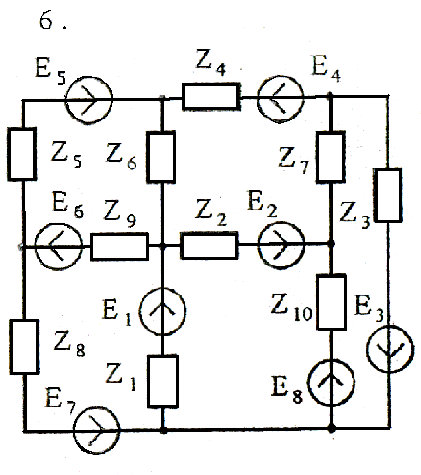
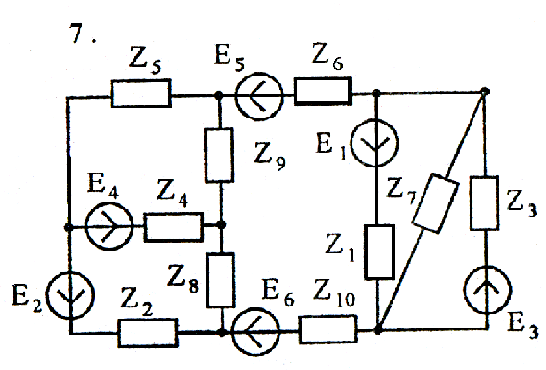
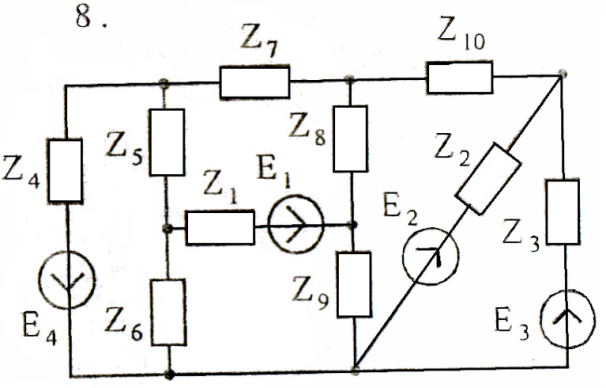
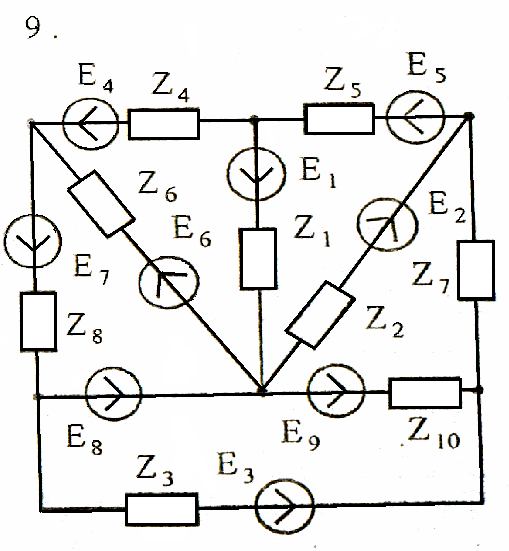
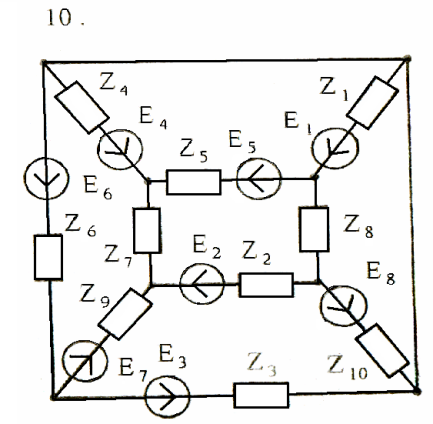
Задача 4

В цепи (рисунок 23) три источника питания, ЭДС которых равны E₁,E₂,E₃; их внутренние сопротивления соответственно равны R₀₁ = 0,1 Ом; R₀₂ = 0,2 Ом; R₀₃ = 0, 3 Ом. Отдельные ветви цепи могут быть разомкнуты при помощи рубильников P₁, P₂, P₃, P₄, P₅, P₆. Сопротивления в пассивных ветвях R₁ = 1,5 Ом; R₂ = 21 Ом; R₃ = 2,5 Ом; R₄ = 2 Ом; R₅ = R₆ = R₇ = R₈ = 3 Ом. Определить по методу непосредственного применения законов Кирхгофа токи во всех ветвях и режимы работы источников энергии. Составить баланс мощностей. Данные взять из табл. 4 (номер варианта соответствует порядковому номеру студента в журнале, номеру 11 соответствует 1 вариант).

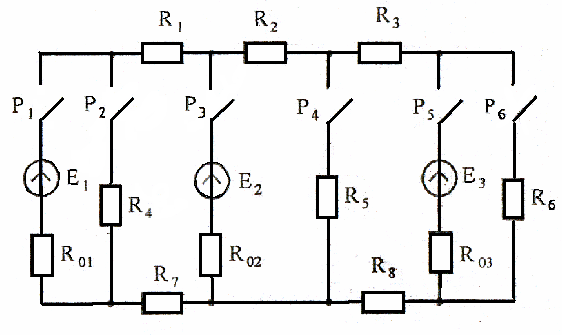
Рисунок 23

Таблица 4

Вариант	Данные к задаче 4
E1,В	E2,В	E3,В	Разомкнуты рубильники
				P4,P5,P6
				P2,P5,P6
				P2,P4,P5
				P1,P4,P6
				P2,P3,P6
				P4,P5,P6
				P2,P4,P5
				P2,P3,P6
				P1,P4,P6
				P2,P5,P6

Задание №2. Цепи однофазного синусоидального тока

Задачей расчёта электрической цепи является определение токов в её ветвях, напряжений на участках цепи или потенциалов узлов. При этом задаются: конфигурация цепи, параметры ее элементов и ЭДС, источников. Для расчёта токов в сложных электрических цепях применяются методы уравнений Кирхгофа, контурных токов, узловых потенциалов, эквивалентного генератора.

Теоретические положения

Метод уравнений Кирхгофа

Расчёт линейных электрических цепей методом законов Кирхгофа сводится к решению систем алгебраических уравнений относительно неизвестных токов. Так как число неизвестных токов в заданной схеме равно числу ветвей n этой схемы, то система алгебраических уравнений должна иметь n-й порядок.

Пусть k – число узлов схемы. Из принципа непрерывности токов следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k-1).Недостающие уравнения, число которых [n-(k-1)], составляются по второму закону Кирхгофа для независимых контуров, не содержа­щих источников тока. Контуры являются независимыми, если в каждый из них вхо­дит ветвь, не входящая во все остальные.

Рассмотрим на примере расчёт токов в схеме (рисунок 24), которая содержит 6 ветвей, 4 узла и 3 независимых контура. Выберем произвольно направление токов в ветвях и направление обхода независимых контуров. Первые три уравнения (4 - 1 = 3) запишем по первому закону Кирхгофа, а оставшиеся три (6 - 3 = 3) – по второму закону Кирхгофа:

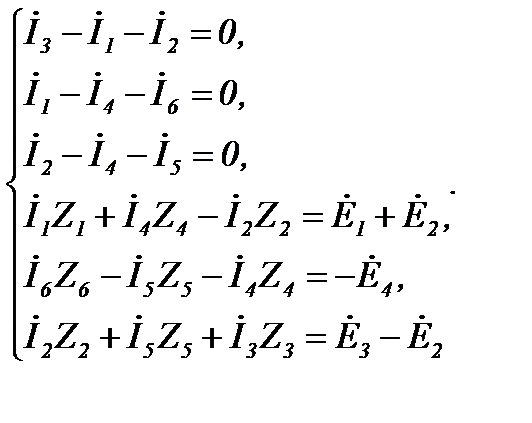
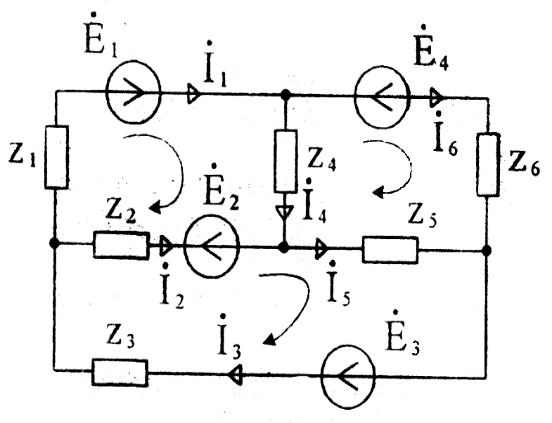
Рисунок 24

Решение полученной системы уравнений дает искомые токи. Если цепь содержит m ветвей с источниками тока, то число неизвестных токов уменьшается до (n-m). По первому закону Кирхгофа число уравнений остается без изменений (k-1), а по второму закону Кирхгофа она соответственно уменьшается на число ветвей с источниками тока [n-(k-1)-m].

Так, для схемы Рисунок 25, содержащей 6 ветвей и один источник тока, необходимо составить три уравнения по первому закону Кирхгофа и два – по второму.

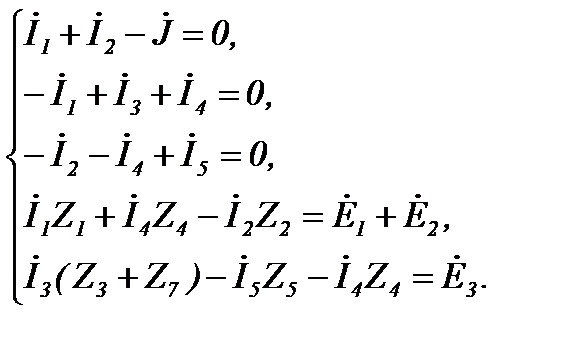
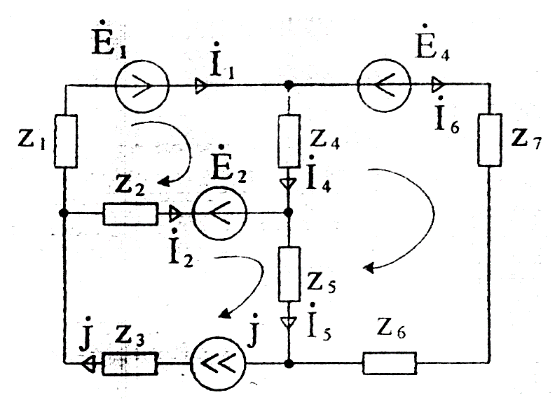
Рисунок 25

Если в результате расчётов какой-либо ток получился отрицательным, это значит, что его действительное направление противоположно выбранному.

К недостатку рассмотренного метода следует отнести высокий порядок системы уравнений для расчёта сложных электрических цепей.

Метод контурных токов

Расчёт разветвлённой цепи может быть сведён к решению всего [n-(k-1)] уравнений, составленных по второму закону Кирхгофа. Для этого цепь рассматривается как совокупность независимых соприкасающихся контуров и производится условная замена неизвестных токов в ветвях на токи, протекающие по замкнутым контурам. В уравнения, составленные по второму закону Кирхгофа, вводятся токи в независимых контурах – контурные токи.

Действительные токи в ветвях, принадлежащих только одному контуру, равны соответствующим контурным токам (но могут отличаться от них по направлению). Токи в общих для двух или нескольких контуров ветвях определяются как алгебраическая сумма соответствующих контурных токов. Первый закон Кирхгофа при этом будет выполняться автоматически. Направление контурных токов выбирается произвольно, а обход контуров усло­вимся проводить в направлении контурных токов.

Для цепи с источниками ЭДС система уравнений, составленных для независимых контуров по второму закону Кирхгофа, содержит уравнения типа

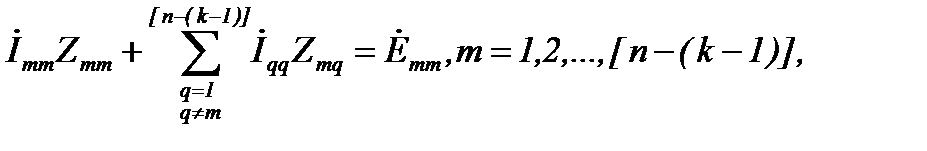
где 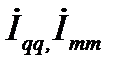– контурные токи;

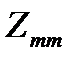– сумма сопротивлений ветвей, образующих независимый m-й контур (контурное сопротивление), ;

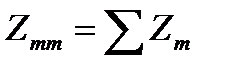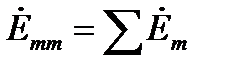– сумма ЭДС этого контура;

Z_mq – сопротивление ветви, общей для m-го и q-контура (сопротивление связи).

Если в общих (смежных) ветвях направления контурных токов совпадают, то сопротивление связи берётся положительным, если токи направлены встречно, то – отрицательным. Контурные сопротивления всегда принимаются положительными.

При записи правой части уравнений ЭДС, направления которых совпадают с принятым направлением контурного тока (обхода), принимаются положительными, а при направленных противоположно – отрицательными.

Запишем систему уравнений по методу контурных токов для схемы Рисунок 26:

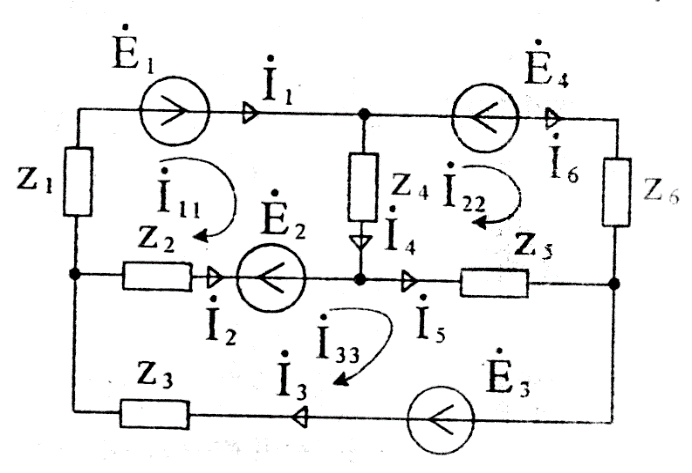
Рисунок 26

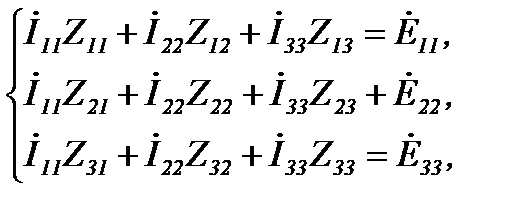
где

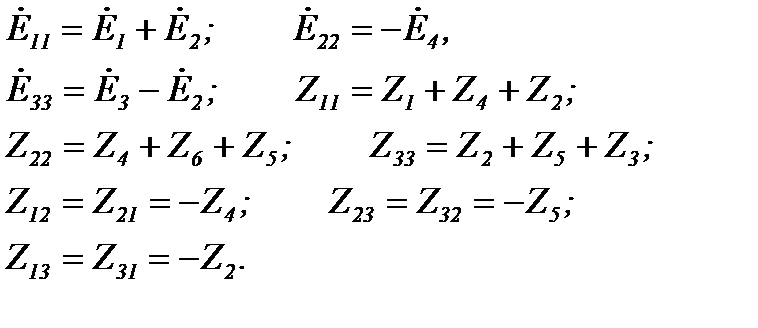
После решения системы уравнений относительно контурных токов находим токи в ветвях:

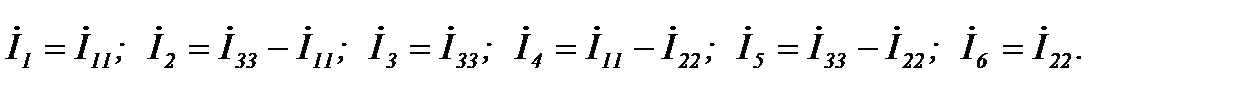При наличии ветви с источником тока выбирается дополнительный контур, включающий эту цепь. Уравнение для дополнительного контура не составляется, т.к. контурный ток равен току источника. Падения напряжения на сопротивлениях связи с другими от источника тока (контурного тока) учитываются. Так, для цепи (рисунок 27) система уравнений имеет вид

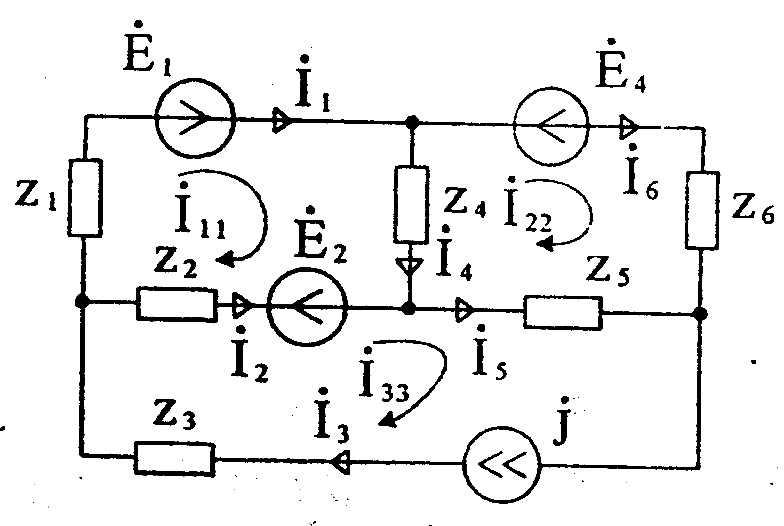
Рисунок 27

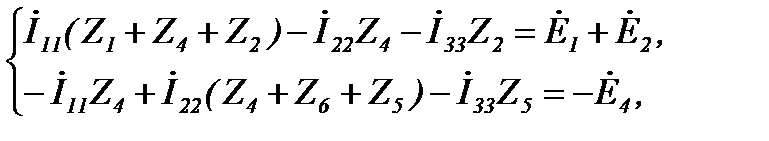
где.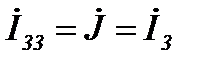

Метод узловых потенциалов

Если в разветвлённой электрической цепи число узловбез единицы меньше, чем число независимых контуров (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.

Уравнения с узловыми потенциалами вытекают из первого закона Кирхгофа. После нахождения неизвестных потенциалов определяют токи в ветвях по закону Ома.

Уравнения, входящие в систему, являются однотипными и для m-го узла имеют следующий вид:

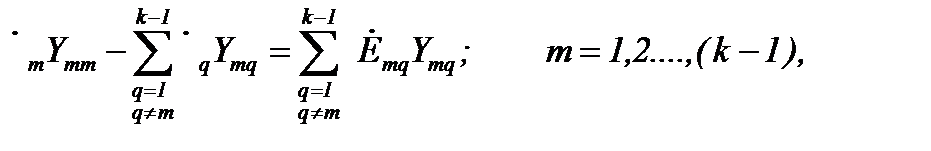
где 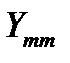– сумма проводимостей всех ветвей, сходящихся в m-ом узле, ;

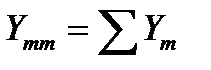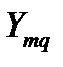– проводимость ветви, соединяющей узел m c узлом q. Если между какими-либо узлами нет ветви, то соответствующая проводимость равна нулю;

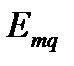– ЭДС источников, расположенных в ветви между узлами m или q.

При этом ЭДС, направленные к узлу m (относительно которого составляется уравнение), берутся положительными, а направленные от этого узла – отрица­тельными.

Составим систему уравнений для схемы Рисунок 28, полагая :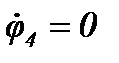

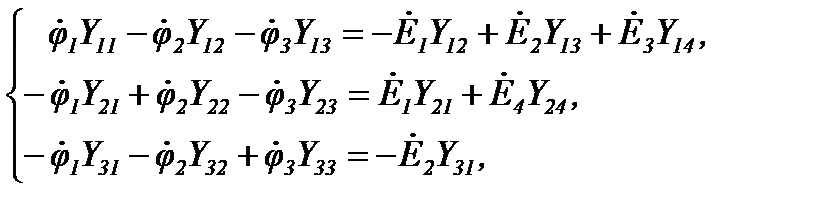
где

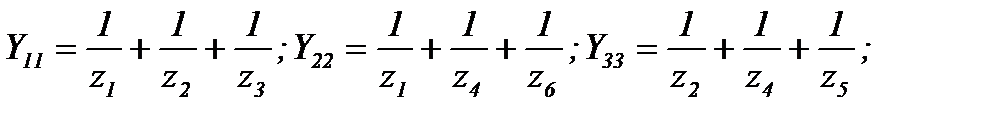
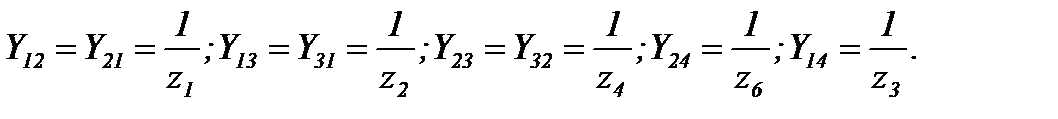
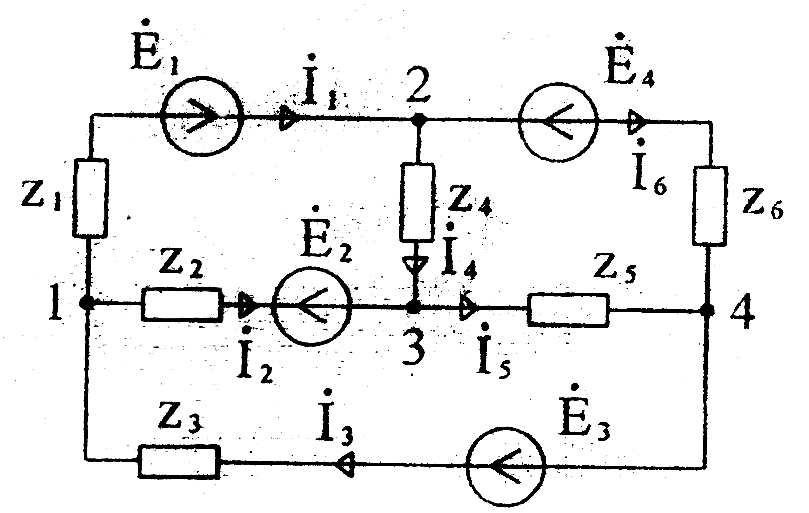
Рисунок 28

После определения потенциалов находим токи по закону Ома:

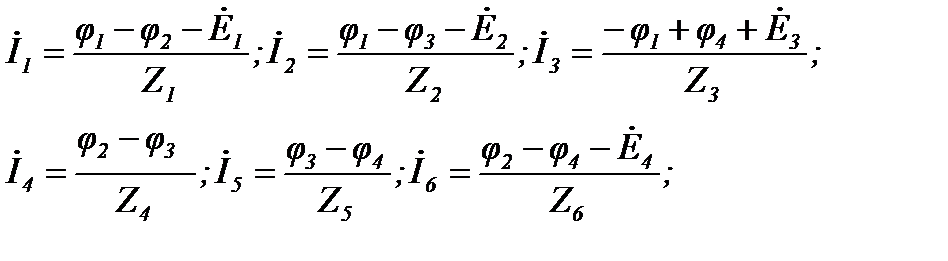
Если ветвь содержит источник тока, то её проводимость равна нулю, т.к. внутреннее сопротивление источника тока равно бесконечности. Если к m-му узлу подтекает ток от источника тока, то он должен быть включен в правую часть уравнения со знаком «плюс», если утекает, то со знаком «минус». Так, для цепи (рисунок 29) система уравнений имеет вид при :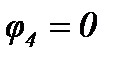

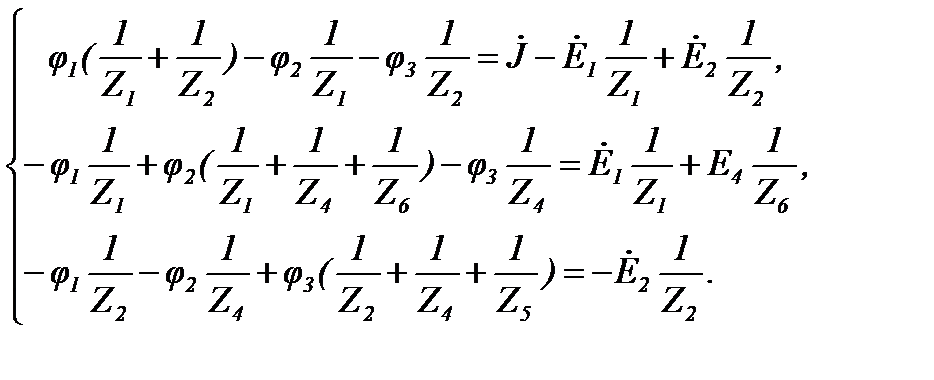
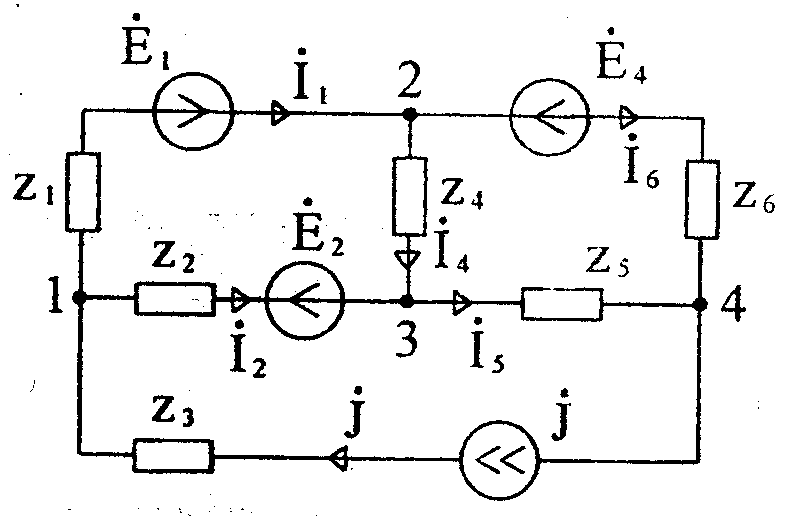
Рисунок 29

Баланс мощностей

В любой электрической цепи по закону сохранения энергии количество выра­батываемой за единицу времени энергии источников должно равняться мощности потребителей:

Р_ист=Р_потр, Q_ист=Q_потр.

Любое нарушение этих соотношений указывает на неточность проведённых вычислений.

Активную и реактивную мощности источников можно найти как действительную и мнимую части полной комплексной мощности источников:

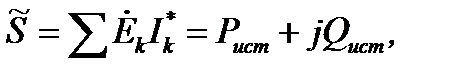
где 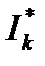– сопряженный комплекс тока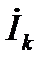

Если направление тока совпадает с направлением источника ЭДС, то произве­дение 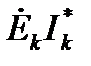входит в левую часть равенства со знаком «плюс», в противном случае – со знаком «минус».

Если электрическая цепь содержит источник тока j, то

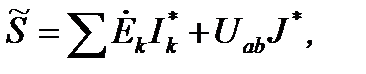
где 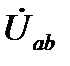– напряжение на зажимах источника тока.

Активная мощность потребителей:

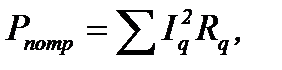
где I_q – действующее значение тока q-й ветви, содержащей активное сопротивление R_q.

Реактивная мощность потребителей:

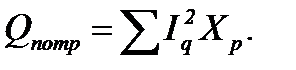
Для индуктивности произведение I²X_L входит в сумму со знаком «плюс», для емкости I²X_c – со знаком «минус».