Не является алгеброй, так как не принадлежит А (определитель этой матрицы равен 0)
Контрольная работа для заочников по дискретной математике.
Множества.
1. Найти А È В, А Ç В, А \ В, А D В, булеан А Ç В.
| № варианта | Множество А | Множество В |
| {1,2,3,5,{2},{2,3}} | {1,3,4,{2},{1,3}} |
Решение:
А È В={1,2,3,4,5,{2},{1,3},{2,3}}
А Ç В={1,3,{2}}
А \ В={2,5,{2,3}}
А D В={2,4,5,{1,3},{2,3}}
булеан А Ç В: {{1},{3},{1,3},{1,2},{2,3},{1,2,3},{2}}
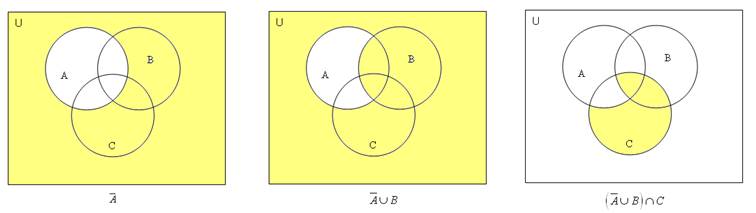
2. Изобразить множество D с помощью кругов Эйлера.
| № | Множество D |
| (`А È B) Ç C |
Решение:
3. Известно, что из 100 учеников спортом увлекаются 35 учеников, программированием 30, математикой 40, спортом и программированием 12, спортом и математикой 10, программированием и математикой 8 , спортом, математикой и программированием 5 учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
| Вариант | Количество учеников n | Спортом a | программированием b | математикой c | Спортом + программированием d | Спортом и математикой e | программированием + Математикой f | Спортом + математикой + программированием g |
Решение:
Решим задачу с помощью кругов Эйлера:
Пусть А – множество увлекающихся спортом, В – программированием, С – математикой.
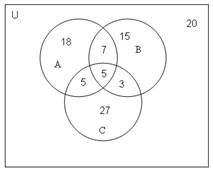
Ход рассуждений:
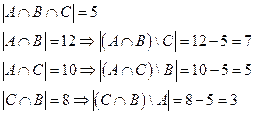
Тогда число учеников, увлекающихся только спортом: 35-7-5-5=18; только программированием: 30-7-5-3=15; только математикой: 40-5-5-3=27. Тогда число не увлекающихся ничем: 100-35-15-3-27=20.
4. Проверить следующие утверждения.
| № варианта | Утверждение 1 | Утверждение 2 |
| А Í В Û А È В = В Û А Ç В = А | 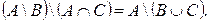 |
Решение:
Утверждение 1 верно. Докажем это с помощью кругов Эйлера:
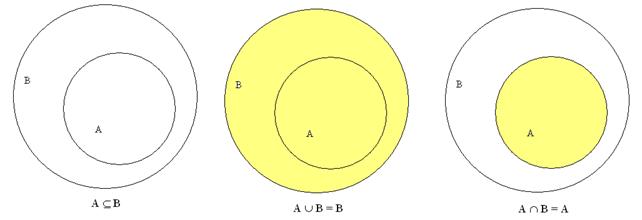
Утверждение 2:
Бинарные отношения.
1. Выписать элементы множества А ´ В.
| № варианта | А | В |
| {a,{b,c}} | {1,2,3,4} |
Решение:
А ´ В={(a,1),(a,2),(a,3),(a,4),({b,c},1),({b,c},2),({b,c},3),({b,c},4)}
2. Проверить следующие равенства.
| № варианта | Равенства |
(АÇ В)  (СÇD) = (A (СÇD) = (A  C) Ç (B C) Ç (B 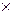 D) D) |
Решение:
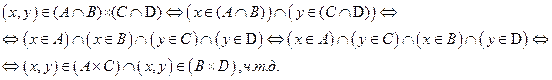
3. А={a,b,c}, B={1,2,3,4}, PÍ AxB, Q Í B2. Изобразить Р и Q графически. Записать матрицы этих отношений. Найти ( Ро Q) -1. Проверьте с помощью матрицы является ли отношение Q рефлексивным, симметричным, антисимметричным, транзитивным.
| Вариант | Р | Q |
| {(a,2),(a,4),(a,3),(c,1),(c,3)} | {(1,1),(1,4),(2,3),(3,3),(4,1),(4,3),(4,4)} |
Решение:
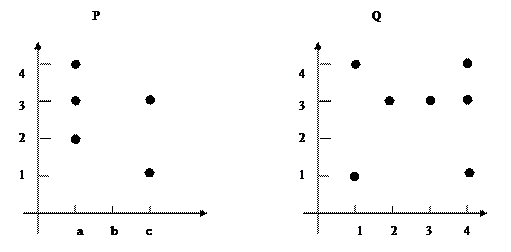
Матрица P:
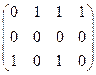
Матрица Q:
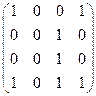
P◦Q={(a,3),(a,1),(a,4), (c,4),(c,3),(c,1)}
(P◦Q)–1={(3,a),(1,a),(4,a), (4,c),(3,c),(1,c)}
Отношение рефлексивно, если на главной диагонали матрицы нет нулей, следовательно, данное отношение Q нерефлексивно.
Отношение симметрично, если исходная и транспонированная матрицы совпадают.
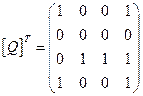
Матрицы не совпадают, значит, отношение не является симметричным.
Отношение называется антисимметричным, если из того, что  и
и  , следует
, следует 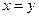 (т.е. в матрице нет ни одного симметричного элемента). В данном примере это не так (
(т.е. в матрице нет ни одного симметричного элемента). В данном примере это не так ( 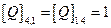 ), следовательно, отношение не является антисимметричным.
), следовательно, отношение не является антисимметричным.
Отношение транзитивно, если при перемножении матрицы самой на себя не появляется ненулевых элементов на месте нулевых:
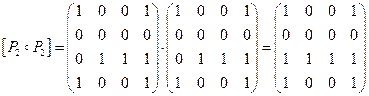
Данное отношение не является транзитивным, поскольку 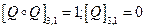 .
.
4. Найти область определения и область значений для отношения Р. Проверить, является ли отношение Р рефлексивным, симметричным, антисимметричным, транзитивным:
| № | Отношения |
| P = {(x,y)| x,y Î R и x2<y} |
Область определения R; область значений 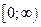 .
.
Отношение не является рефлексивным, т.к. к примеру 22>2.
Отношение не является симметричным, т.к. к примеру 12<2 и 22>1.
Отношение является антисимметричным, т.к. нет симметричных пар.
Отношение является транзитивным: 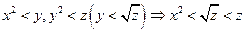 .
.
5. Рассмотрим следующие восемь отношений между людьми, а именно: «быть отцом», «быть матерью», «быть сыном» «быть дочерью», «быть братом», «быть сестрой», «быть мужем», «быть женой». Выразить через них с помощью операций над отношениями следующие отношения:
| Вариант | Отношения |
| «быть двоюродной сестрой» |
Решение:
В семье есть 2 детей (либо 2 брата, либо брат и сестра, либо 2 сестры). Хотя бы у одного из этих детей есть дочь, а второго дочь или сын. Тогда дочь первого и будет двоюродной сестрой.
6.Проверить, являются ли следующие отображения а) инъекцией; б) сюръекцией; с) биекцией.
| № | Отображение |
| F: N ® N, F(n) = n + 1 |
Отображение является инъективным, так как разным n соответствуют разные n+1. Отображение не является сюръекцией, так как для n=1 нет прообраза. Так как отображение не является сюръективным, значит, не является биекцией.
7.Пусть
F: R ® R, F(x) = x2;
G: R ® R, G(x) =sin x;
H: R ® R, H(x) =sin x2;
K: R ® R, K(x) =sin2 x.
Найти следующие произведения:
| № | Произведение |
| G2K2 |
Не ясно условие
8.Показать, что каждое из следующих отображений обратимо и найти обратное отображение.
| Вариант | Отображение |
| F: [-p/2, p/2] ® R, F(x) = tg x |
На данном интервале отображение является взаимооднозначным, тогда оно обратимо и
F-1(x) = arctg x
9.Показать, что следующие отношения являются отношениями эквивалентности.
| № | Отношение |
| r Ç s, где r и s - отношения эквивалентности на множестве А. |
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Так как оба отношения рефлексивны, то рефлексивно и их пересечение. Аналогично для симметричности и транзитивности.
Комбинаторика.
| Вариант | Задачи |
| 1. В железнодорожном вагоне десять мест расположены по ходу поезда и десять мест - против хода поезда. Сколькими способами можно посадить в вагон восемь пассажиров, если двое отказываются сидеть лицом по ходу поезда, а трое - лицом против хода поезда? 2. Сколько диагоналей можно провести в выпуклом n-угольнике? 3. У Сережи р белых и q черных шаров, р > q. Сколькими способами он может выложить все эти шары в ряд так, чтобы никакие два черных шара не лежали рядом? 4. Необходимо отправить шесть срочных писем. Сколькими способами это можно сделать, если для передачи писем можно послать пятькурьеров и каждое письмо можно дать любому из курьеров? |
1. На десять мест по ходу поезда нужно обязательно рассадить 3 пассажира ( 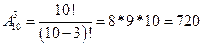 способов), на 10 мест против хода – 2 пассажира (
способов), на 10 мест против хода – 2 пассажира ( 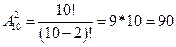 способов), остается 8-3-2=3 пассажира, которым все равно где сидеть (
способов), остается 8-3-2=3 пассажира, которым все равно где сидеть ( 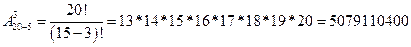 способов). Итак, всего 5079110400*720*90=329126353920000 способов.
способов). Итак, всего 5079110400*720*90=329126353920000 способов.
2. Из каждой вершины (их n) нельзя провести диагональ к двум соседним вершинам и к самой себе, поэтому (n-3). Кроме того, одна диагональ принадлежит двум вершинам. Поэтому делим на 2, тогда получим: n*(n-3)/2.
3. По формуле числа сочетаний без повторений: 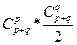
4. 6 курьеров из 5 можно выбрать по формуле сочетаний с повторениями 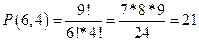 способом. Письма можно выбрать 6!= 720 способами. Тогда всего 720*21= 15120 способов.
способом. Письма можно выбрать 6!= 720 способами. Тогда всего 720*21= 15120 способов.
Алгебраические структуры
I. Является ли алгеброй следующий набор 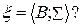
| № варианта | Набор |
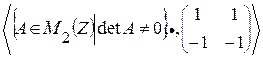 . . |
Не является алгеброй, так как не принадлежит А (определитель этой матрицы равен 0).
Графы
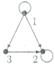
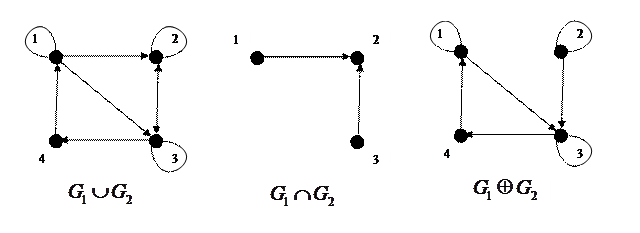
1. Даны графы 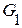 и
и 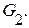 Найдите
Найдите 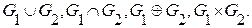 Для графа
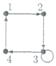
Для графа  найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
20 , 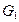 :
: 
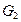 :
: 
Матрица смежности 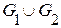 :
:
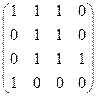
Матрица инцидентности 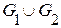 :
:
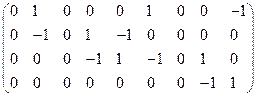
Матрица сильных компонент:
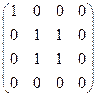
Матрица маршрутов длины 2:
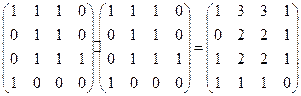
Маршруты длины 2, исходящие из первой вершины:
1-1-1; 1-1-2; 1-2-2; 1-1-3; 1-3-3; 1-2-3; 1-3-4.
2. Найдите радиус и диаметр, минимальное множество покрывающих цепей графа  . Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным? Найдите матрицы фундаментальных циклов, фундаментальных разрезов. Найти хроматическое число графа.
. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным? Найдите матрицы фундаментальных циклов, фундаментальных разрезов. Найти хроматическое число графа.
20 . 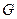 :
: 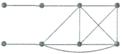
Эксцентриситеты вершин (верхний ряд слева направо, нижний справа налево):
Max(1,2,3,3,3,3,4)=4
Max(1,1,2,2,2,2,3)=3
Max(2,1,1,1,1,1,2)=2
Max(3,2,1,1,1,2,3)=3
Max(3,2,1,1,1,1,2)=3
Max(3,2,1,1,1,1,2)=3
Max(1,2,2,1,1,1,1)=2
Max(4,3,2,3,2,2,1)=4
Тогда диаметр (наибольший из эксцентриситетов) равен 4. Радиус (наименьший из них) равен 2.
Граф не является эйлеровым, так степень первой вершины равна 1.
Граф является планарным:
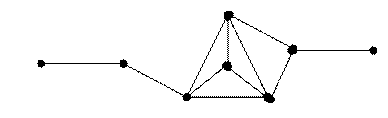
Граф незамкнутый. Поэтому нет системы фундаментальных циклов, полностью его покрывающих.
Хроматическое число равно 4:
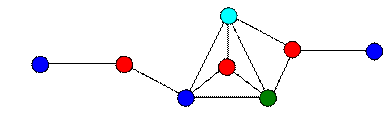
3. Для графа G , заданного матрицей весов, построить минимальный по весу остов G' и найти его вес ω(G').
20)
Булевы функции.
1.Составьте таблицы истинности формул.
| № варианта | Формула |
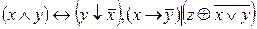 |
| Х | У | 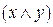 | 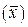 | 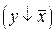 | 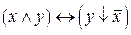 |
| Х | У | Z | 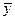 | 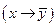 | 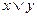 | 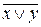 | 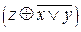 | 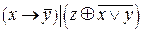 |
2. Проверьте двумя способами, будут ли эквивалентны следующие формулы
а) составлением таблиц истинности;
б) приведением формул кСДНФ или СКНФ с помощью эквивалентных преобразований.
| № варианта | Формулы |
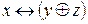 и и 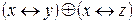 |
А)
| Х | У | Z | 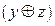 | 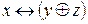 | 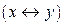 | 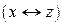 | 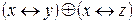 |
Формулы не эквивалентны.
Б)
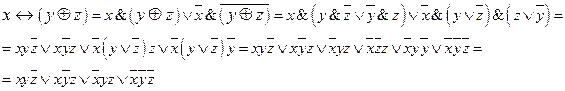
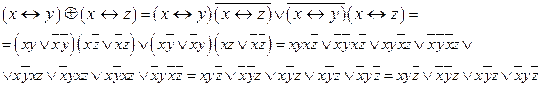
СДНФ не совпадают.
3.Выполните задание, соответствующее вашему варианту.
Запишите для следующих формул двойственные.
Запишите равносильности, двойственные следующим:
| № варианта | Формулы |
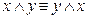 ; ; |
Составим таблицу истинности:
| Х | У | 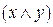 | 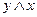 | 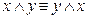 | Двойственная |
Двойственная функция: 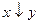 .
.
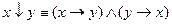
4. Для функций, заданных своим вектором значений, постройте полином Жегалкина.
| (0011 0011 0101 1100). |
Таблица истинности:
| х | y | z | t | f |
Общий вид полинома Жегалкина:
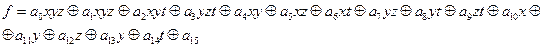
Найдем коэффициенты:
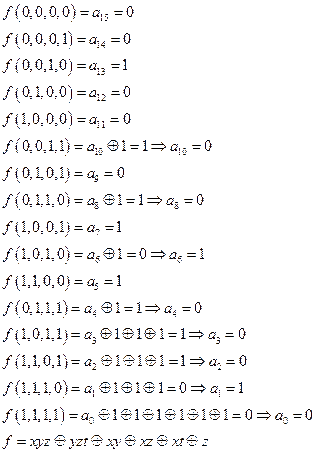
5. Является ли полной система функций? Образует ли она базис?
| № варианта | Система |
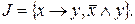 |
Проверим по критерию Поста. Составим таблицы истинности данных функций.
| Х | У | 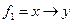 | 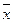 | 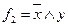 |
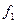 принадлежит классу Р1 (
принадлежит классу Р1 ( 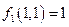 ) и не принадлежит классу Р0 (
) и не принадлежит классу Р0 ( 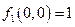 ).
).
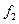 принадлежит не классу Р1 (
принадлежит не классу Р1 ( 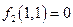 ) и принадлежит классу Р0 (
) и принадлежит классу Р0 ( 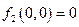 ).
).
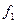 и
и 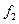 не принадлежат классу М (
не принадлежат классу М ( 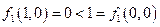 и
и 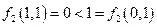 ).
).
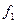 и
и 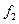 не принадлежат классу S (
не принадлежат классу S ( 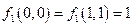 и
и 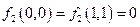 ).
).
Линейность:
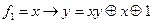 не является линейной, тогда
не является линейной, тогда 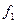 не принадлежит L.
не принадлежит L.
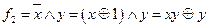 не является линейной, тогда
не является линейной, тогда 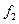 не принадлежит L.
не принадлежит L.
Составим таблицу Поста:
| Классы функций | 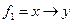 | 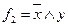 |
| Р0 | – | + |
| Р1 | + | – |
| М | – | – |
| S | – | – |
| L | – | – |
В каждом столбце таблицы есть знак «–», следовательно, система целиком не лежит ни в одном из классов Поста, тогда данная система полна. Базисом она является, так как она является полной, при этом при удалении 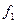 или
или 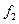 система не будет полной.
система не будет полной.
