Класичні нерівності між середніми та їх доведення

Середнім для дійсних чисел 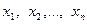назвемо довільне дійсне число 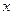, яке не перевищує найбільшого із заданих чисел та не менше від найменшого. Тобто

.

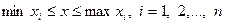Якщо 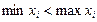, то середніх є безліч. Із середніми величинами часто зустрічаються у статистиці, фізиці, техніці. Їх використання зумовлене необхідністю оцінювати результати багаторазових вимірювань одних і тих самих величин, а також багаторазового визначення дослідним шляхом одних і тих самих параметрів.

Можна обґрунтувати, що середнім для дробів 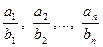з додатними знаменниками є число 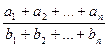, для додатних чисел 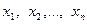середніми є величини , , , .

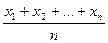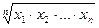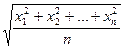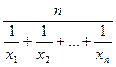З множини всіх середніх, як правило, виділяють ті, які отримують в результаті певних цілеспрямованих обчислень. У математиці такими вважають середнє арифметичне, середнє геометричне, середнє квадратичне та середнє гармонічне. Всі вони пов’язані між собою певними залежностями, які ми називаємо класичними нерівностями між середніми.

Розглянемо детальніше класичні нерівності між середніми. Як уже було зауважено, для 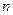додатних чисел 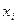такими є:

середнє арифметичне ;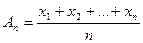

середнє геометричне ;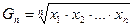

середнє квадратичне ;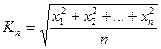

середнє гармонічне .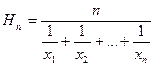

Ці середні величини знаходяться у співвідношеннях

.

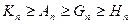Є ряд способів їх доведення. В даному посібнику ми розглянемо три із них, причому два доведення будуть наведені дещо пізніше у відповідності до методів доведень. Зараз зупинимося на першому. Спочатку доведемо наступне твердження.

Лема. Якщо добуток 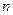додатних чисел 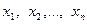дорівнює 1, то їхня сума не менша від 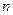, тобто 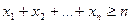. Причому рівність має місце лише тоді, коли .

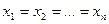Доведення виконаємо, користуючись методом математичної індукції. При 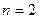нам потрібно показати, що для двох додатних чисел 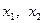таких, що 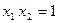, виконується нерівність 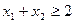. Справді,

.

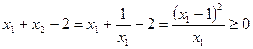Очевидно, що знак рівності виконується при 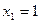. Але тоді і 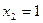, тобто .

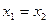Нехай для 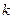додатних чисел таких, що 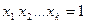, виконується нерівність 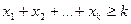. Причому рівність має місце лише тоді, коли 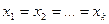. Покажемо, що 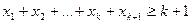, якщо тільки 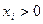і .

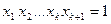Можливі два випадки:

1) всі числа 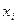рівні між собою, тобто 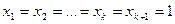. Тоді ;

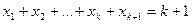2) не всі числа 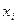рівні. У цьому випадку серед них знайдуться числа як більші, так і менші 1. Для зручності міркувань вважатимемо 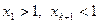. Поклавши 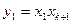, отримуємо, що 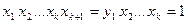. Тому, згідно з припущенням, для чисел 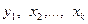виконується нерівність 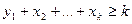. Звідси

.

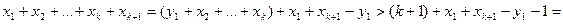
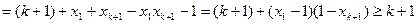Згідно з принципом математичної індукції лема доведена.

Дану лему застосуємо при доведенні нерівностей 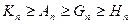. Їх можна виконувати різними способами. Ми використаємо метод математичної індукції. При цьому базою (початковим етапом доведення) для її використання служитимуть нерівності 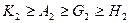, тобто нерівності

.

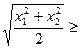
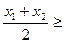
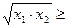
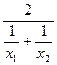Розглянемо їх доведення.

Серед різних можливих способів доведення нерівності 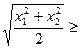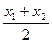виберемо, наприклад, методом від супротивного. Нехай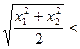 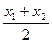. Після піднесення до квадрату невід’ємних виразів в обох частинах нерівності отримуєм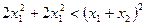о або 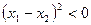, що невірно. Зроблене нами припущення невірне, отже, нерівність доведена.

Нерівність Коші 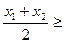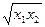ми доводили раніше.

Нерівність між середнім геометричним та середнім гармонічним можна довести, підставивши у нерівність Коші 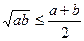значення 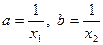. Дістаємо 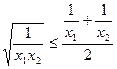, звідки знаходимо, що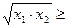 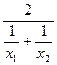. Зауважимо, що середнє геометричне двох чисел 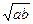іноді називають середнім пропорційним, оскільки у цьому випадку це число є розв’язком рівняння .

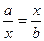Доведення нерівносте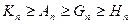й при 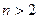розіб’ємо на доведення співвідношень 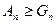, 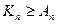та .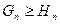

Розпочнемо з доведення нерівності 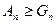або .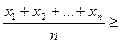

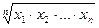Візьмемо 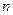додатних чисел 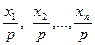, де 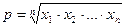. Очевидно, що їх добуток дорівнює 1. В силу доведеної нами леми, 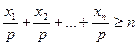, причому рівність має місце лише тоді, коли 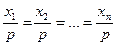. Звідси 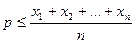, тобто

.

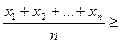
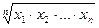Рівність має місце лише при умові, що .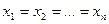

Для доведення співвідношення 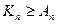або 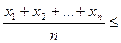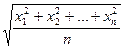припустимо, що воно вірне при 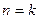, тобто, що виконується нерівність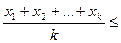 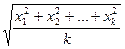, або 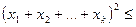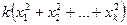. Покажемо, що з цього припущення випливає вірність нерівності

,

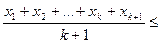
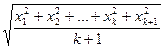або

.

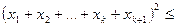
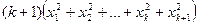Маємо

.

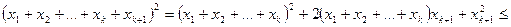
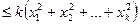
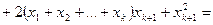
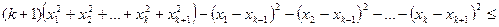
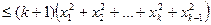Таким чином, згідно з принципом математичної індукції, нерівність 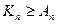доведена.

Доведення співвідношення 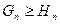або 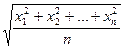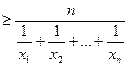випливає з нерівності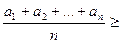 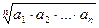з використанням замін .

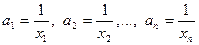Таким чином, нерівності 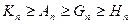доведено. Зауважимо, що знак рівності у них виконується лише у випадку, коли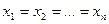

Співвідношення між середніми часто використовують при доведенні інших нерівностей. Наведемо приклади.

Задача 1.7.1. Довести, що для довільних додатних чисел 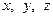виконується нерівність

.

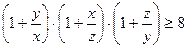Доведення. Використавши нерівність Коші, запишемо три вірні нерівності:

.

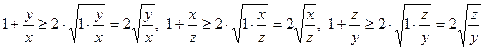Перемноживши їх, отримаємо

.

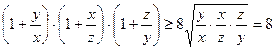Задача 1.7.2. Довести, що для довільних чисел 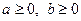виконується нерівність

.

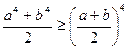Доведення. Насамперед зауважимо, що ця нерівність є частинним випадком нерівності

,

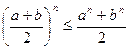яка була доведена нами раніше за допомогою методу математичної індукції. Виберемо інший спосіб доведення.

Із вірної нерівності 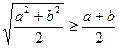, що пов’язує середні квадратичне та арифметичне, отримуємо 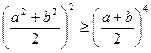. Покажемо, що 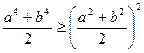, чим самим доведемо і початкову нерівність. Справді, після простих перетворень отримуємо .

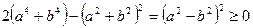Задача 1.7.3. Довести, що для довільних чисел 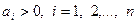виконується нерівність

.

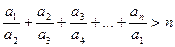Доведення. Для чисел 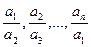використаємо нерівність між середнім арифметичним та середнім геометричним. Отримаємо нерівність

,

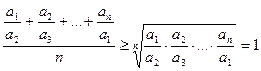звідки випливає необхідне твердження.

Задача 1.7.4. Довести, що для довільних чисел 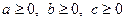виконується нерівність

.

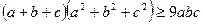Доведення. Для кожного з двох множників у лівій частині застосуємо нерівність між середнім арифметичним та середнім геометричним. Отримаємо

.

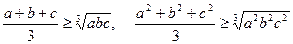Перемноживши одержані співвідношення, дістаємо нерівність, що потрібно довести.

Задача 1.7.5. Довести, що для довільних додатних чисел 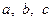виконується нерівність

.

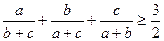Доведення.. Виконаємо наступні перетворення цієї нерівності:

,

.

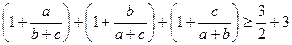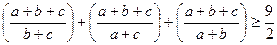Застосуємо до виразів в одержаному співвідношенні нерівність між середнім арифметичним та середнім гармонічним. Отримуємо:

,

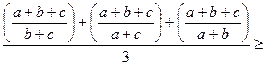
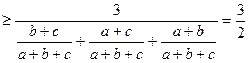звідки дістаємо шукану нерівність.

Задача 1.7.6. Довести, що при 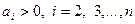виконується нерівність

.

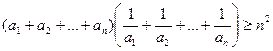Доведення.. Використаємо нерівність 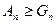для доданків першого та другого множника. Дістаємо дві нерівності

,

.

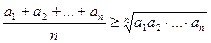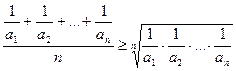Перемноживши одержані співвідношення, отримуємо потрібний результат.

Задача 1.7.7. Довести, що при 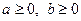виконується нерівність

.

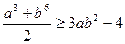Доведення. Перепишемо нерівність у виді 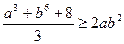і для перетворення її лівої частини для чисел 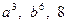використаємо нерівність 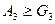. Дістаємо нерівність 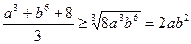, що і потрібно було довести.

Задача 1.7.8. Довести, що при 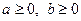виконується нерівність

.

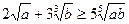Розв’язання. Перепишемо нерівність у виді 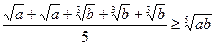і для перетворення її лівої частини використаємо нерівність 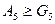. Дістаємо співвідношення 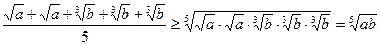, яке доводить задану нерівність.

Задача 1.7.9. Для додатних чисел 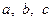довести нерівність

.

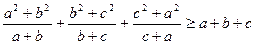Доведення. Для перетворення чисельників у кожному доданку лівої частини використаємо нерівність між середнім квадратичним та середнім арифметичним. Отримуємо:

.

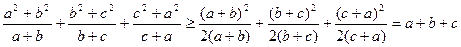Задача 1.7.10. При додатних 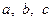знайти найменше значення виразу

.

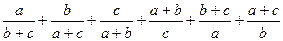Розв’язання. Насамперед покажемо, що для перших трьох доданків виконується нерівність

.

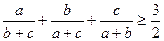Для цього виконаємо наступні перетворення:

, .

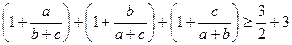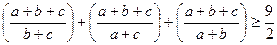Тепер, застосувавши нерівність між середнім арифметичним та середнім гармонічним, отримуємо:

.

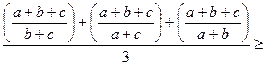
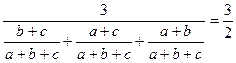Групу з інших трьох доданків перетворимо так:

.

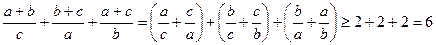Таким чином, найменше значення виразу дорівнює 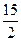. Досягається воно при .

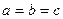Задача 1.7.11. При додатних 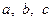довести нерівність

.

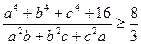Доведення. Користуючись двічі нерівністю Коші, дістаємо

.

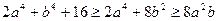Аналогічно отримуємо ще дві нерівності

, .

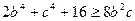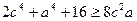Додаючи одержані три нерівності, отримуємо

,

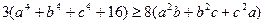звідки випливає нерівність, яку ми доводимо.