Теоремы об изменении момента количества движения точки и системы

Теорема об изменении момента количества движения точки

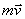Из двух основных динамических харак­теристик, величина является векторной. Иногда при изучении движения точки вместо изменения самого вектора 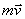оказывается необходимым рассматривать изменение его момента. Мо­мент вектора 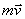относительно данного центра О или оси z обозна­чается 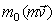или 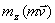и называется соответственно моментом количества движения или кинетическим моментом точки отно­сительно этого центра (оси). Вычисляется момент вектора 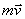так же, как и момент силы. При этом вектор 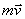считается приложенным к движущейся точке. По модулю 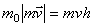, где h - длина перпендикуляра, опущенного из центра О на направление вектора 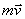(рис.11).

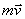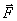Теорема моментов отно­сительно центра. Найдем для ма­териальной точки, движущейся под дей­ствием силы F (рис.26), зависимость между моментами векторов и отно­сительно какой-нибудь неподвижного центра О. В конце было показано, что .

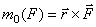Аналогично .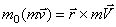

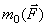При этом вектор направлен перпендикулярно плоскости, проходящей через центр О и вектор 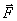, а вектор 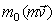- перпендикулярно плоскости, проходящей через центр О и вектор .

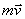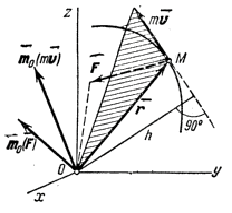
Рис.26

Дифференцируя выражение 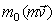по времени, получаем:

.

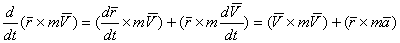Но 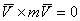, как векторное произведение двух параллельных векторов, a 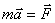. Следовательно,

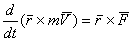
или .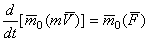

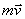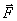В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Аналогичная теорема имеетместо для моментов вектора силы относительно какой-нибудь оси z, в чем можно убедиться, проектируя обе части равенства 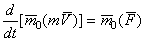на эту ось. Ма­тематическое выражение теоремы моментов относительно оси дается формулой .

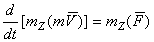Главный момент количеств движения системы

Главным моментом количеств движения (или кинетическом моментом) системы относительно данного центра О называется величина 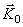, равная геометрической сумме моментов количеств движения всех точек системы относи­тельно этого центра.

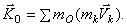
Аналогично определяются моменты количеств движения системы относительно координатных осей:

, , .

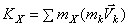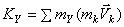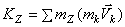При этом 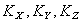представляют собою одновременно проекции вектора 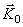на координатные оси.

Подобно тому, как количество движения системы является характеристикой ее поступательного движения, главный момент количеств движения системы является характеристи­кой вращательного движения системы.

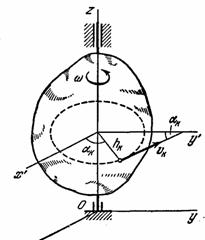
Рис.45

Чтобы уяснить механический смысл величины 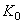и иметь необхо­димые формулы для решения задач, вычислим кинетический момент тела, вращающегося вокруг неподвижнойоси (рис.45).Приэтом, как обычно, определение вектора 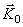сводится к определению его проекций .

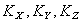Найдем сначала наиболее важ­ную для приложений формулу, оп­ределяющую величину К_z, т.е. кине­тический момент вращающегося тела относительно оси вращения.

Для любой точки тела, отстоя­щей от оси вращения на расстоя­нии 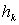, скорость 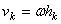. Сле­довательно, для этой точки 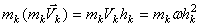. Тогда для всего тела, вынося общий множитель за скобку, получим

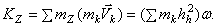
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Окончательно находим

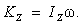
Таким образом, кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то, очевидно, будет

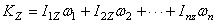
Легко видеть аналогию между формулам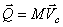и и 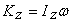: количество движения равно произведению массы (величина, характеризующая инертность тела при поступательном движении) на скорость; кинети­ческий момент равен произведению момента инерции (величина, характеризующая инертность тела при вращательном движении) на угловую скорость.