Уравнения равнопеременного движения

ФИЗИЧЕСКИЕ ОСНОВЫ

МЕХАНИКИ

Учебное пособие для студентов

института путей сообщения

Челябинск

УДК 531 (07)

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. Учебное пособие по физике для студентов института путей сообщения.

Учебное пособие представляет собой курс лекций по физике. Пособие написано в соответствии с программой для инженерно-технических специальностей высших учебных заведений. Однако, в отличие от Общего курса физики в данном учебном пособии дополнительно рассмотрены вопросы применения физических законов к процессам на железнодорожном транспорте. Таких как создание силы тяги локомотива, динамики поезда, динамики вагона, собственных и вынужденных колебаний вагона, колебаний тягового двигателя на рессорах подвески и т.д.

В конце каждой главы приведены контрольные задачи. Все формулы и решения задач приведены в Международной системе единиц СИ.

Авторы: А. В. Шушарин, ст. преподаватель кафедры ЕНД,

М.А. Круглова, доцент кафедры ЕНД.

Рецензенты: А.Е. Гришкевич, профессор кафедры

Общей и теоретической физики ЮУрГУ,

канд. физ.мат. наук;

В. Л. Федяев, доцент, зам. директора ЧИПС,

канд. техн. наук;

Печатается по решению научно-методического Совета

Челябинского института путей сообщения

Филиал Уральского государственного университета путей сообщения

Челябинский институт путей сообщения, 2010.

ВВЕДЕНИЕ

«Физика – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи, и законы её движения» (БСЭ).

Материя – это та реальность, из которой создан окружающий мир, которую можно обнаружить посредством ощущений. Материя существует в двух видах: как вещество и как силовые поля. Всякое изменение материи является движением. Простейшая форма движения материи – механическое движение – это процесс изменения взаимного расположения тел или их частей в пространстве с течением времени. Раздел физики, занимающийся изучением закономерностей механического движения, называется механикой.

Развитие механики, как науки, было вызвано потребностями техники и строительства. Древнейшие постройки Египта свидетельствуют о знании закона равновесия тел. Началом следует считать III в. до н.э., когда древнегреческий ученый Архимед сформулировал закон рычага и законы равновесия плавающих тел. Развитие механики было продолжено в 16 – 17 веках трудами Коперника, Кеплера, Гюйгенса, и особенно Галилея, впервые применившего экспериментальный метод исследования. Окончательно основные законы классической механики были экспериментально установлены и сформулированы И. Ньютоном в его многотомном труде «Математические начала натуральной философии» (1687 г.). В этом сочинении был воплощен идеал научной теории – отыскание количественных закономерностей в явлениях природы. Дальнейшее развитие механики шло по созданию аналитических методов решения задач, по созданию новых направлений механики. Развитие не прекращается и в наше время. В 20 веке были созданы новые области механики: релятивистская механика и квантовая механика, со своими законами и методами решения задач (рис.1).

В классической механике изучаются законы движения макроскопических тел со скоростью меньше скорости света (V<3∙10⁸ м/с) и на расстоянии до 10²² м (но может быть и далее). Макроскопические тела это обычные тела, содержащие громадное количество молекул.

Закономерности механического движения микрообъектов (атомы, элементарные частицы) изучает квантовая механика.Критерием применения законов микромира является универсальная константа – постоянная Планка ћ =1,054·10^-34 Дж∙с. Если момент импульса частицы сопоставим с постоянной Планка, mVr ≈ ħ, то проявляются волновые свойства частиц, исчезает понятие траектории. Неизвестны законы движения на расстоянии менее, чем 10^{-20 м. Может, здесь уже следует учитывать дискретность пространства и времени?}

Закономерности 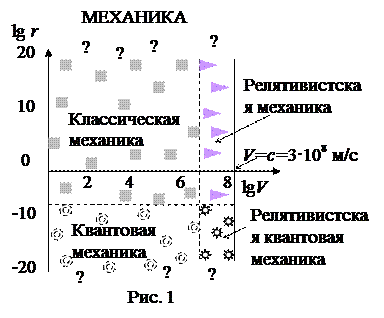движения тел со скоростями, близкими к скорости света, изучает релятивистская механика или специальная теория относительности. Её основой является постулат Эйнштейна о существования предельной скорости движения материи, равной скорости света в вакууме. Движение с большей скоростью теорией запрещено.

Квантовая механика и релятивистская механика являются более общими научными теориями, чем классическая механика. Они установили границы применения классической механики. Законы квантовой и релятивистской механики переходят в законы классической механики в предельном случае движения тел большой массы в большой области пространства с малыми скоростями. Но классическая механика не утратила своего значения с созданием более общих теорий, поскольку поправки новых теорий в задачах техники ничтожно малы.

Классическая механика подразделяется на три части. Кинематика (от греческого слова kinema – движение) – раздел механики, в котором изучаются законы движения тел без учета их массы и действующих на них сил. Динамика (от греческого dynamis – сила) изучает движения тел в связи с теми причинами, которые обусловливают это движение. Статика (от греческого statike – равновесие) изучает условия равновесия тел.

Механическое движение тел происходит в пространстве и времени. Эти понятия прочно связаны с нашим житейским опытом и кажутся нам очевидными и незыблемыми. Со времен Ньютона в классической механике постулируется, что пространство и время имеют абсолютный характер, т.е. существуют независимо друг от друга, от находящихся в них объектов и протекающих процессов. Но в ходе развития физики и философии эти понятия претерпели существенные изменения. В релятивистской механике пространство и время связаны между собой.

Пространство в классической механике однородно, изотропно и эвклидово (его геометрия описывается геометрией Эвклида). Однородность пространства означает, что любая его точка равноправна. То есть начало отсчета координатной системы можно перенести в любую точку пространства; этот перенос никак не влияет на процессы, происходящие с телом. Изотропность пространства означает равноправие всех направлений, то есть, если все оси системы координат повернуть, то это не изменит протекающие процессы. Время в классической механике – абсолютная реальность, не зависящая от тел, оно однородно и во всей Вселенной течет равномерно и одинаково. Однородность времени означает равноправность всех его моментов, т.е. время протекает непрерывно и одинаково от прошедшего к будущему, и любой из его моментов может быть выбран за начало отсчета любого процесса при одинаковых условиях.

Физика является фундаментальной наукой. Она является базой всех технических дисциплин, её законы используются в самых разных разделах науки и техники. Знание физики повышает кругозор образованного человека, он более критично относится к сверхновым теориям, к ложным наукам. Для специалиста путей сообщения особенно важна механика, так как движение транспортных средств на Земле вполне подчиняется законам классической механики. Прочное знание механики повышает компетентность специалиста при решении технических проблем.

Системы единиц измерения физических величин

Измерить какую-либо физическую величину - это значит сравнить ее с другой однородной физической величиной, принятой за единицу измерения. Единицы измерения сводятся в систему, охватывающую единицы всех физических величин и позволяющую оперировать с ними. Для построения системы произвольно выбирают единицы для нескольких не зависящих друг от друга величин. Эти величины называются основными. Остальные величины и их единицы выводятся из законов, связывающих их с основными единицами. Они называются производными.

Т.к. выбор основных единиц произволен, то может быть построен целый ряд систем единиц: СГС, СГСЭ, МКС, МКГСС и др. Во всем мире и в нашей стране (болеет 80 лет) в качестве предпочтительной принята Международная система единицСИ – единая система для всех разделов физики. В этой системе основными единицами измерения являются:

длины L – 1 метр (м), равный 1.650.763,73 длин волн излучения оранжевого цвета изотопа криптона 86 в вакууме;

массы m – 1 килограмм (кг), равный массе международного прототипа килограмма;

времени t – 1 секунда (с), равная 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133;

температуры T – 1 кельвин (К), равный 1/273,15 термодинамической температуры затвердевания дистиллированной воды при давлении 101 325 Па;

количества вещества v – 1 моль, содержащий столько атомов, сколько содержится в 0,012 кг нуклида углерода С₁₂;

силы тока J – 1 ампер (А), который, проходя по двум параллельным | прямым проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенных на расстоянии 1 м в вакууме, вызывает силу 2∙10^-7 Н на каждый метр длины;

силы света I – 1 канделла (Кд), равная силе света в заданном на правлении источника, испускающего монохроматическое излучение частотой 540 · 10¹² Гц, энергетическая сила света которого в этом направлении составляет 1/ 683 Вт/ср.

Дополнительные единицы: рад (радиан) – единица плоского угла, ср (стерадиан) – единица телесного угла.

1. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Основные понятия кинематики

Существует два основных вида движения тел: поступательное и вращательное. При поступательном движении любая прямая, связанная с телом, остается параллельной самой себе, поэтому изучение движения тела сводится к изучению движения любой точки тела. Тело можно принять за материальную точку, масса которой равна массе тела. Материальной точкой называется макроскопическое тело, размеры и форму которого можно не учитывать в данной задаче. Например, движение поезда между станциями можно рассматривать как движение материальной точки.

Положение материальной точки в пространстве можно определить только относительно других тел. Тело отсчета, связанная с ним система координат и способ отсчета времени образуют систему отсчета. Положение материальной точки в пространстве определяется радиус-вектором 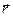. Радиус-вектор – это вектор, соединяющий начало системы координат с положением материальной точки в пространстве (рис. 1.1). Зависимость радиус-вектора от времени называется основным кинематическим уравнением движения 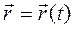.Проекции радиус-вектора на координатные оси определяют координаты тела x, y, z

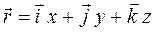, (1.1)

где 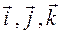единичные орты координат. Уравнения зависимости координат от времени определяют положение материальной точки в пространстве .

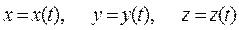Если из этих уравнений исключить время t , мы получим уравнение траектории – линии, вдоль которой двигалось тело. Траектория – понятие относительное, форма траектория зависит от выбора системы отсчета. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Для рельсового транспорта траектория определяется расположением рельсов.

Параметрами поступательного движения материальной точки по траектории являются вектор перемещения и путь. Перемещение – это вектор, соединяющий начальную и конечную точки траектории (рис.1.1). Путь – это длина траектории или расстояние, проходимое телом от начала до конца движения. На рис 1.1 это длина пунктирной линии. Путь – величина скалярная и положительная. По величине путь и перемещение равны при прямолинейном движении в одном направлении или на бесконечно малом участке траектории.

Скорость

Быстрота изменения вектора перемещения во времени характеризуется скоростью. Мгновенная скорость 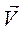это вектор, равный отношению бесконечно малого перемещения 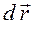ко времени перемещения:

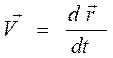. (1.2)

То есть скорость равна первой производной от вектора перемещения по времени. Вектор мгновенной скорости, как и вектор перемещения 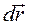, направлен по касательной к траектории в сторону движения.

Продифференцировав по времени уравнение (1.1) получим уравнение для вектора скорости через проекции на оси координат

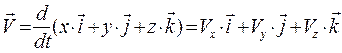, (1.3)

где 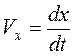, , 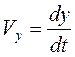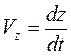. Модуль вектора скорости определяется по теореме Пифагора .

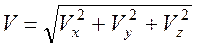При бесконечно малом перемещении длина пути dS приближается к величине элементарного перемещения 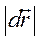. Поэтому величина мгновенной скорости может быть определена также как первая производная от пути по времени

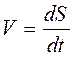. (1.4)

Неравномерное движение тела с переменной по величине скоростью характеризуют средней скоростью

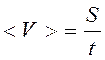.(1.5)

По определению средняя скорость неравномерного движения равна отношению всего пути ко всему времени движения.

Ускорение

При движении тела скорость может быть не постоянна. Быстрота изменения скорости характеризуется ускорением. Ускорение,по определению, равно отношению бесконечно малого изменения вектора скорости 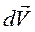ко времени dt этого изменения:

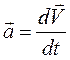. (1.6)

То есть ускорение – это вектор­, равный первой производной от вектора скорости по времени. Через проекции вектора ускорения на декартовы оси координат 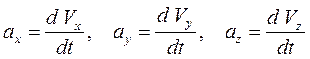, вектор полного ускорения равен 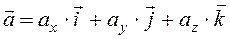. Величина полного ускорения по теореме Пифагора равна .

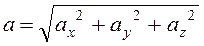Кроме этого, принято представлять полное ускорение как векторную сумму составляющих ускорения на касательное и нормальное направление к траектории 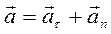. Их называют соответственно касательным (тангенциальным) и нормальным (центростремительным) ускорениями. Величина полного ускорения равна .

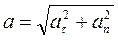Представим вектор скорости, который направлен по касательной, как произведения модуля скорости на единичный вектор касательной 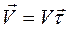. Определим ускорение как первую производную от этого произведения по времени

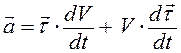. (1.7)

Первый член формулы характеризует изменение скорости по величине и определяет касательное ускорение 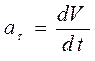. Второй член формулы определяет скорость поворота единичного вектора и характеризует изменение скорости по направлению. Это нормальное ускорение, которое направлено к центру кривизны траектории.

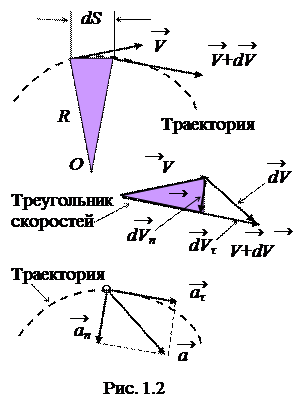Выведем формулу нормального ускорения. Разложим вектор полного изменения скорости на составляющие: на нормаль 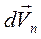и на касательную к траектории 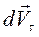(рис. 1.2). При бесконечно малом перемещении дугу dS можно принять за отрезок. Заштрихованные равнобедренные треугольник расстояний и треугольник скоростей подобны, Условие подобия 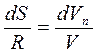. Подставим сюда путь 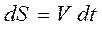, получим

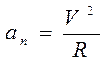. (1.8)

Уравнения равнопеременного движения

Движение точки называется равнопеременным, если вектор ускорения постоянен.

Так как, исходя из определения ускорения, элементарное приращение скорости равно 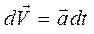, то полное изменение вектора скорости за конечное время равно сумме элементарных приращений скорости, т.е. равно интегралу от ускорения по времени 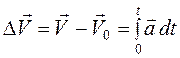. Откуда скорость в момент времени t может быть определена по уравнению

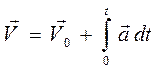. (1.9)

Элементарное изменение радиус-вектора точки, по определению скорости, равно 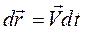. Полное изменение вектора перемещения за конечное время будет равно сумме элементарных приращений, то есть будет равно интегралу от вектора скоростипо времени 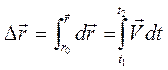. Откуда, радиус – вектор равен

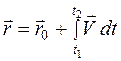(1.10)

Применим эти уравнения для вывода скорости и радиус-вектора точки при равнопеременном движении. Равнопеременное движение – это движение с постоянным по величине и по направлению ускорением. Например, полет тела в поле тяжести Земли с ускорением свободного падения g = 9,81 м/с².

Получим уравнение для скорости. Для этого проинтегрируем уравнение (1.9) при постоянном векторе ускорения, 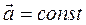, в результате получим

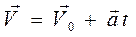. (1.11)

Подставив формулу скорости (1.11) под знак интеграла для вектора перемещения, получим основное кинематическое уравнение равнопеременного движения

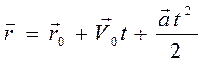. (1.12)

При решении конкретных задач векторные уравнения (1.11) и (1.12) проецируют на выбранные оси координат и получают систему уже алгебраических уравнений для решения задачи.