Расчет элементов направляющего устройства подвески

Элементы направляющего устройства подвески рассчитывают при следующих режимах нагружения:

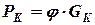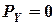1. Сила тяги при , где 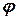-- коэффициент сцепления колеса с опорной поверхностью в продольном направлении: 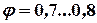; 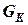-- вес автомобиля, приходящийся на колесо.
2. Тормозная сила 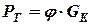при ; .
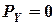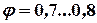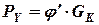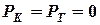3. Боковая сила при , где 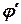-- коэффициент сцепления колеса с опорной поверхностью в поперечном направлении: .
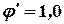4. Вертикальная сила 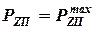при .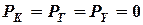

Значение 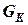соответствует условию перераспределения нагрузки на колеса автомобиля для данных режимов движения.

зависимая балансирная подвеска

Для схемы такой подвески, показанной на рис.2.4, определим нагрузки на реактивные штанги.

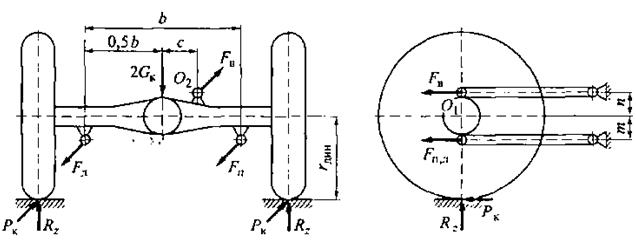
Рис. 2.4. Расчетная схема зависимой балансирной подвески

Для первого режима нагружения уравнения условия равновесия будет иметь вид:

: ;

: ;

: .

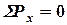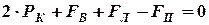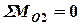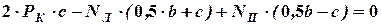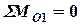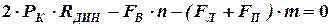После преобразований получим:

;

;

.

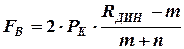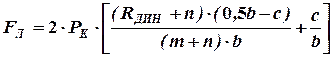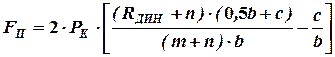Для обеспечения равномерного износа шарниров и равнопрочности штанг необходимо выполнить условие: 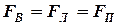. Это условие выполняется при:

;

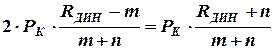или

.

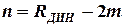зависимая подвеска с четырьмя продольными и одной поперечной штангами

Такую подвеску применяют для ведущих мостов легковых автомобилей. Продольные штанги такой подвески воспринимают тормозной момент и силы, действующие в продольном направлении. Тяга Панара служит для передачи боковых сил между мостом и несущей системой автомобиля.

Если упругий элемент опирается на продольную штангу (рис. 2.5-а), то последняя будет дополнительно воспринимать вертикальную нагрузку от части подрессоренной массы автомобиля, приходящейся на данный упругий элемент.

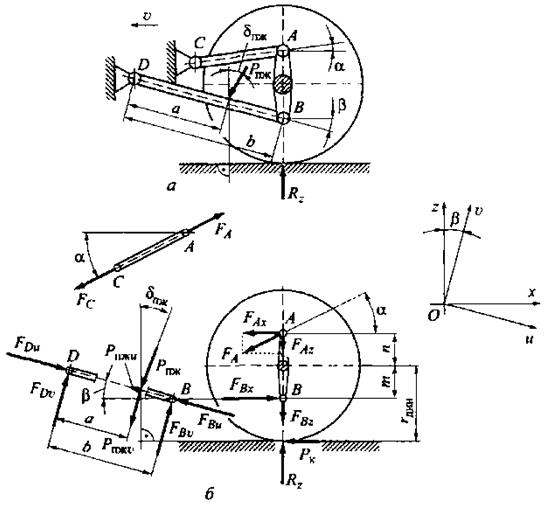
Рис. 2.5. Расчетные схемы: а – зависимой подвески с четырьмя продольными и одной поперечной штангами; б - для определения сил в шарнирах штанг направляющего устройства

Статическая вертикальная нагрузка на пружину будет:

,

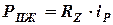где 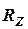-- вертикальная реакция от веса подрессоренной массы автомобиля, приходящаяся на колесо;

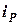-- силовое передаточное число направляющего устройства подвески.

Для первого режима нагружения силы в местах соединения продольных штанг с несущей системой автомобиля и балкой моста (рис. 2.5-б) из условия равновесия:

: ; ;

: ;

: .

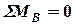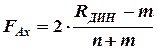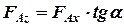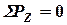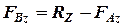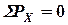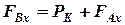Если нижняя штанга расположена под углом 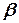в продольной плоскости, то для определения сил, действующих на шарнир D этой штанги, следует разложить полученные силы 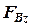и 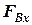на составляющие, действующие вдоль осе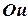й и 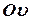, связанных с штангой:

; ;

; .

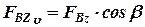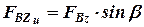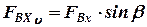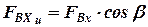Откуда: ; .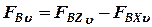

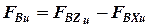Используя полученные выражения для усилий в шарнирах, из условия равновесия нагрузка на штангу от пружины будет:

: ; .

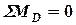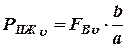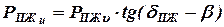Откуда:

;

.

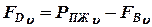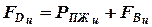Полученные значения сил позволяют выполнить расчеты прочности штанг направляющего устройства: верхней – на растяжение; нижней – на сжатие и изгиб.

Тяга Панара рассчитывается на растяжение, сжатие и продольный изгиб от силы, определяемой по третьему режиму нагружения:

,

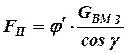где 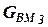-- вес автомобиля, приходящийся на задний ведущий мост;

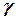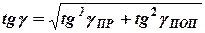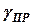-- пространственный угол наклона тяги Панара: , где и 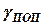-- углы наклона тяги в продольной и поперечной плоскостях соответственно.

НЕЗАВИСИМАЯ ДВУХРЫЧАЖНАЯ ПОДВЕСКА

Расчетная схема такой подвески представлена на рис 2.6.

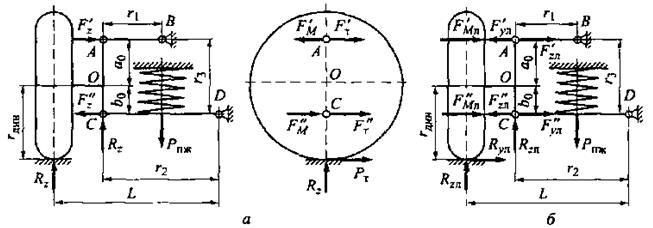
Рис. 2.6. Расчетная схема независимой двухрычажной подвески: а – для первого режима нагружения; б – для второго режима нагружения

При втором режиме нагружения сила 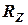на плече ( 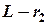) создает момент, который уравновешивается моментом 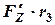на вертикальной стойке. Тогда

.

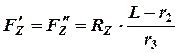Под действием тормозной силы 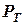и момента 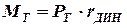в шарнирах рычагов в продольной плоскости возникают силы:

; ; ,

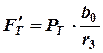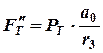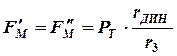а в горизонтальной плоскости – момент:

.

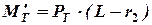В результате этого верхний рычаг испытывает изгиб от силы ( 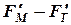) и момента 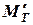, и сжатие – от силы 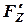. А нижний рычаг – изгиб от сил 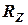, , 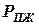( 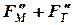) и момента 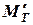, а также растяжение от силы .

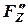При третьем режиме нагружения (рис. 2.5-б) из равенства моментов от нагрузки 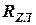на левом колесе будем иметь на стойке:

.

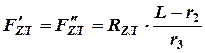Боковая сила и её момент создают на рычагах силы:

; ; .

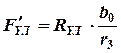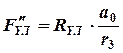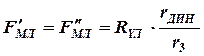Таким образом, верхний рычаг стойки при этом режиме нагружения работает на сжатие или растяжение от силы ( 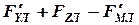), а нижний – на изгиб от сил 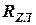и 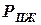, и на сжатие от силы ( ).

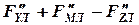НЕЗАВИСИМАЯ РЫЧАЖНО-ТЕЛЕСКОПИЧЕСКАЯ ПОДВЕСКА

Расчетные схемы такой подвески представлены на рис. 2.7.

При четвертом нагрузочном режиме колесо (1), его поворотная цапфа (2) наружная труба (3) амортизатора и его шток (4) для рассмотрения условия равновесия представляют собой единое целое по отношению к точке А крепления штока и в точке В установки нижнего рычага. На рис. 1.25-б показана освобожденная система, в которой опоры заменены соответствующими реакциями, расположенными в направлении осей 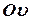и . 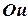Ось 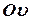совпадает с осью амортизатора и образует в поперечной плоскости угол 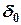, относительно вертикали (поперечный угол наклона оси поворота колеса).

Уравнение моментов относительно точки В (рис. 2.7-а) имеет вид:

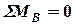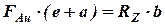: , или ,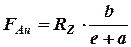

где .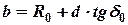

Анализ этого уравнения показывает, что чем меньше плечо обкатки ( 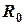) и выше расположена точка А (больше расстояние ( 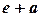)), тем меньше будет сила 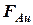, создающая изгиб штока амортизатора.

Поскольку сумма всех сил в направлении оси 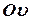равна нулю, то статическую нагрузку 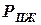на пружину можно определить из условия:

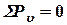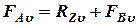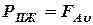: ; или ,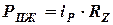

где ; .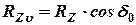

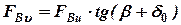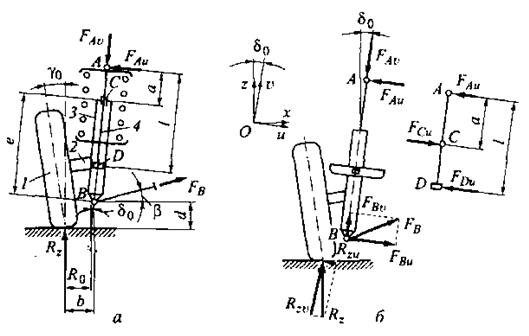
Рис. 2.7. Расчетные схемы независимой рычажно-телескопической подвески:

а – схема нагружения; б – схема определения сил в шарнирах телескопической стойки

В проекциях на ось 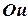имеем:

: ,

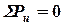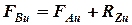где .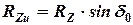

В соответствии со схемой на рис. 2.7-б, изгибающий момент на штоке амортизатора:

,

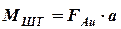сила, действующая на его направляющую втулку:

,

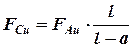а сила, действующая на поршень амортизатора:

.

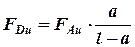Чем короче отрезок а, тем меньше силы 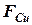и 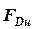, а значит, силы трения в направляющей втулке и на поршне.

Для уменьшения плеча обкатки 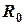на переднеприводных автомобилях опору В стараются сместить от оси амортизатора к колесу на расстояние 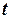(рис. 2.8-а). При этом между осью амортизатора и осью поворота колеса образуется угол 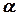, который можно выразить через известные длины отрезков:

.

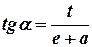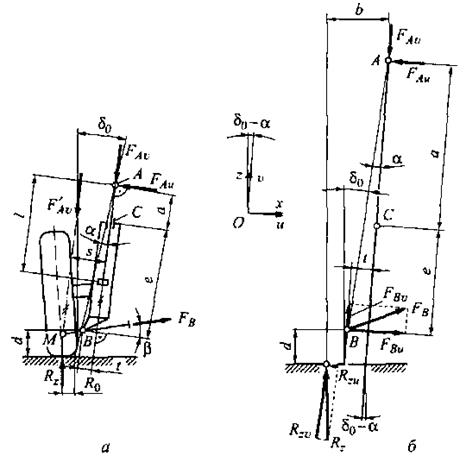
Рис. 2.8. расчетные схемы для определения смещения пружины в рычажно-телескопической подвеске

На рис. 2.8-б показано разложение сил в системе координат 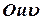. Уравнение моментов относительно точки А будет:

: .

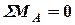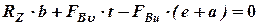При этом: ;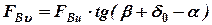

.

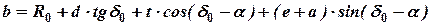Тогда с учетом последнего уравнения моментов можно определить 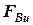и .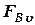

Для определения силы сжатия пружины 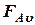и нагрузки в шарнире А ( 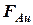) разложим нагрузку на колесо 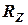на две составляющие:

;

.

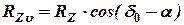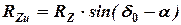Выше было сказано, что сила 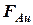должна быть как можно меньше. Условие: 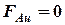(а значит 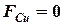и и 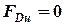) выполняется в том случае, если пружина смещена к колесу или наклонена так, что положение её оси попадает в точку М пересечения линий действия сил 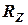и 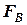(рис. 2.8-а). при выполнении этого условия, силы, действующие на пружину 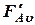и рычаг 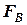, можно вычислить по формулам:

;

.

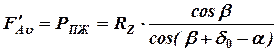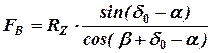Смещение пружины в сторону колеса:

.

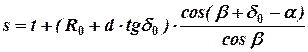Если значения 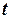и 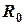малы, то и необходимое смещение пружины может быть небольшим.

С расчетом силовых факторов при других схемах направляющего устройства подвески можно познакомиться в литературе.