Арифметика, алгебра и начала анализа
ПРОГРАММА
ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПРИ ПРИЁМЕ
В ФИЛИАЛ ВУНЦ ВВС «ВВА»
(г. СЫЗРАНЬ)
ПО СПЕЦИАЛЬНОСТИ:161002 Лётная эксплуатация и применение
Авиационных комплексов.
МАТЕМАТИКА
Порядок проведения экзамена.
Поступающий в филиал ВУНЦ ВВС «ВВА» (г. Сызрань) сдает письменный экзамен по математике. Работа выполняется в течении 4-х часов. Основой подготовки к вступительным экзаменам является систематическая самостоятельная работа по всему материалу школьной программы с использованием стабильных учебников и задачников по алгебре, геометрии и основам анализа. К поступающим в филиал ВУНЦ ВВС «ВВА» (г. Сызрань) предъявляются достаточно высокие требования по математике, что должно обеспечить уровень математической подготовки, необходимой для успешного овладения курсом высшей математики.
Требования к поступающему.
На экзамене по математике поступающий должен показать четкое знание математических определений и теорем, предусмотренных программой, умение точно и сжато выражать математическую мысль в письменном изложении, использовать соответствующую символику, уверенное владение математическими знаниями и навыками, умение применять их при решении задач.
Экзаменующийся должен уметь:
1.Производить арифметические действия над числами, заданными в виде десятичных и обыкновенных дробей; с требуемой точностью округлять данные числа и результаты вычислений, производить приближенную прикидку результата; пользоваться таблицами для производства вычислений.
2.Производить тождественные преобразования многочленов, дробей, содержащих переменные, выражений, содержащих степенные, показательные, логарифмические и тригонометрические функции.
3.Строить графики линейной, квадратичной, степенной, показательной, логарифмической и тригонометрических функций.
4.Решать уравнения и неравенства первой и второй степени, уравнения и неравенства, приводящиеся к ним; решать системы уравнений и неравенств первой и второй степени и приводящиеся к ним. Сюда относятся простейшие уравнения и неравенства, содержащие степенные, показательные, логарифмические и тригонометрические функции.
5.Решать задачи на составление уравнений и систем уравнений.
6.Изображать геометрические фигуры на чертеже и производить простейшие построения на плоскости.
7.Использовать геометрические представления при решении алгебраических задач, а методы алгебры и тригонометрии - при решении геометрических задач.
8.Производить операции над векторами (сложение и вычитание векторов, умножение вектора на число) и пользоваться свойствами этих операций.
9.Пользоваться понятием производной при исследовании функций на возрастание (убывание), на экстремумы, при построении графиков функций, а также при решении геометрических задач на экстремумы.
Экзаменационный билет содержит 8 задач по алгебре, геометрии и основам анализа.
ПРОГРАММА ПО МАТЕМАТИКЕ
Арифметика, алгебра и начала анализа.
Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель, наименьшее общее кратное.
Признаки делимости на 2, 3, 5, 9, 10.
Целые числа (Z).Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.
Действительные числа (R), их представление в виде десятичных дробей.
Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.
Числовые выражения. Выражения с переменными. Формулы сокращенного умножения.
Степень с натуральным и рациональным показателем. Арифметический корень.
Логарифмы, их свойства.
Одночлен и многочлен.
Многочлен с одной переменной. Корень многочлена на примере квадратного трехчлена.
Понятие функции. Способы задания функции. Область определения. Множество значений функции.
График функции. Возрастание и убывание функции; периодичность, четность, нечетность.
Достаточное условие возрастания (убывания) функции на промежутке. Понятие экстремума функции. Необходимое условие экстремума функции (теорема Ферма). Достаточное условие экстремума. Наибольшее и наименьшее значение функции на промежутке.
Определение и основные свойства функций: линейной, квадратичной
у=ах2 +вх + с, степенной у =ахn (nÎN),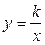 
, показательной y =ax, а>0;
логарифмической, тригонометрических функций (y = sinx; y= cosx; y= tgx),
__
арифметического корня y=Ö x .
Уравнение. Корень уравнения. Понятие о равносильных уравнениях.
Неравенства. Решения неравенства. Понятие о равносильных неравенствах.
Система уравнений и неравенств. Решения системы.
Арифметическая и геометрическая прогрессия. Формула n-го члена и суммы первых n членов геометрической прогрессии.
Синус и косинус суммы и разности двух аргументов (формулы).
Преобразование в произведение сумм sina ± sinb; cosa ± cosb.
Определение производной. Ее физический и геометрический смысл. Производные функций y = sinx; y = cosx; y = tgx; y = ax; y = xn (nÎZ).
Геометрия.
Прямая, луч, отрезок, ломаная; длина отрезка. Угол, величина угла. Вертикальные и смежные углы. Окружность, круг. Параллельные прямые.
Примеры преобразования фигур, виды симметрии. Преобразование подобия и его свойства.
Векторы. Операции над векторами.
Многоугольник, его вершины, стороны, диагонали.
Треугольник. Его медиана, биссектриса, высота. Виды треугольников. Соотношения между сторонами и углами прямоугольного треугольника.
Четырехугольник: параллелограмм, прямоугольник, ромб, квадрат, трапеция.
Окружность и круг. Центр, хорда, диаметр, радиус. Касательная к окружности. Дуга окружности. Сектор.
Центральные и вписанные углы.
Формулы площади: треугольника, прямоугольника, параллелограмма, ромба, квадрата, трапеции.
Длина окружности и длина дуги окружности. Радианная мера угла. Площадь круга и площадь сектора.
Подобие. Подобные фигуры. Отношение площадей подобных фигур.
Плоскость. Параллельные и пересекающиеся плоскости.
Параллельность прямой и плоскости.
Угол прямой с плоскостью. Перпендикуляр к плоскости.
Двугранные углы. Линейный угол двугранного угла. Перпендикулярность двух плоскостей.
Многогранники. Их вершины, грани, диагонали. Прямая и наклонная призмы; пирамиды. Правильная призма и правильная пирамида. Параллелепипеды, их виды.
Фигуры вращения: цилиндр, конус, сфера, шар. Центр, диаметр, радиус сферы и шара. Плоскость, касательная к сфере.
Формулы площади поверхности и объема призмы.
Формулы площади поверхности и объема пирамиды.
Формулы площади поверхности и объема цилиндра.
Формулы площади поверхности и объема конуса.
Формулы объема шара.
Формулы площади сферы.