Модели с бинарными фиктивными переменными

Результативная переменная у в нормальной линейной модели регрессии является непрерывной величиной, способной принимать любые значения из заданного множества. Но помимо нормальных линейных моделей регрессии существуют модели регрессии, в которых переменная у должна принимать определённый узкий круг заранее заданных значений.

Моделью бинарного выбора называется модель регрессии, в которой результативная переменная может принимать только узкий круг заранее заданных значений

В качестве примеров бинарных результативных переменных можно привести:

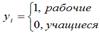
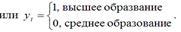
Приведенные в качестве примеров бинарные переменные являются дискретными величинами. Бинарная непрерывная величина задаётся следующим образом:

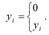
Если стоит задача построения модели регрессии, включающей результативную бинарную переменную, то прогнозные значения yi прогноз, полученные с помощью данной модели, будут выходить за пределы интервала [0;+1] и не будут поддаваться интерпретации. В этом случае задача построения модели регрессии формулируется не как предсказание конкретных значений бинарной переменной, а как предсказание непрерывной переменной, значения которой заключаются в интервале [0;+1].

Решением данной задачи будет являться кривая, удовлетворяющая следующим трём свойствам:

1) F(–∞)=0;

2) F(+∞)=1;

3) F(x1)>F(x2) при условии, чтоx1> x2.

Данным трём свойствам удовлетворяет функция распределения вероятности.

Модель парной регрессии с результативной бинарной переменной с помощью функции распределения вероятности можно представить в следующем виде:

prob(yi=1)=F(β0+β1xi), где prob(yi=1) – это вероятность того, что результативная переменная yi примет значение, равное единице.

В этом случае прогнозные значения yiпрогноз, полученные с помощью данной модели, будут лежать в пределах интервала [0;+1].

Модель бинарного выбора может быть представлена с помощью скрытой или латентной переменной следующим образом:

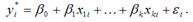
Векторная форма модели бинарного выбора с латентной переменной:

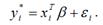
В данном случае результативная бинарная переменная yi принимает значения в зависимости от латентной переменной yi*:

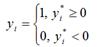
Модель бинарного выбора называется пробит-моделью или пробит-регрессией, если она удовлетворяет двум условиям:

1) остатки модели бинарного выбора εi являются случайными нормально распределёнными величинами;

2) функция распределения вероятностей является нормальной вероятностной функцией.

Пробит-регрессия может быть представлена с помощью выражения:

NP(yi)=NP(β0+β1x1i+…+βkxki),

где NP – это нормальная вероятность (normal probability).

Модель бинарного выбора называется логит-моделью или логит-регрессией (logit regression), если случайные остатки εi подчиняются логистическому закону распределения.

Логит-регрессия может быть представлена с помощью выражения:

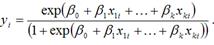
Данная модель логит-регрессии характеризуется тем, что при любых значениях факторных переменных и коэффициентов регрессии, значения результативной переменной yi будут всегда лежать в интервале [0;+1].

Обобщённый вид модели логит-регрессии:

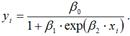
Достоинством данной модели является то, что результативная переменная yi может произвольно меняться внутри заданного числового интервала (не только от нуля до плюс единицы).

Логит-регрессия относится к классу функций, которые можно привести к линейному виду. Это осуществляется с помощью преобразования, носящего название логистического или логит преобразования, которое можно проиллюстрировать на примере преобразования обычной вероятности р:

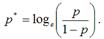
Качество построенной логит-регрессии или пробит-регрессии характеризуется с помощью псевдо коэффициента детерминации, который рассчитывается по формуле:

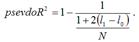
Если значение данного коэффициента близко к единице, то модель регрессии считается адекватной реальным данным.

При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую принадлежность и др.).

Фиктивной переменной наз-тся атрибутивный или качественный фактор, представленный посредством определённого цифрового кода.

Наиболее наглядным примером применения фиктивных переменных является модель регрессии, отражающая проблему разрыва в заработной плате у мужчин и женщин.

Предположим, что на основе собранных данных была построена модель регрессии, отражающая зависимость заработной платы рабочих y от их возраста х: yt=β0+β1xt.

Однако данная модель регрессии не может в полной мере охарактеризовать вариацию результативной переменной. Поэтому в модель необходимо ввести дополнительный фактор, например пол, на основании предположения о том, что у мужчин в среднем заработная плата выше, чем у женщин. В связи с тем, что переменная пола является качественной, её необходимо представить в виде фиктивной переменной следующим образом:

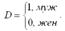
С учётом новой фиктивной переменной модель регрессии примет вид:

y=β0+β1x+β2D, где β2 – это коэффициент, который характеризует в среднем разницу в заработной плате у мужчин и женщин.

26.Моделирование тенденции временных рядов.

27. Мультиколлинеарность факторов – понятие, проявление и меры устранения.

Мультикол-ть - тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат. Эта связь затрудняет оценивание параметров регрессии в частности, при анализе эконометрической модели.

Чем выше корреляция, тем выше дисперсии и больше риск получить несостоятельные оценки. В этом случае говорят о мульти-ти. Любая регрессия страдает от мульти-ти. Задача определить, когда это влияние становится существенным.

Одним из способов обнаружения мульти-сти является вычисление коэффициентов парной корреляции между факторами. Считается, что если коэффициент корреляции превышает 0,8 (эмпирическое правило), то мульти-сть присутствует.

Меры устранения:

• дополнить модель новой информацией, по возможности, не обладающей свойствами коллинеарности(т. е. если речь идет о точках, они не должны находиться на одной прямой, если о векторах — они не должны быть параллельными друг другу, отличаясь только скалярными множителями);

• ввести некоторые ограничения на параметры модели;

• использовать вероятностные характеристики параметров (напр., опираясь на предшествующие наблюдения за соответствующими величинами).

Методы устранения мультиколлинеарности

1) Метод дополнительных регрессий

o Строятся уравнения регрессии, которые связывают каждый из регрессоров со всеми остальными

o Вычисляются коэффициенты детерминации 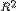для каждого уравнения регрессии

o Проверяется статистическая гипотеза 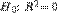с помощью F-теста

Вывод: если гипотеза не отвергается, то данный регрессор не приводит к мульти-ости.

2) Метод последовательного присоединения

o Строится регрессионная модель с учетом всех предполагаемых регрессоров. По признакам делается вывод о возможном присутствии мульти-сти

o Расчитывается матрица корреляций и выбирается регрессор, имеющий наибольшую корреляцию с выходной переменной

o К выбранному регрессору последовательно добавляются каждый из оставшихся регрессоров и вычисляются скорректированные коэффициенты детерминации для каждой из моделей. К модели присоединяется тот регрессор, который обеспечивает наибольшее значение скорректированного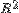

3) Метод предварительного центрирования - суть метода сводится к тому, что перед нахождением параметров математической модели проводится центрирование исходных данных: из каждого значения в ряде данных вычитается среднее по ряду: 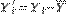. Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми.