Измерение коэффициента объемного расширения воздуха
Запороцкова И.В.
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
ЧАСТЬ 1: ГАЗЫ И ПРОЦЕССЫ В НИХ
Методическое пособие по общему физическому практикуму
Волгоград, 2010
ЛАБОРАТОРНАЯ РАБОТА 1-1
ИЗУЧЕНИЕ ЗАВИСИМОСТИ ТЕРМИЧЕСКОГО КОЭФФИЦИЕНТА ДАВЛЕНИЯ ВОЗДУХА ОТ ТЕМПЕРАТУРЫ
Цель работы
Целью работы является ознакомление с газовыми законами и методикой экспериментального определения зависимости величины термического коэффициента давления воздуха от температуры.
Теоретические пояснения
Термический коэффициент давления однородного изотропного тела определяется выражением:
β = (1/Р)( ∂Р/∂Т)V (1)
Термическим коэффициентом давления β называется относительное изменение давления тела при изменении его температуры на 1 градус при постоянном объеме.
Для газов коэффициент β часто определяется как
β = (1/Ро)( ∂Р/∂Т)V,
где Р0 - давление газа при 00 С.
Коэффициент β для моля идеального газа можно легко определить из уравнения состояния
PoV = RT. (2)
Дифференцированием Р по Т при постоянном V получим:
( ∂Р/∂Т)V =R/V . (3)
Подстановка (2) и (3) в (1) дает:
β = 1/Т . (4)
Таким образом, значение термического коэффициента давления идеального газа равно обратной температуре. В частности, при Т = То = 273К
β = βо = (1/273)К-1
Зная величину β0, можно определить давление тела при любой температуре по формуле:
Р (Т) = Ро[ 1+ βо (Т-То)], (5)
где Ро – давление при температуре То (обычно То=273 К).
Данная формула лежит в основе работы барометрических термометров (или газовых термометров), которые измеряют температуру тела по изменению давления термометрического вещества (обычно используется газ) при постоянном объеме термометра.
Установка
Установка для определения термического коэффициента давления газа состоит из стеклянной колбы (рис.1), заполненной воздухом, которая помещена в банку с водой 2. Колба соединена гибкой трубкой с V –образным водяным манометром 3. На дне колбы насыпано некоторое количество силикогеля (или другого вещества) для осушения воздуха, т.к. насыщенный водяной пар существенно исказит результаты. Воздух в колбе 1 принимает температуру воды за 3-4 мин. Температура воздуха измеряется прикрепленным к колбе термометром 4. Температура воды в банке повышается путем добавления в нее горячей (90 - 100 0С) воды, которая нагревается в стакане на электроплитке.
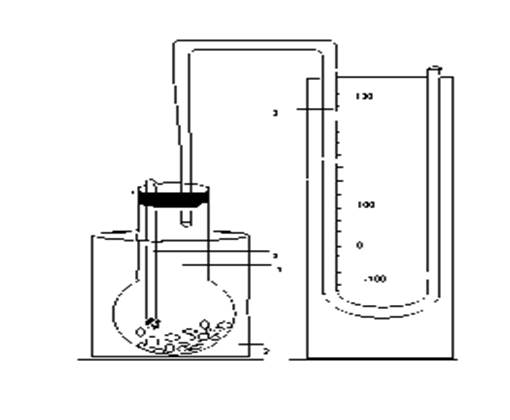
Рис.1. Установка для измерения давления воздуха в зависимости от температуры: 1 - колба с осушителем; 2 - банка с водой; 3 - водяной манометр; 4 - термометр.
Порядок выполнения работы
1. Включить плитку и поставить колбу с водой (400 – 500 мл) для нагрева до кипения.
2. Налить в банку с колбой воды до уровня ¾.
3. С помощью резиновой груши с тонким эластичным шлангом (или стеклянной трубки) залить в манометр воды до уровня –100 мл ниже уровня нулевого давления. Воду в грушу набирать из стакана (2) и сливать туда же. Если воды слишком много, ее следует слить в банку с водой.
4. Герметично соединить манометр с колбой, стараясь не нарушать равновесие. Записать показания термометра 4, т.е. температуру t, 0C, соответствующую Δh = 0.
5. Используя вспомогательный стаканчик, добавить в банку 2 примерно 70 мл горячей воды. Несколько раз осторожно переместить колбу 1 вверх-вниз для перемешивания воды и выждать 3-4 минуты, пока нагревается воздух в колбе; записать новые показания термометра. При нагревании воздуха в колбе уровень воды в правом колене манометра будет падать, и надо следить, чтобы она совсем она не была вытеснена из этого колена расширяющимся воздухом. Для этого надо с помощью резиновой груши понемногу добавлять воду в левое колено с более высоким уровнем.
Так как в работе требуется определить производную (∂Р/∂Т)V при постоянном объеме, то прежде чем записывать новое давление в колбе, соответствующее температуре t2, необходимо добавить в сообщающееся с атмосферой колено столько воды, чтобы в другом колене уровень остался первоначальным, то есть – 100 мл. После этого записать перепад уровней Δh2, численно равный избыточному по сравнению с атмосферным давлением в колбе, в мм водяного столба.
6. Повторить п.5, каждый раз доливая почти кипящую воду, столько раз, пока уровень воды в «атмосферном» колене манометра не поднимется до +130мл. Если при доливании по 70 мл уровень воды в банке будет приближаться к краю, то ее следует откачивать с помощью той же резиновой груши.
7. Поскольку истинное давление воздуха в колбе (в мм водяного столба)
Р = Ратм + h
где Ратм – атмосферное давление, определяющееся по барометру (в мм.вод.ст.), надо сделать соответствующие пересчеты и данные занести в таблицу 1.
8. Построить график Δh = f(t) и по тангенсу угла наклона отдельных участков определить ряд значений βi по формуле βi = (1/Рi)tgαi, которая следует из (1). Данные занести в таблицу 1.
Таблица 1.
| № | Δh, мм | ti, 0C | Р, мм.в.ст. | βi | Ti, К | 1/Ti | β |
| … |
9. Для проверки зависимости (4) построить графики βi = f(1/Ti ), где βi - значение коэффициента, полученные в эксперименте для соответствующих температур, и для сравнения график β= 1/Ti для тех же температур. Объяснить расхождение графиков.
Экстраполяцией найти значение βо при Т= 273 К.
10. Снять шланг с манометра и вылить воду из всех банок в раковину.
5. Контрольные вопросы
1. Дайте определение коэффициента теплового расширения α, термического коэффициента давления β, изотермической сжимаемости. Как связаны эти величины между собой в случае идеального газа?
2. Чему равен термический коэффициент давления смеси двух идеальных газов, количество молей которых ν1 и ν2, а термические коэффициенты β1 и β2?
3. Давление воздуха внутри плотно закупоренной бутылки при температуре 280 К было равно 105 Па. На сколько градусов нужно нагревать бутылку, чтобы из нее вылетела пробка, если известно, что из холодной бутылки без нагревания пробку можно вынуть силой 49 Н? Сечение пробки 4 см2. Тепловым расширением бутылки и пробки пренебречь.
4. Найти максимально возможную температуру одного моля идеального газа в процессе, описываемом уравнением Р = Р0 e-βV.
5. Вычислить коэффициент β для газа Ван-дер-Ваальса и сравнить с коэффициентом β для идеального газа.
ЛАБОРАТОРНАЯ РАБОТА 1-2
ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ОБЪЕМНОГО РАСШИРЕНИЯ ВОЗДУХА
Цель работы
Целью работы является ознакомление с газовыми законами и с методикой экспериментального определения величины коэффициента объемного расширения воздуха.
Теоретические пояснения
Коэффициентом объемного расширения газа α называют относительное изменение объема газа при увеличении его температуры на 1 градус при Р = const
α = (1/V)( ∂Р/∂Т)р (1)
Его значение легко вывести из уравнения состояния идеального газа
PV = (m/µ) RT (2)
где ν = m/µ – количество молей газа.
Дифференцируя (2) по Т при постоянном Р, получим
Р ( ∂Р/∂Т)р = ν R. (3)
Тогда из (1), (2) и (3) следует
α = 1/Т (4)
Обычно используется термический коэффициент в виде:
α = (1/V0)( ∂Р/∂Т)р , (5)
где V0 - объем тела при Т0 = 273 К.
Интегрированием (5) можно получить зависимость V(Т)
V = Vо[1+α (Т-Тo)] (6)
Формула (6) выражает закон теплового расширения тел (закон Гей-Люссака). Это явление используется в жидкостных термометрах (ртутных, спиртовых и др.) для измерения температуры тел.
Прибор для проверки закона Гей-Люссака и определения коэффициента объемного расширения воздуха изображен на рисунке 1.
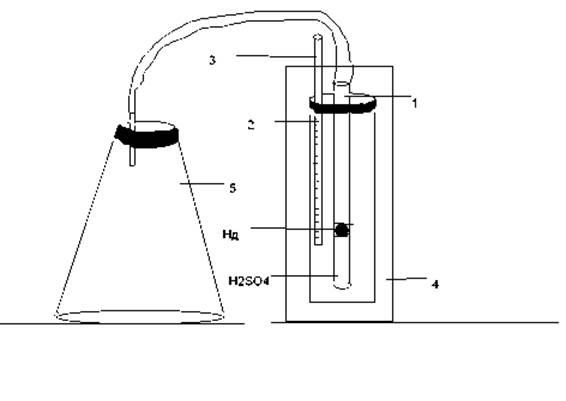
Рис. 1. Установка для определения коэффициента объемного расширения воздуха:1 – капилляр; 2 - шкала для измерения положения ртутной капли; 3 - термометр; 4, 5- стеклянные сосуды.
В капилляре 1, запаянном с одного конца, используется расширение объема воздуха, заключенного между слоем серной кислоты (H2SO4) и ртутной каплей (Нg). Серная кислота служит для осушения воздуха. К капилляру прикреплена металлическая шкала 2, по которой снимают показания. Капилляр и термометр 3 помещают в стеклянный сосуд 4, в который наливается горячая вода. Капилляр соединен с вместительным стеклянным сосудом 5, что позволяет считать давление газа в опыте постоянным.
Порядок выполнения работы
1. Нагретую на электроплитке примерно до 800С воду залить в стеклянный сосуд (нижний отвод перекрыт зажимом). В сосуд вставить трубку с капилляром и термометром. Когда показания термометра установятся, измерить величину столбика воздуха ℓ (в мм) между серной кислотой и ртутью. Затем по мере остывания воды на каждые 100 повторять измерения, пока вода не остынет (значения при комнатной температуре следует снять до заливки горячей воды). Данные измерений занести в таблицу 1.
Таблица 1.
| Т,0С | |||||||
| ℓ, мм |
2. По полученным результатам построить график, откладывая по оси абсцисс значения Т,0С , а по оси ординат - соответствующее им значение ℓn ℓ. Тангенс угла наклона этой кривой (на каждом участке измерения параметров Т и ℓ) определяет значение αi при каждой измеренной температуре.
3. Построить график зависимости αi = f(1/Ti) по полученным в эксперименте значениям α, и сравнить с коэффициентом α для идеального газа, построив график α = (1/Ti) для тех же температур. Объяснить причину расхождения теории и эксперимента.
4. Контрольные вопросы
1. Какие законы определяют поведение идеального газа. Приведите математическую формулировку этих законов. Начертите график этих процессов в системе координат (Р, V).
2. Почему нагретая медицинская банка «присасывается» к телу человека?
3. Определить наименьшее возможное давление идеального газа в процессе, происходящем по закону Т = То+ КV2, где Т0 и К – положительные постоянные, V – объем одного моля газа. Изобразить примерный график этого процесса в параметрах Р, V.
4. Открытую с обеих сторон узкую цилиндрическую трубку длиной 80 см до половины погружают в ртуть. Затем закрывают верхнее отверстие трубки и вынимают ее из ртути. При этом в трубке остается столбик ртути длиной 22 см. Чему равно атмосферное давление?
5. Какая доля объема заполнится водой, если перевернутый стакан погрузить в воду на 5 м? Изменения температуры не учитывать.
6. Сосуд объемом V = 20 л содержит смесь водорода и гелия при температуре t = 200С и давлении 2 атм. Масса смеси m = 5 г. Найти отношение массы водорода к массе гелия в данной смеси.
7. Вывести зависимость от температуры коэффициента объемного расширения для идеального газа и газа Ван-дер-Ваальса. Сравнить полученные выражения.
ЛАБОРАТОРНАЯ РАБОТА 1-3
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА МЕТОДОМ КЛЕМАНА – ДЕЗОРМА
1. Цель работы
Целью работы является ознакомление с газовыми законами и с методикой определения отношения СР/СV методом адиабатического расширения (Клемана-Дезорма).
Теоретические пояснения
Процессы, которые происходят в газах, подчиняется одному из основных законов природы - закону сохранения и превращения энергии. Выражением этого закона является первое начало термодинамики. В достаточно общей форме оно может быть сформулировано так: количество теплоты δQ, сообщенное системе, расходуется на увеличение внутренней энергии системы dUи насовершение системой работы δА против внешних сил:
δQ = dU + δА (1)
Количеством теплоты называется энергия, передаваемая от одного тела к другому в процессе теплообмена.
Внутренней энергией можно назвать кинетическую и потенциальную энергию (энергию взаимодействия) его молекул.
Газ, обладающий такими же свойствами, как и совокупность невзаимодействующих материальных точек, называют идеальным газом.
Многочисленные опыты показали, что реальные газы при не слишком низких температурах и достаточно малых давлениях по своим свойствам близки к идеальным газам. Так, водород и гелий уже при атмосферном давлении и комнатной температуре ведут себя практически как идеальные газы.
Состояние газообразной системы определяется заданием трех термодинамических параметров Р, V и Т, связанных между собой уравнением состояния (для идеального газа – это уравнение Менделеева-Клапейрона):
ƒ (P,V,T) = 0. (2)
Среди процессов, которые могут происходить в газах, встречаются так называемые изопроцессы, при которых один их трех параметров состояния (Р, V или Т) сохраняется постоянным. Такими процессами являются изобарный, изохорный и изотермический.
Изохорическим (изохорным)называется процесс, когда система переходит из одного состояния в другое при постоянном объеме.
Изобарическим (изобарным) называется процесс, когда система переходит из одного состояния в другое при постоянном давлении.
Изотермическим называется процесс, когда система переходит из одного состояния в другое при постоянной температуре.
Если веществу сообщить количество тепла δQ, то его температура увеличится на dТ. Отношение бесконечно малого количества теплоты, полученного веществом, к соответствующему приращению его температуры называется теплоемкостью вещества:
C = δQ/ dТ(3)
Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью:
Сm= (1/m)С.
Так как система может быть нагрета в результате различных процессов, необходимо еще указать условия, при которых происходит нагрв. У газа различают теплоемкость при постоянном объеме CVи теплоемкость при постоянном давлении СP.
При постоянном объеме работа внешних сил δА = P dV равна нулю, и всё сообщаемое газу извне количество теплоты целиком идет на увеличение его внутренней энергии U.Отсюда теплоемкость газа при постоянном объеме СV численно равна отношению приращения внутренней энергии одного моля газа dUк приращению его температуры dT.
Cv = (∂U/∂T)V (4)
При нагревании газа при постоянном давлении газ расширяется, сообщаемое ему извне количество теплоты идет не только на увеличение его внутренней энергии, но и на совершение работы δАпротив внешних сил. Следовательно, теплоемкость газа при постоянном давлении больше теплоемкости при постоянном объеме на величину отношения работы (для идеального газа внутренняя энергия является функцией только температуры), которую совершает один моль газа при расширении, к приращению его температуры
СP = (δQ/ dТ)P = (∂U/∂T)P + Р(∂V/∂T)P (5)
Для моля идеального газа уравнение (2) имеет вид: PV = RT.Тогда в уравнении (5) (∂V/∂T)P = R/P. В результате получается уравнение Роберта Майера:
СP – СV = R.
Знание теплоемкостей СP, СV важно при рассмотрении адиабатических процессов.
Адиабатическим называется такой процесс, при котором система переходит из одного состояния в другое без теплообмена с внешней средой (например, достаточно быстрое расширение или сжатие газа).
Если в идеальном газе происходит адиабатический процесс, то
давление Ри объем V связаны уравнением Пуассона (уравнение
адиабаты)
PV γ = const, γ = СР/СV, (6)
где показатель адиабаты γесть отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме.
Для идеального газа γ может быть рассчитана теоретически, если воспользоваться постулатом о равнораспределении энергии по степеням свободы (для системы, находящейся в тепловом равновесии при температуре Т).
Числом степеней свободы iтела называется число независимых координат, которые необходимо задавать для того, чтобы полностью определить положение тела в пространстве.
Материальная точка, произвольно движущаяся в пространстве, обладает тремя степенями свободы (X, У, Z). Молекулы одноатомного газа можно рассматривать как материальные точки на том основании, что их масса сосредоточена в ядре, размеры которого очень малы (10-13 см). Молекула одноатомного газа может иметь лишь три степени свободы поступательного движения.
Молекулы, состоящие из двух, трех и более числа атомов, не могут быть уподоблены материальным точкам. Молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга. Такая молекула, помимо трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения вокруг осей X и Y (рис. 1). Вращение вокруг оси Z рассматривать не следует, т.к. предполагается, что атомы не имеют размеров.
 Z
Z
 | |||
 | |||

 У
У
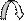 |
X
Рис. 1. Модель двухатомной молекулы с двумя степенями свободы вращения вокруг осей X и Y.
Молекулы, состоящие из трех и более атомов, не расположенных на одной прямой, обладают шестью степенями свободы: три от поступательного движения и три от вращения вокруг трех взаимно перпендикулярных осей.
Согласно теореме о равнораспределении энергии по степеням свободы, на каждую степень свободы системы приходится одинаковая кинетическая энергия:
EК = ½ kТ
где k = 1,38·10-23 Дж/К – постоянная Больцмана.
В идеальном газе нет сил взаимодействия между молекулами, а, следовательно, равна нулю и их взаимная потенциальная энергия. Таким образом, на одну степень свободы молекулы идеального газа приходится энергия E = ½ kТ, а на i степеней свободы Ei = ( i/2) kТ.
Для моля идеального газа внутренняя энергия U = (1/2) kТNА, где NА = 6,02*1023 моль -1 – число Авогадро.
Тогда, учитывая, что kNА= R, где R = 8,31 Дж/K моль – универсальная газовая постоянная, получаем:
U = (i/2)RT.
Зная аналитическое выражение для U,получаем значение CV для идеального газа:
CV = (i/2)R (7)
Используя уравнение Майера CP – CV = R, получаем выражение для CP:
CP = R (i+2)/2 . (8)
Тогда для γ:
γ = CP / CV = (i+2)/i (9)
Для воздуха, состоящего из смеси двухатомных газов N2 и O2 , i = 5, откуда γ = 1,4.
