Примеры расчета схем с индуктивно–связанными элементами
Пример 8.1
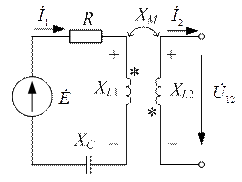
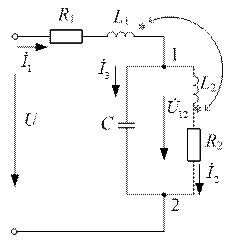 | Для цепи (рис. 8.9) определить токи во всех ветвях и напряжение 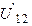 . Параметры цепи: . Параметры цепи: 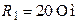 ; ; 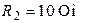 ; ; 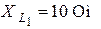 ; ; 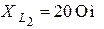 ; ; 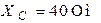 ; ; 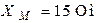 . Напряжение, приложенное к цепи . Напряжение, приложенное к цепи 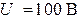 . . |
| Рис. 8.9 |
Решение
Составим уравнение по законам Кирхгофа в комплексной форме:
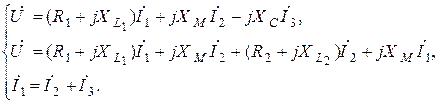 | |
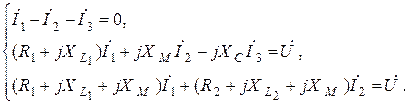 | (8.1) |
Подставляем заданные величины в (8.1) получим:
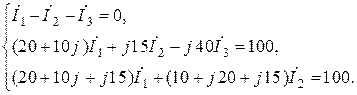 | (8.2) |
Решив систему 8.2 получим:
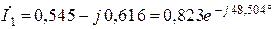 ;
;
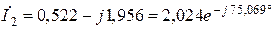 ;
;
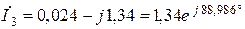 ;
;
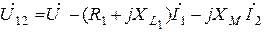 ;
;
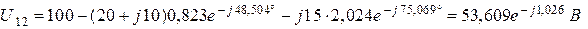 .
.
Ответ: 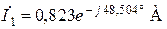 ,
, 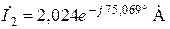 ,
, 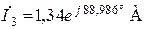 ,
, 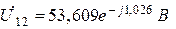 .
.
Пример 8.2
Для цепи (рис. 8.10), определить приложенное к цепи напряжение и построить топографическую диаграмму, если известно, что 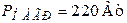 ;
; 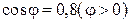 ;
; 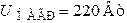 ;
; 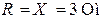 ;
; 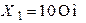 ;
; 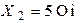 ;
; 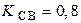 .
.
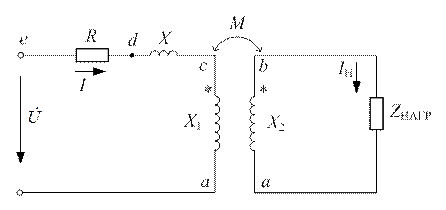 |
| Рис. 8.10 |
Решение
Уравнение, описывающее цепь, запишем в комплексной форме:
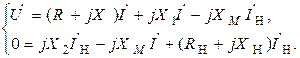 | (8.3) |
 Чтобы определить приложенное е цепи напряжение, необходимо прежде всего определить токи первичной цепи и вторичной
Чтобы определить приложенное е цепи напряжение, необходимо прежде всего определить токи первичной цепи и вторичной 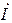 и
и 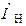 . Рассматривая второе уравнение и условие задачи, определим сначала
. Рассматривая второе уравнение и условие задачи, определим сначала 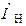 , а затем
, а затем 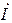 .
.
Определяем действующее значение тока нагрузки 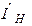 :
:
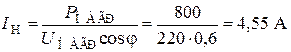 .
.
Определяем параметры нагрузки 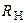 и
и 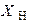 :
:
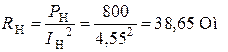 ;
;
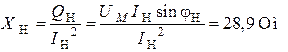 .
.
Сопротивление индуктивной связи:
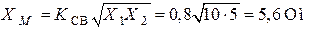 .
.
Приняв начальную фазу тока нагрузки равной 0, получим из 2–го уравнения ток первичной цепи
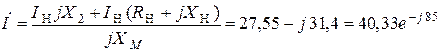 .
.
Подставляя значение 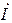 в первое уравнение системы (8.3), определяем входное напряжение
в первое уравнение системы (8.3), определяем входное напряжение 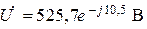 .
.
Строим топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов. Для каждого контура трансформатора строится своя диаграмма, но между ними существует связь, отображающая наличие явления взаимоиндукции. Напряжения взаимоиндукции должны быть перпендикулярны токам, которые их создают.
Выберем масштаб напряжений: 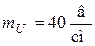 .
.
Рассчитаем действующие значения отдельных участков первичного и вторичного контуров:
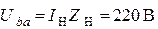 по условию задачи, это же напряжение с учетом взаимоиндукции рассчитать следующим образом
по условию задачи, это же напряжение с учетом взаимоиндукции рассчитать следующим образом
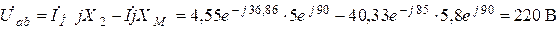 ;
;
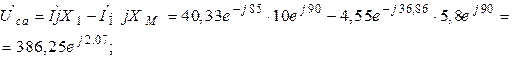
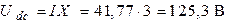 ;
;
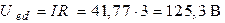 .
.
Построение начинаем с векторов токов (рис. 8.11). Затем откладываем вектор напряжения 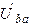 . И по условию задачи и по расчету он имеет нулевую начальную фазу.
. И по условию задачи и по расчету он имеет нулевую начальную фазу.
Строим вектора напряжений первичного контура по рассчитанным значениям. Построение начинаем из точки «a». При построении векторов 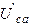 и
и 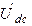 учитываем то, что напряжение на индуктивности опережает ток на
учитываем то, что напряжение на индуктивности опережает ток на 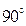 ; а напряжение на резисторе
; а напряжение на резисторе 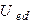 совпадает по фазе с током
совпадает по фазе с током 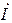 . Соединив точку «a» с точкой «е» получаем вектор входного напряжения
. Соединив точку «a» с точкой «е» получаем вектор входного напряжения 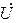 .
.
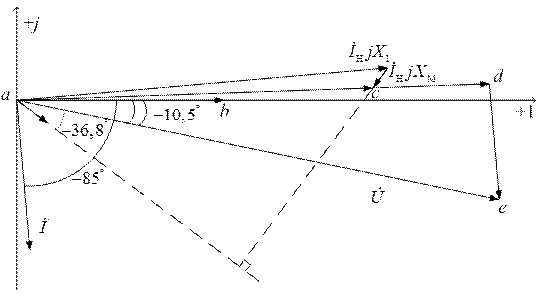 |
| Рис. 8.11 |
Пример 8.3
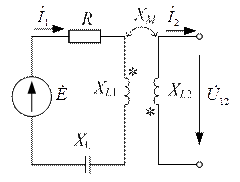 | Дано: 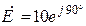 ; ; 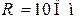 ; ; 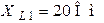 ; ; 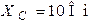 ; ; 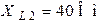 ; ; 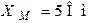 . Определить напряжение . Определить напряжение 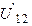 и записать его мгновенное значение. и записать его мгновенное значение. |
| Рис. 8.12 |
Решение
Поскольку на выходе трансформатора (рис. 8.12) отсутствует нагрузка 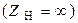 , ток во вторичной обмотке равен нулю:
, ток во вторичной обмотке равен нулю: 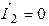 . Такой режим работы трансформатора (без нагрузки) называется режимом холостого хода.
. Такой режим работы трансформатора (без нагрузки) называется режимом холостого хода.
В катушке индуктивности 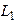 будет наводиться только ЭДС самоиндукции.
будет наводиться только ЭДС самоиндукции.
Определим ток 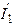 в первичной обмотке:
в первичной обмотке:
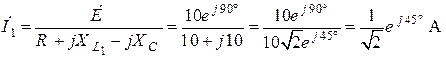 .
.
Так как ток 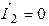 , определять тип включения индуктивно связанных элементов будем по падению напряжений на этих элементах (рис. 8.13).
, определять тип включения индуктивно связанных элементов будем по падению напряжений на этих элементах (рис. 8.13).
 | Поскольку полярности одноименных зажимов индуктивностей 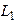 и и 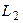 противоположны, то включение катушек является встречным. Определим напряжение противоположны, то включение катушек является встречным. Определим напряжение 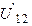 : : 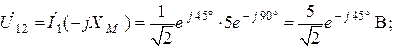 Запишем мгновенное значение напряжения Запишем мгновенное значение напряжения 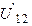 : : 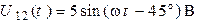 . . |
| Рис. 8.13 |
Ответ: 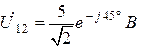 ,
, 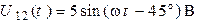 .
.
Пример 8.4
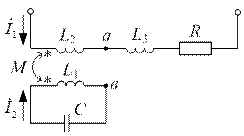 | Дано: 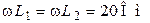 ; ; 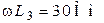 ; ; 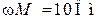 ; ; 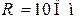 ; ; 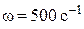 . Определить: ёмкость . Определить: ёмкость 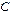 , при которой вся цепь (рис. 8.14) настроена в резонанс. , при которой вся цепь (рис. 8.14) настроена в резонанс. |
| Рис. 8.14 |
Решение
Произведём развязку индуктивной связи (рис. 8.15).
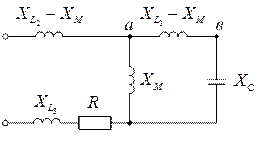 |
| Рис. 8.15 |
Условием возникновения резонанса является равенство нулю мнимой части эквивалентного комплексного сопротивления цепи:
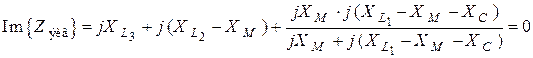 .
.
Подставив в последнее выражение численные значения, получаем:
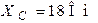 ;
; 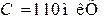 .
.
Ответ: 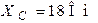 ;
; 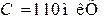 .
.
Задачи для самоконтроля
Задача №1
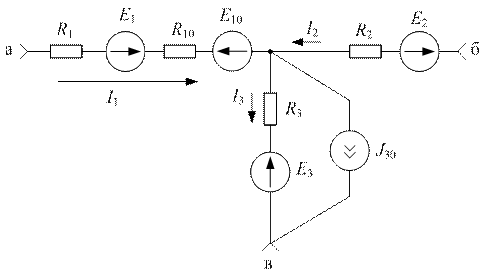 |
Дано:
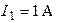 ;
; 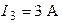 ;
; 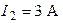 ;
; 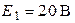 ;
; 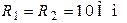 ;
; 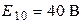 ;
; 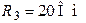 ;
; 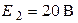 ;
; 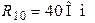 ;
; 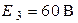 ;
; 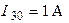 . Определить напряжение между узлами:
. Определить напряжение между узлами: 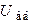 ,
, 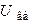 ,
, 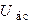 ,
, 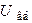 .
.
Ответ: 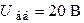 ;
; 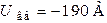 ;
; 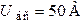 ;
; 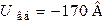 .
.
Задача №2
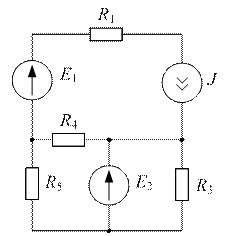 | Дано: 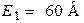 ; ; 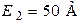 ; ; 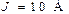 ; ; 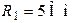 ; ; 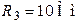 ; ; 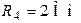 ; ; 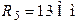 . Определить токи, используя метод наложения. Ответ: . Определить токи, используя метод наложения. Ответ: 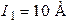 ; ; 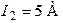 ; ; 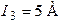 ; ; 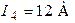 ; ; 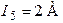 ; ; 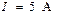 . . |
Задача №3
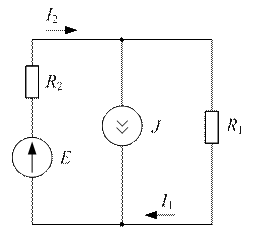 | Дано: 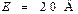 ; ; 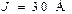 ; ; 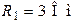 ; ; 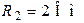 . Определить токи методом двух узлов. Ответ: –8 А; 22 А. . Определить токи методом двух узлов. Ответ: –8 А; 22 А. |
Задача №4
Найти токи I1; I2 в цепи задачи №3:
1. предварительно преобразовав Э.Д.С. в источник тока;
2. предварительно преобразовав источник тока в источник Э.Д.С.
Показать, что в п.п.1 и 2 мощности, отдаваемые источниками E и J, нельзя определить как мощности источников после преобразования цепи.
Задача №5
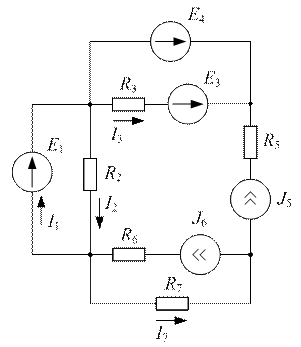 | Дано: 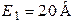 ; ; 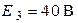 ; ; 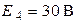 ; ; 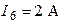 ; ; 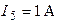 ; ; 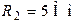 ; ; 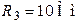 ; ; 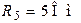 ; ; 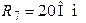 ; ; 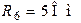 . Определить токи в схеме Составить и рассчитать баланс мощностей. Ответы: . Определить токи в схеме Составить и рассчитать баланс мощностей. Ответы: 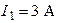 ; ; 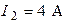 ; ; 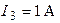 ; ; 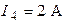 ; ; 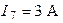 ; ; 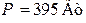 . . |
Задача №6
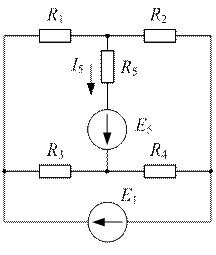 | Дано: 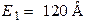 ; ; 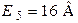 ; ; 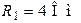 ; ; 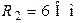 ; ; 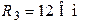 ; ; 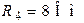 ; ; 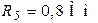 . Определить ток I5 по методу эквивалентного генератора напряжения. Ответ: . Определить ток I5 по методу эквивалентного генератора напряжения. Ответ: 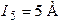 . . |
Задача №7
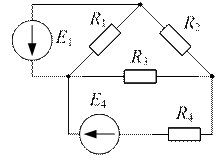 | Дано: 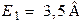 ; ; 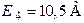 ; ; 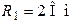 ; ; 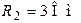 ; ; 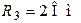 ; ; 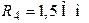 ; ; 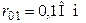 ; ; 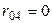 . Определить ток I4 по методу эквивалентного генератора. Ответ: . Определить ток I4 по методу эквивалентного генератора. Ответ: 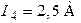 . . |
Задача №8
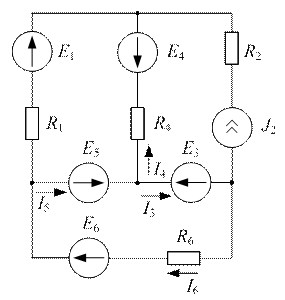 | Дано: 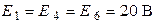 ; ; 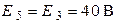 ; ; 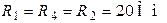 ; ; 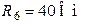 ; ; 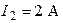 . Определить ток . Определить ток 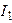 методом эквивалентного генератора напряжения. Ответ: методом эквивалентного генератора напряжения. Ответ: 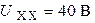 ; ; 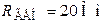 ; ; 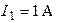 . . |
Задача №9
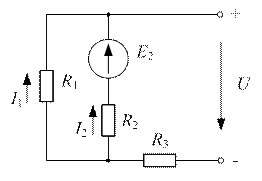 | Дано: 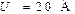 ; ; 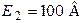 ; ; 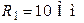 ; ; 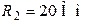 . Определить все токи, используя законы Кирхгофа. Ответ: . Определить все токи, используя законы Кирхгофа. Ответ: 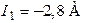 ; ; 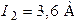 ; ; 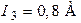 . . |
Задача №10
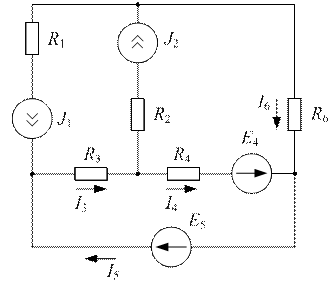 | Дано: 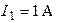 ; ; 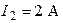 ; ; 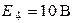 ; ; 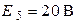 ; ; 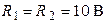 ; ; 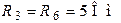 ; ; 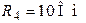 . Определить токи в схеме. Составить и рассчитать баланс мощностей. Ответы: . Определить токи в схеме. Составить и рассчитать баланс мощностей. Ответы: 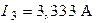 ; ; 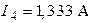 ; ; 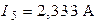 ; ; 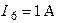 ; ; 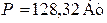 . . |
Задача №11
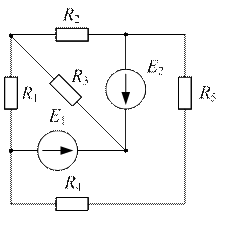 | Дано: 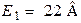 ; ; 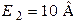 ; ; 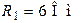 ; ; 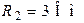 ; ; 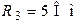 ; ; 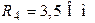 ; ; 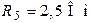 . Определить ток . Определить ток 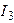 по методу эквивалентного генератора напряжения. Ответ: по методу эквивалентного генератора напряжения. Ответ: 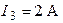 . . |
Задача №12
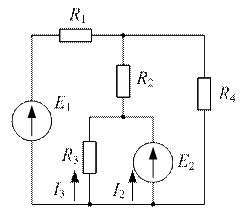 | Дано: 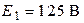 ; ; 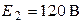 ; ; 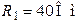 ; ; 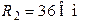 ; ; 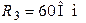 ; ; 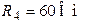 . Определить ток . Определить ток 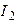 по методу наложения. Ответ: по методу наложения. Ответ: 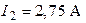 . . |
Задача №13
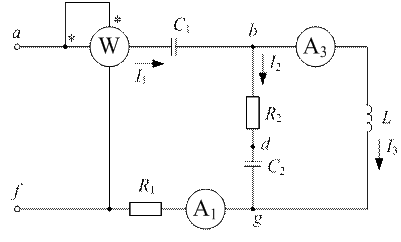 | Дано: 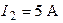 ; ; 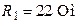 ; ; 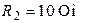 ; ; 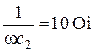 ; ; 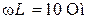 . . |
Определить напряжение на входе и показания приборов:
1)построив топографическую диаграмму напряжений и векторную диаграмму токов без аналитического расчета цепи комплексным методом
2)расчетным методом
Ответ: 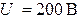 ;
; 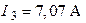 ;
; 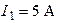 ;
; 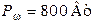 .
.
Задача №14
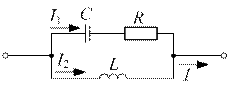 | Цепь находится в режиме резонанса; при этом токи 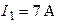 ; ; 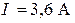 . Определить ток . Определить ток 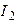 . Построить векторную диаграмму. . Построить векторную диаграмму. |
Ответ: 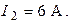
Задача №15
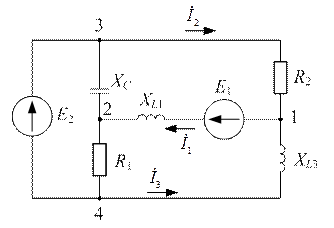 | Дано: 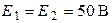 ; Э.Д.С. ; Э.Д.С. 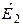 отстает по фазе от Э.Д.С. отстает по фазе от Э.Д.С. 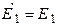 на на 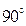 . Определить: 1)комплекс тока . Определить: 1)комплекс тока 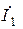 по теореме об эквивалентном генераторе напряжения. 2)зная ток по теореме об эквивалентном генераторе напряжения. 2)зная ток 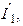 найти найти 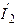 и и 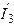 . . |
3)построить топографическую диаграмму для режима, когда ветвь с Э.Д.С. 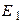 отключена и найти по диаграмме
отключена и найти по диаграмме 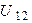 .
.
Ответ: 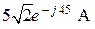 ;
; 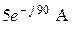 ;
; 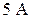 ;
; 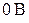 .
.
Задача №16
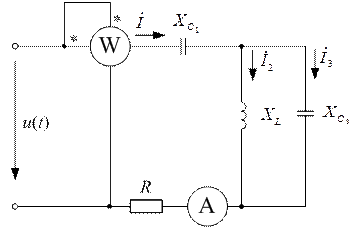 | Дано: 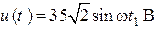 ; ; 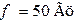 ; ; 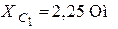 ; ; 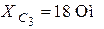 ; ; 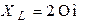 ; ; 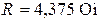 . Определить показания приборов; токи . Определить показания приборов; токи 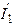 , , 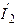 ; напряжения на емкостях. Построить векторную диаграмму токов и напряжений. ; напряжения на емкостях. Построить векторную диаграмму токов и напряжений. |
Ответ: 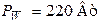 ;
; 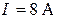 ;
; 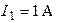 ;
; 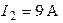 ;
; 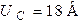 .
.
Задача №17
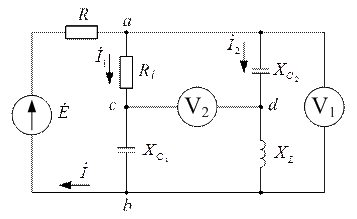 | Дано: 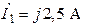 ; ; 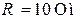 ; ; 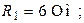 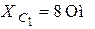 ; ; 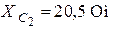 ; ; 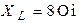 . 1)построить топографическую диаграмму и найти по ней показания вольтметров. . 1)построить топографическую диаграмму и найти по ней показания вольтметров. |
2)применяя свойства линейности, найти показания вольтметра при Э.Д.С. 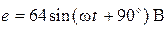 .
.
Ответ: 1) 25 В; 34,2 В. 2) 20 В; 27,4 В.
Задача №18
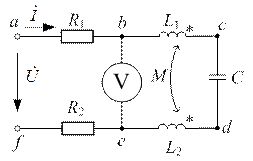 | Дано: 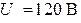 ; ; 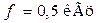 ; ; 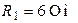 ; ; 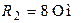 ; ; 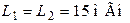 ; ; 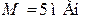 . Определить при какой емкости С в цепи будет резонанс. Для режима резонанса построить топографическую диаграмму и найти показания вольтметра. . Определить при какой емкости С в цепи будет резонанс. Для режима резонанса построить топографическую диаграмму и найти показания вольтметра. |
Ответ: 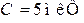 ;
; 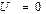 .
. 
Задача №19
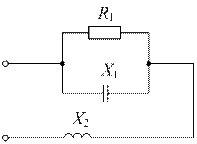 | Дано: 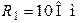 , , 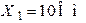 . Определить, при каком значении сопротивления . Определить, при каком значении сопротивления 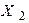 в цепи наступит резонанс напряжений. в цепи наступит резонанс напряжений. |
Ответ: 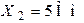 .
.
Задача №20
Определить сопротивление потерь последовательного колебательного контура, если известно, что 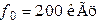 ,
, 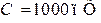 , абсолютная полоса пропускания
, абсолютная полоса пропускания 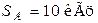 .
.
Ответ: 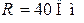 .
.
Задача № 21
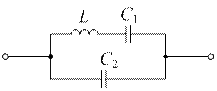 | Дано: контур находится в режиме резонанса токов. Определить резонансную частоту контура, если 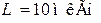 , , 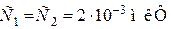 Ответ: Ответ: |
Задача №22
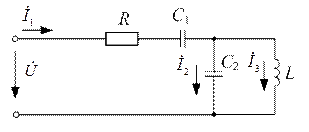 | Дано: 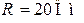 , , 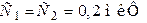 , , 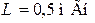 , , 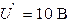 . . |
Определить:
1. Резонансные частоты цепи.
2. Определить токи 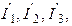 при резонансе напряжений.
при резонансе напряжений.
Ответ:
Задача №23
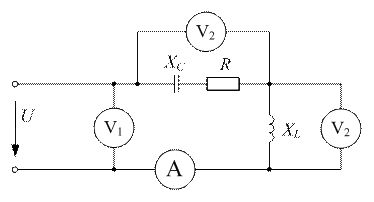 | В цепи резонанс напряжений. Приборы показали: 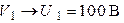 ; ; 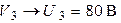 ; ; 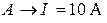 . . |
Определить показания вольтметра 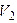 , а также параметры цепи
, а также параметры цепи 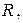
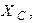
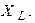
Ответ:
Задача №24
Определить: 1) ток 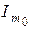 (в
(в 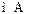 ); 2) амплитуду ЭДС (в
); 2) амплитуду ЭДС (в 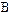 ) последовательного колебательного контура, настроенного в резонанс, если мощность, отдаваемая источником ЭДС в настроенный контур,
) последовательного колебательного контура, настроенного в резонанс, если мощность, отдаваемая источником ЭДС в настроенный контур, 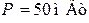 ;
; 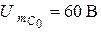 ;
; 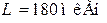 ;
; 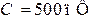 .
.
Ответ: 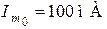 ;
; 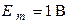 .
.
Задача №25
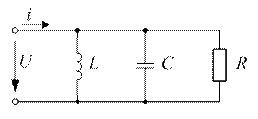 | Определить мгновенное значение тока  в неразветвлённой части схемы замещения параллельного колебательного контура, если в неразветвлённой части схемы замещения параллельного колебательного контура, если 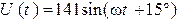 , , 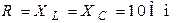 . . |
Задача №26
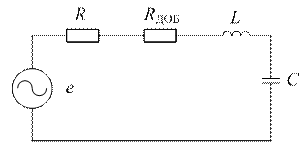 | Дано: 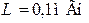 ; ; 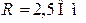 ; ; 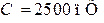 ; ; 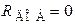 ; Определить: 1) характеристическое сопротивление (в ; Определить: 1) характеристическое сопротивление (в 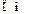 ) ) |
2) добавочное сопротивление 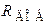 (в
(в 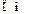 ), при котором полоса пропускания увеличится в 3 раза (
), при котором полоса пропускания увеличится в 3 раза ( 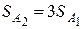 ).
).
Ответ: 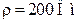 ;
; 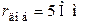 .
.
Задача №27
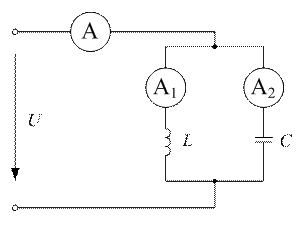 | В цепи наблюдается резонанс токов. Амперметр 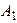 показывает ток показывает ток 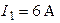 , амперметр , амперметр 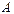 показывает ток показывает ток 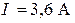 . Определить показание амперметра . Определить показание амперметра 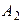 . Ответ: . Ответ: 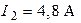 . . |
Задача №28
Что покажет амперметр в цепи задачи 24, если показания амперметров 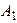 и
и 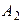 одинаковые:
одинаковые: 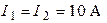 .
.
Задача №29
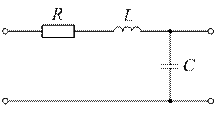 | При резонансе ток в цепи равен 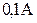 , при напряжении на входе , при напряжении на входе 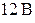 . Добротность контура . Добротность контура 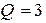 . Определить напряжение на всех элементах и ток в цепи при . Определить напряжение на всех элементах и ток в цепи при 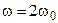 и том же напряжении на входе цепи. и том же напряжении на входе цепи. |
Ответ: 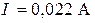 ;
; 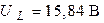 ;
; 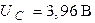 .
.
Задача №30
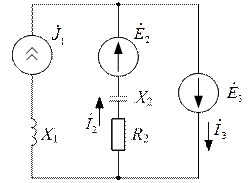 | Дано: 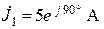 ; ; 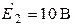 ; ; 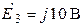 ; ; 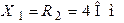 ; ; 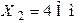 . Определить токи в схеме. Составить и рассчитать баланс мощностей. Ответы: . Определить токи в схеме. Составить и рассчитать баланс мощностей. Ответы: 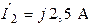 ; ; 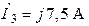 ; ; 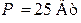 ; ; 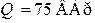 . . |
Задача №31e
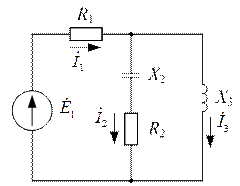 | Дано: 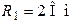 ; ; 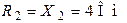 ; ; 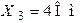 ; ; 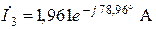 . Определить величину источника ЭДС . Определить величину источника ЭДС 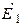 . Ответ: . Ответ: 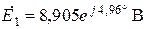 . . |
Задача №32
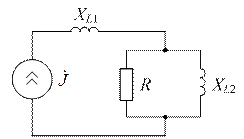 | Дано: 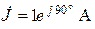 ; ; 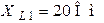 ; ; 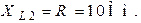 Составить и рассчитать баланс мощностей. Ответ: Составить и рассчитать баланс мощностей. Ответ: 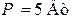 ; ; 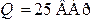 . . |
Задача №33
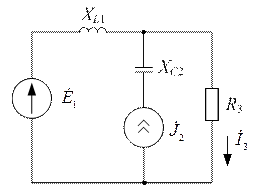 | Дано: 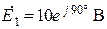 ; ; 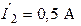 ; ; 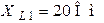 ; ; 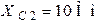 ; ; 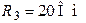 . Определить ток . Определить ток 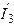 МЭГН и записать его мгновенное значение. Ответ: МЭГН и записать его мгновенное значение. Ответ: 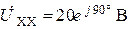 ; ; 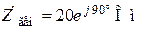 ; ; 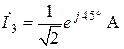 ; ; 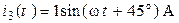 . . |
Задача №34
Напряжение на входе схем рис. 11.1 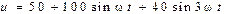 В. Сопротивления для основной гармоники
В. Сопротивления для основной гармоники 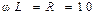 (Ом);
(Ом); 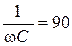 Ом.
Ом.
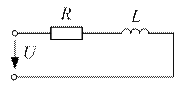
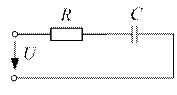
а б
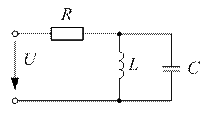
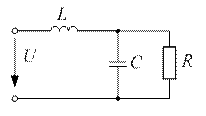
вг
Рис. 11.1
Определить действующие значения тока источника и реактивную мощность цепи (рис.11.1).
Ответ: а) 7,13 А; 274 ВАр, б) 1,19 А; -79 ВАр, в) 6,85А; 247 ВАр,
г) 7,35 А; 278 ВАр.
Задача №35
К зажимам цепи (рис 11.2) подведено напряжение: 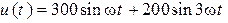 ,В. Параметры цепи:
,В. Параметры цепи: 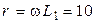 Ом,
Ом, 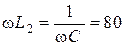 Ом. Определить действующие значения всех токов и мгновенное значение напряжения между точками 1 и 2.
Ом. Определить действующие значения всех токов и мгновенное значение напряжения между точками 1 и 2.
Ответ: 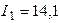 А,
А, 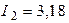 А,
А, 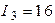 А,
А, 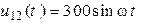 В.
В.
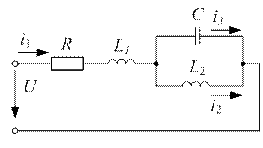
Рис. 11.2
Задача №36
В неразветвлённой электрической цепи переменного тока протекает периодический несинусоидальный ток 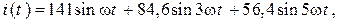 А. Определить действующее значение несинусоидального тока.
А. Определить действующее значение несинусоидального тока.
Ответ: I =123,29 А.
Задача №37
В схеме рис. 11.3 определить показания приборов, если 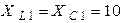 Ом,
Ом, 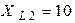 Ом,
Ом, 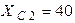 Ом,
Ом, 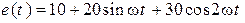 В.
В.
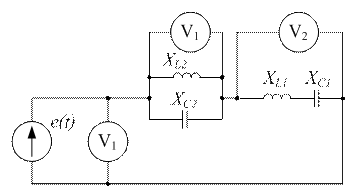
Рис. 11.3
Ответ: 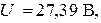
Задача №38
Дано: 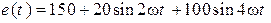 В,
В, 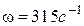 ,
, 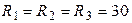 Ом,
Ом,
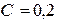 мкФ,
мкФ, 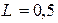 Гн. Схема представлена на рис. 11.4.
Гн. Схема представлена на рис. 11.4.
Определить: 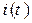 ,
, 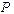 ,
, 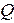 - ?
- ?
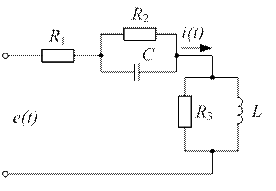
Рис. 11.4
Задача №39
Дано: 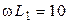 Ом
Ом 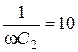 Ом,
Ом, 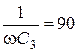 Ом,
Ом, 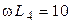 Ом
Ом
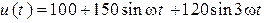 В .
В .
Определить показания приборов электродинамической системы (рис.11.5).
Ответ: U1=100 B, U2=137, 6 B, I3= 3 A.

Рис. 11.5
Задача №40
Для схемы на рис. 11.6 определить 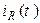 , если:
, если:
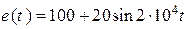 В,
В, 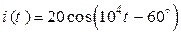 А,
А, 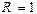 Ом,
Ом,
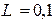 мГн,
мГн, 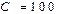 мкФ.
мкФ.
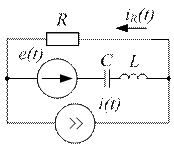
Рис. 11.6
Задача №41
Дано: R=10 Ом, 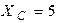 Ом,
Ом, 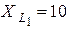 Ом,
Ом, 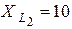 Ом,
Ом, 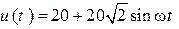 (В),
(В), 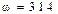 (рад/сек.) . Схема представлена на рис. 11.7. Определить
(рад/сек.) . Схема представлена на рис. 11.7. Определить 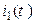 ,
, 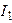 ,
, 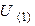 .
.
Ответ: 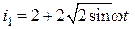 А,
А, 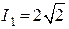 А,
А, 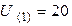 В.
В.
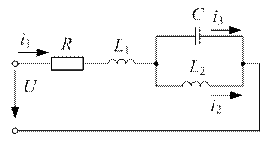
Рис. 11.7
Задача № 42
Определить токи в трёхфазной цепи, если линейные напряжения на входе в цепь симметричны 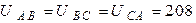 В, а комплексные сопротивления фаз
В, а комплексные сопротивления фаз 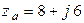 Ом,
Ом, 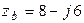 Ом,
Ом, 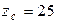 Ом. Построить векторную диаграмму.
Ом. Построить векторную диаграмму.
Ответ: 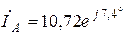 ;
; 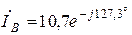 ;
; 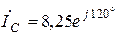 .
.
Задача№ 43
К трёхфазной линии, линейные напряжения которой симметричны 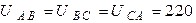 В, присоединены три приёмника энергии по схеме треугольник. Комплексные сопротивления этих приёмников
В, присоединены три приёмника энергии по схеме треугольник. Комплексные сопротивления этих приёмников 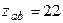 Ом;
Ом; 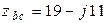 Ом;
Ом; 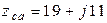 Ом. Определить линейные и фазные токи цепи и построить векторную диаграмму.
Ом. Определить линейные и фазные токи цепи и построить векторную диаграмму.
Ответ: 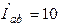 А,
А, 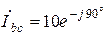 А,
А, 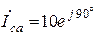 А,
А, 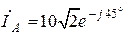 А,
А,
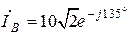 А,
А, 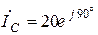 А.
А.
Задача № 44
К зажимам четырехпроводной сети с фазным напряжением 127В подключён несимметричный приёмник, сопротивление фаз которого 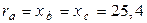 Ом. Определить фазные токи приёмника и ток в нейтральном проводе. Построить векторную диаграмму.
Ом. Определить фазные токи приёмника и ток в нейтральном проводе. Построить векторную диаграмму.
Ответ: 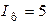 А;
А; 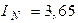 А.
А.
Задача № 45
Несимметричный трёхфазный приёмник, включенный по схеме «звезда» с нейтральным проводом сопротивление фаз которого 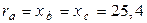 Ом (фазное напряжение генератора 127В), в номинальном режиме работы имеет фазные токи
Ом (фазное напряжение генератора 127В), в номинальном режиме работы имеет фазные токи 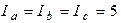 А. Определить фазные токи и напряжения приёмника при обрыве нейтрального провода. Построить векторную диаграмму.
А. Определить фазные токи и напряжения приёмника при обрыве нейтрального провода. Построить векторную диаграмму.
Ответ: 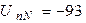 В;
В; 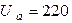 В;
В; 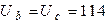 В;
В; 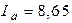 А;
А; 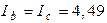 А.
А.
Задача № 46
Трёхфазный приёмник соединён звездой без нейтрального провода и присоединён к генератору, соединённому звездой, с симметричными фазными напряжениями 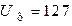 В;
В; 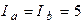 А. Качественная векторная диаграмма нагрузки представлена на рис. 11.8. Вычислить смещение нейтрали и найти сопротивления каждой фазы нагрузки.
А. Качественная векторная диаграмма нагрузки представлена на рис. 11.8. Вычислить смещение нейтрали и найти сопротивления каждой фазы нагрузки.
Ответ: 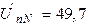 В;
В; 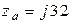 Ом;
Ом; 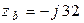 Ом;
Ом; 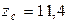 Ом.
Ом.
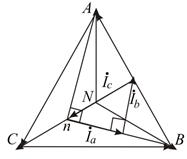
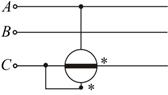
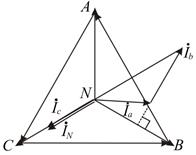
Рис. 11.8 Рис. 11.9 Рис. 11.10
Задача № 47
В цепи задачи № 46 найти показание ваттметра, включённого, как показано на рис. 11.9
Ответ: 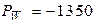 Вт.
Вт.
Задача № 48
Для задачи № 46 начертить векторную диаграмму токов после присоединения нейтрального провода ( 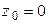 ). Найти показание ваттметра, включённого по схеме рис. 11.9.
). Найти показание ваттметра, включённого по схеме рис. 11.9.
Ответ: 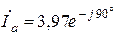 А,
А, 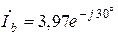 А,
А, 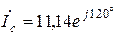 А,
А, 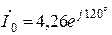 А,
А, 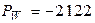 Вт.
Вт.
Экзаменационные вопросы
Часть 1
1.Электрическая цепь: основные величины элементы и понятия. Мгновенная мощность и энергия.
2.Источники электрической энергии и их взаимное преобразование.
3.Потенциальная диаграмма. Обобщённый закон Ома.
4.Метод контурных токов.
5.Применение метода контурных токов при наличии в цепи идеальных источников тока.
6.Применение законов Кирхгофа для расчета электрических цепей.
7.Метод наложения. Входные и взаимные проводимости и сопротивления.
8.Метод узловых потенциалов.
9.Применение метода узловых потенциалов при наличии в цепи идеальных источников эдс.
10.Теорема компенсации. Метод эквивалентного источника.
11.Метод преобразований.
12.Эквивалентные преобразования пассивных соединений звездой и треугольником.
13.Эквивалентные преобразования активных соединений звездой и треугольником.
14.Метод пропорционального пересчета.
15.Баланс мощностей в цепи постоянного тока.
16.Действующее и среднее значения синусоидальных функций
времени.
17.Изображение синусоидальных токов и напряжений вращающимися векторами. Векторные диаграммы.
18.Синусоидальный ток в активном сопротивлении.
19.Синусоидальный ток в индуктивности.
20.Синусоидальный ток в ёмкости.
21.Последовательная r-L-C цепь. Треугольники напряжений и сопротивлений.
22.Параллельная r-L-C цепь. Треугольники токов и проводимостей.
23.Эквивалентные параметры сложной цепи синусоидального тока.
24.Мощность в цепи синусоидального тока.
25.Графоаналитический метод расчета цепей синусоидального тока.
26.Топографическая векторная диаграмма.
27. Изображение синусоидальных функций времени, их производных и интегралов комплексными переменными.
28.Законы Ома и Кирхгофа в комплексной форме.
29.Расчёт цепи синусоидального тока символическим методом.
30.Мощность цепи синусоидального тока в комплексной форме.
31.Условие передачи максимальной мощности от источника к приемнику.
32.Баланс мощностей в цепи синусоидального тока.
33.Взаимная индуктивность. Коэффициент связи.
34.Одноименные зажимы индуктивно связанных катушек.
35.Последовательное соединение индуктивно связанных катушек при согласном включении.
36.Последовательное соединение индуктивно связанных катушек при встречном включении.
37.Расчёт индуктивно связанных цепей.
38.Развязка индуктивных связей.
39.Воздушный трансформатор.
40.Резонанс в электрических цепях.
41.Резонанс в последовательном контуре.
42.Частотные характеристики последовательного колебательного контура.
43.Частотные характеристики тока в относительных единицах.
44.Полоса пропускания последовательного колебательного контура.
45.Векторные диаграммы последовательного контура при различных соотношениях текущей и резонансной частот.
46.Резонанс в параллельном контуре.
47.Частотные характеристики параллельного колебательного контура.
48.Влияние внутреннего сопротивления источника электрической энергии на характеристики последовательного и параллельного колебательных контуров.
