Транспортная задача
Постановка задачи. Пусть имеется 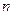 пунктов отправления (производителей или поставщиков однородной продукции)
пунктов отправления (производителей или поставщиков однородной продукции) 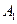 ,
, 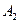 ,
, 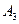 ,…,
,…, 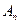 и
и 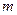 пунктов назначения (потребителей этой продукции)
пунктов назначения (потребителей этой продукции) 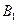 ,
, 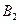 ,
, 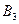 , …,
, …, 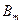 . Известны запасы
. Известны запасы 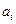 продукции у каждого поставщика
продукции у каждого поставщика 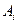 , потребности
, потребности 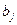 каждого потребителя
каждого потребителя 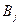 и тарифы
и тарифы 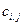 (стоимости перевозок единицы товара от пункта от
(стоимости перевозок единицы товара от пункта от 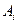 в пункт
в пункт 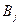 ). Требуется составить оптимальный план перевозок, то есть определить, какое количество груза
). Требуется составить оптимальный план перевозок, то есть определить, какое количество груза 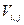 должно быть отправлено из каждого пункта отправления в каждый пункт назначения, чтобы общая стоимость всех перевозок была минимальной.
должно быть отправлено из каждого пункта отправления в каждый пункт назначения, чтобы общая стоимость всех перевозок была минимальной.
Условия задачи и её решение (план перевозок) компактным образом записываются в виде распределительной таблицы.
Распределительная таблица (тарифы, запасы и потребности)
| Поставщики | Потребители | Запасы | ||||
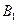 | 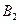 | 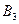 | 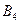 | 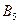 | ||
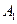 | 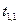 | 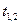 | 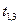 | 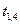 | 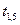 | 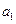 |
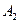 | 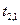 | 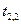 | 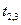 | 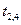 | 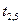 | 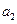 |
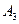 | 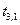 | 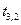 | 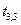 | 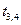 | 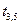 | 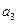 |
| Потребности | 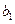 | 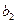 | 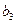 | 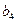 | 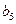 |
Если общий запас продукции (груза) у поставщиков равен общей потребности потребителей, то транспортная задача будет закрытой. В случае, когда потребности потребителей превышают возможности поставок, или когда запасы груза превышают потребности потребителей, имеем открытую транспортную задачу. Открытую транспортную задачу сводим к закрытой путём введения мнимого поставщика в первом случае, или мнимого потребителя - во втором. “Возможности поставок” мнимого поставщика или “потребности” мнимого потребителя составляют разность между общими запасами и общими потребностями. Тарифы 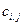 на поставку груза от мнимого поставщика реальным потребителям, или от реальных поставщиков мнимому потребителю принимаются равными нулю, так как реально груз в этом случае не поставляется.
на поставку груза от мнимого поставщика реальным потребителям, или от реальных поставщиков мнимому потребителю принимаются равными нулю, так как реально груз в этом случае не поставляется.
Кроме того, в задаче могут быть и некоторые другие ограничения. Например, могут быть привилегированные потребители, которым груз должен быть поставлен в полном объёме, или привилегированные поставщики, от которых груз должен быть вывезен полностью. Пусть в данной задаче привилегированными потребителями являются потребители 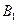 и
и 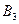 . Чтобы исключить случай, когда привилегированный потребитель не получит груз в полном объёме, тариф
. Чтобы исключить случай, когда привилегированный потребитель не получит груз в полном объёме, тариф 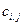 на поставку груза от мнимого поставщика к привилегированному потребителю принимаем “высоким” (
на поставку груза от мнимого поставщика к привилегированному потребителю принимаем “высоким” (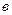 ), превышающим любой другой тариф в любое число раз.
), превышающим любой другой тариф в любое число раз.
Исходный опорный план обычно составляют или методом северо-западного угла или методом минимального элемента.
При составлении опорного плана методом северо-западного угла заполнение клеток распределительной таблицы начинается с клетки 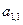 . Предусматривается поставка от первого поставщика к первому потребителю в максимальном объёме (или до удовлетворения потребностей первого потребителя, или до исчерпания возможностей первого поставщика). Далее заполняются клетки, расположенные вблизи диагонали таблицы. Заканчивается составление опорного плана в правом нижнем углу таблицы
. Предусматривается поставка от первого поставщика к первому потребителю в максимальном объёме (или до удовлетворения потребностей первого потребителя, или до исчерпания возможностей первого поставщика). Далее заполняются клетки, расположенные вблизи диагонали таблицы. Заканчивается составление опорного плана в правом нижнем углу таблицы 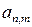 .
.
Ниже приводится пример составления опорного плана методом северо-западного угла.
Планируем поставку от поставщика 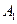 потребителю
потребителю 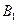 до удовлетворения его потребности в грузе. Остаток запаса груза у первого поставщика поставляем второму потребителю. Так как второму потребителю необходимо большее количество груза, чем осталось у первого поставщика, то недостающую часть груза ему поставляет второй поставщик. Остаток груза после поставки второму потребителю второй поставщик поставляет третьему потребителю и т.д. Заканчивается построение исходного опорного плана методом северо-западного угла заполнением клетки
до удовлетворения его потребности в грузе. Остаток запаса груза у первого поставщика поставляем второму потребителю. Так как второму потребителю необходимо большее количество груза, чем осталось у первого поставщика, то недостающую часть груза ему поставляет второй поставщик. Остаток груза после поставки второму потребителю второй поставщик поставляет третьему потребителю и т.д. Заканчивается построение исходного опорного плана методом северо-западного угла заполнением клетки 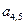 .
.
Так как при этом методе составления исходного опорного плана мы вообще не учитывали тарифы перевозок, то этот опорный план вряд ли будет оптимальным. Проверку составленного плана на оптимальность проводим методом потенциалов. Необходимо найти потенциалы всех потребителей и поставщиков. В нашем случае надо определить потенциалы четырёх поставщиков и пяти потребителей (всего 9 потенциалов).
Исходный опорный план методом северо-западного угла (нулевая итерация).
| 0 итерация | 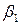 =6 =6 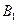 | 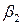 =4 =4 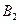 | 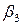 =3 =3 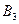 | 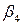 =4 =4 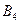 | 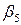 =8 =8 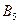 | наличие | ||||||||||
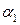 =-1 =-1 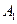 | - | + | ||||||||||||||
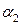 =0 =0 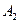 | ||||||||||||||||
| + | - | |||||||||||||||
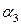 =0 =0 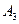 | ||||||||||||||||
| + | - | |||||||||||||||
| - | ||||||||||||||||
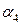 =-8 =-8 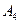 | в | в | ||||||||||||||
| -2 | -4 | -5 | ||||||||||||||
| потребность | Груза | |||||||||||||||
Для заполненных клеток сумма потенциалов поставщика 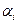 и потребителя и потребителя 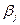 равна тарифу поставок равна тарифу поставок 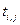 . Всего заполнено 8 клеток и можем составить только восемь уравнений для определения 9 параметров. Поэтому потенциал . Всего заполнено 8 клеток и можем составить только восемь уравнений для определения 9 параметров. Поэтому потенциал 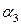 принимаем произвольно. Пусть он равен 0. Тогда: принимаем произвольно. Пусть он равен 0. Тогда: 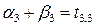 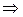 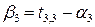 . . 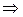 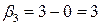 . . 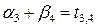 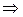 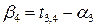 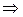 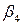 =4-0 = 4. =4-0 = 4. 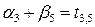 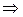 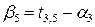 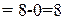 . . 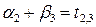 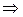 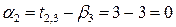 . . 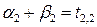 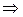 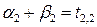 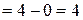 . и т.д. После нахождения потенциалов всех поставщиков и потребителей находим потенциалы свободных клеток. Потенциал свободной клетки . и т.д. После нахождения потенциалов всех поставщиков и потребителей находим потенциалы свободных клеток. Потенциал свободной клетки 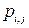 равен сумме потенциалов поставщика равен сумме потенциалов поставщика 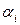 и потребителя и потребителя 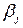 .( .( 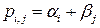 ). Потенциалы ). Потенциалы 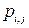 помещаем в нижнем правом углу свободных клеток. Если хотя бы для одной свободной клетки помещаем в нижнем правом углу свободных клеток. Если хотя бы для одной свободной клетки 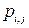 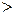 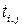 , то план не оптимальный и его следует улучшать, составляя цикл пересчёта плана. Цикл пересчёта составляется для свободной ячейки с максимальным превышением потенциала над тарифом. Цикл пересчёта представляет собой замкнутую ломаную линию, состоящую из горизонтальных и вертикальных звеньев. Вершины цикла, кроме свободной клетки, для которой составляется цикл, обязательно должны находиться в заполненных клетках. Для каждой свободной клетки можно составить цикл и притом только один. Вершинам цикла последовательно, начиная со свободной клетки, присваиваются знаки , то план не оптимальный и его следует улучшать, составляя цикл пересчёта плана. Цикл пересчёта составляется для свободной ячейки с максимальным превышением потенциала над тарифом. Цикл пересчёта представляет собой замкнутую ломаную линию, состоящую из горизонтальных и вертикальных звеньев. Вершины цикла, кроме свободной клетки, для которой составляется цикл, обязательно должны находиться в заполненных клетках. Для каждой свободной клетки можно составить цикл и притом только один. Вершинам цикла последовательно, начиная со свободной клетки, присваиваются знаки 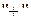 и и 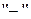 . Находится минимальное количество груза в «отрицательных» клетках и его перераспределяем по циклу, вычитая от «отрицательных» клеток и прибавляя к «положительным». В остальных клетках, не являющихся вершинами цикла, количество груза остаётся неизменным. Получим новый опорный план, (1 итерация) который также проверяем на оптимальность. Все потенциалы при этом рассчитываем заново. . Находится минимальное количество груза в «отрицательных» клетках и его перераспределяем по циклу, вычитая от «отрицательных» клеток и прибавляя к «положительным». В остальных клетках, не являющихся вершинами цикла, количество груза остаётся неизменным. Получим новый опорный план, (1 итерация) который также проверяем на оптимальность. Все потенциалы при этом рассчитываем заново. | ||||||||||||||||
| Распределительная таблица. Первая итерация. | ||||||||||||||||
| 1 итерация | 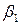 =9 =9 | 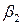 =7 =7 | 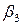 =3 =3 | 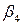 =4 =4 | 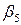 =8 =8 | наличие | ||||||||||
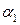 =-4 =-4 | ||||||||||||||||
| - | -1 | + | ||||||||||||||
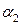 =-3 =-3 | ||||||||||||||||
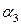 =0 =0 | ||||||||||||||||
| + | - | |||||||||||||||
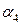 =-8 =-8 | в | в | ||||||||||||||
| -1 | -5 | -4 | ||||||||||||||
| потребность | груза |
Т.к. потенциал 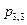 превышает тариф
превышает тариф 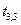 , то для свободной клетки
, то для свободной клетки 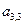 снова составляем цикл пересчёта (вторая итерация). Вершины цикла располагаются в ячейках
снова составляем цикл пересчёта (вторая итерация). Вершины цикла располагаются в ячейках 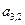 ,
, 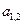 ,
, 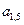 ,
,  . «Отрицательными» клетками являются клетки
. «Отрицательными» клетками являются клетки 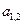 и
и  . Минимальное количество груза находится в ячейке
. Минимальное количество груза находится в ячейке 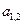 и составляет 200единиц. Это количество груза перераспределяем по циклу.Получим план второй итерации, который также не является оптимальным.
и составляет 200единиц. Это количество груза перераспределяем по циклу.Получим план второй итерации, который также не является оптимальным.
Распределительная таблица. Вторая итерация.
| 2 итерация | 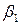 =9 =9 | 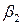 =5 =5 | 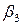 =3 =3 | 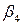 =4 =4 | 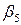 =8 =8 | наличие | ||||||||||
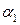 =-4 =-4 | ||||||||||||||||
| -1 | ||||||||||||||||
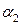 =-1 =-1 | ||||||||||||||||
| - | +2 | |||||||||||||||
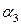 =0 =0 | ||||||||||||||||
| + | - | |||||||||||||||
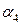 =-8 =-8 | в | в | ||||||||||||||
| -3 | -5 | -4 | ||||||||||||||
| потребность | груза |
Распределительная таблица. Третья итерация.
| 3 итерация | 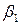 =7 =7 | 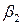 =5 =5 | 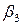 =3 =3 | 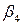 =4 =4 | 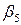 =6 =6 | наличие | ||||||||||
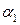 =-2 =-2 | ||||||||||||||||
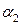 =-1 =-1 | ||||||||||||||||
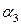 =0 =0 | ||||||||||||||||
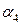 =-6 =-6 | в | в | ||||||||||||||
| -3 | -5 | -4 | ||||||||||||||
| потребность | груза |
Так как в распределительной таблице третьей итерации нет превышения потенциалов свободных клеток над потенциалами этих клеток, то в ней
представлен оптимальный план перевозок, обеспечивающий минимальные суммарные транспортные затраты. Они составят:
300  5+300
5+300  4+250
4+250  4+50
4+50  5+250
5+250  5+3
5+3  300+350
300+350  4+50
4+50  0=7500.
0=7500.
Транспортная задача решена. Составлен оптимальный план перевозок:
Оптимальный план перевозок, обеспечивающий минимум транспортных расходов.
| № п.п | поставщик 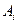 | потребитель 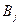 | объём перевозок 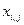 | тариф 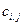 | Стоимость перевозок |
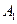 | 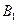 | 5*300=1500 | |||
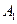 | 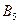 | 4*300=1200 | |||
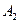 | 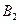 | 4*250=1000 | |||
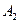 | 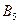 | 5*50=250 | |||
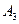 | 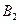 | 5*250=1250 | |||
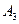 | 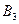 | 3*300=900 | |||
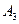 | 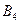 | 4*350=1400 | |||
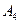 | 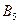 | 0*50=0 |
Общий объём поставок 1800+50. ед. Минимальная стоимость перевозок – 7500 ден. единиц.
Составим исходный опорный план методом минимального элемента. По этому методу последовательно планируется поставка потребителям максимального количества груза по минимально доступным тарифам. Часто план, составленный этим методом, бывает оптимальным.
Таблица 1 Исходный опорный план методом минимального элемента (нулевая итерация).
| 0 итерация | 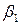 =9 =9 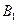 | 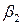 =7 =7 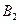 | 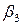 =3 =3 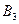 | 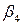 =4 =4 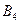 | 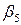 =8 =8 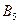 | наличие | ||||||||||
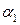 =-4 =-4 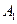 | - | 600/ | ||||||||||||||
| - | -1 | + | ||||||||||||||
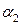 =0 =0 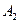 | ||||||||||||||||
| + | - | |||||||||||||||
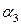 =0 =0 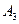 | 900/ 550/ | |||||||||||||||
| + | - | |||||||||||||||
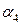 =-8 =-8 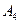 | в | в | ||||||||||||||
| -1 | -5 | -4 | ||||||||||||||
| потребность | 400/300 | груза |
Если планируется поставка груза по конкретному тарифу, этот тариф отмечаем в распределительной таблице. В центральной части клетки отмечаем планируемый объём поставки. Также отмечаем остаток груза у поставщика после запланированной поставки, или сколько груза осталась получить данному потребителю. Если какой-то тариф уже не может быть использован в дальнейшем, это также отмечаем в распределительной таблице. В табл. 2 записываем порядок составления опорного плана.
Таблица 2. Порядок составления исходного опорного плана методом минимального элемента.
| № п.п. | тариф | поставщик | потребитель | объём поставки | стоимость перевозки |
 | 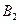 | 3*500=1500 | |||
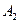 | 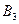 | 3*300=900 | |||
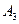 | 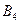 | 4*350=1400 | |||
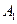 | 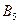 | 4*100=400 | |||
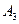 | 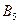 | 8*250=2000 | |||
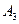 | 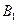 | 9*300=270 | |||
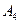 | 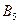 | 0*50=0 | |||
| итого |
Полученный опорный план проверяем на оптимальность методом потенциалов. Так как надо определить 9 потенциалов поставщиков и потребителей, а заполненных клеток только 7, то два потенциала можно выбрать произвольно. Вначале произвольно выбираем только потенциал 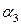 =0. Тогда
=0. Тогда 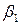 =9;
=9; 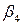 =4,
=4, 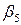 =8.
=8. 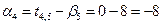 Из уравнений.
Из уравнений. 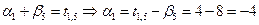 .
. 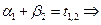
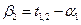 =3-(-4) = 7. Для нахождения потенциала
=3-(-4) = 7. Для нахождения потенциала 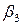 клетку
клетку 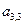 считаем заполненной с объёмом поставки
считаем заполненной с объёмом поставки 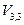 =0. Тогда:
=0. Тогда: 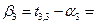 3-0=3. Из уравнения
3-0=3. Из уравнения 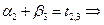
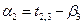 = 3-3=0. Таким образом, найдены потенциалы всех поставщиков и потребителей.
= 3-3=0. Таким образом, найдены потенциалы всех поставщиков и потребителей.
Далее находим потенциалы всех свободных клеток, отмечаем случаи превышения потенциалов над тарифами, и для свободной клетки с максимальным превышением потенциала над тарифом, составляем цикл пересчёта плана. Пересчёт плана поставок производим до получения оптимального плана
