Метод наибольшего правдоподобия

Рассмотренный выше метод моментов приводит обычно к относительно простым формулам для оценки параметров, однако в ряде случаев эти оценки малоэффективны или вовсе несостоятельны. Например, для применения метода моментов теоретические моменты должны существовать, что не для всех распределений выполняется. Например, у распределения Коши, имеющего плотность

,

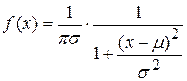все моменты бесконечны.

Поэтому необходимы и другие методы, лишенные отмеченных недостатков.

Метод наибольшего правдоподобия обладает важным достоинством: он всегда приводит к состоятельным оценкам, имеющим наибольшую точность. Этот метод наилучшим образом использует всю информацию о неизвестных параметрах распределения, имеющуюся в выборке. Однако на практике он часто приводит к необходимости решать весьма сложные системы уравнений.

Метод наибольшего правдоподобия был предложен Р.Фишером, одним из основоположников математической статистики и является наиболее обоснованным и проверенным методом, широко используемом в математической статистике.

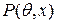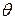Случай дискретных распределений .Рассмотрим случай оценки параметра распределения дискретной случайной величины X, вероятности значений которой определяются согласно распределению , где - неизвестный параметр, который нужно оценить по выборке .

Функция

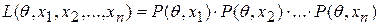
называется функцией правдоподобия. Если число случаев, когда случайная величина X приняла значения 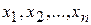равно соответственно 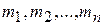, где 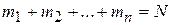- размер выборки, то функция правдоподобия

.

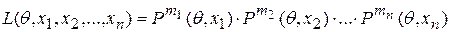Согласно методу наибольшего правдоподобия в качестве оценки неизвестного параметра 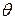принимается то значение, при котором функция правдоподобия принимает наибольшее значение для данной выборки. То есть в качестве оценки для 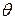берется наиболее вероятное значение для данной выборки.

Это значение находится в результате решения уравнения

.

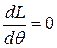Практически удобнее находить максимум функции ln(L), тогда соответствующее уравнение примет вид:

.

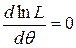Это уравнение принято называть уравнением правдоподобия. Решение этого уравнения дает максимум функции правдоподобия, если для него выполняется условие

.

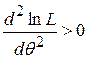Если распределение имеет два пара параметра 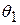и 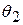, то есть имеет вид 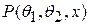, то для оценки этих параметров используются система из двух уравнений правдоподобия:

.

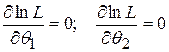При большем числе параметров число подобных уравнений соответственно увеличивается.

Проиллюстрируем применение метода наибольшего правдоподобия на примерах.

Пример 1.При n-кратном повторении опыта событие А проявилось m раз. Оценим вероятность события А по методу наибольшего правдоподобия. Будем считать, что случайная величина X принимает значение 1, если произошло событие А и 0, если произошло противоположное событие .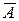

Согласно (8.1.1) функция правдоподобия в данном случае имеет вид:

,

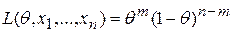где 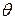- оцениваемая вероятность.

После логарифмирования получаем, что

.

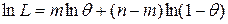После дифференцирования по 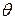получаем следующее уравнение:

,

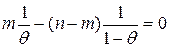после решения которого получаем, что

.

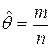Крышечкой сверху будем отличать оценку параметра от его точного значения.

Пример 2.Рассмотрим случай оценки параметра дискретной случайной величины Х, распределенной по закону Пуассона

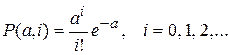
Согласно (8.1.1) функция правдоподобия равна

.

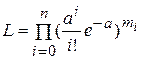После логарифмирования получаем

.

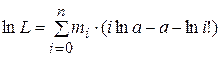После дифференцирования получаем:

,

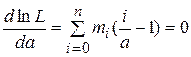Откуда

,

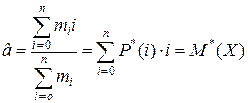где 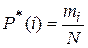- статистическая вероятность того, что X=i.

Таким образом, в качестве оценки параметра а распределения Пуассона следует брать статистическое среднее выборки.

Случай непрерывных распределений. Если случайная величина X имеет непрерывную плотность распределения 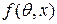, где 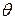- параметр распределения, который нужно оценить по выборке реализаций этой случайной величины 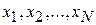, то в этом случае функция правдоподобия

.

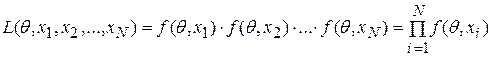Согласно методу наибольшего правдоподобия наилучшей оценкой параметра 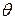является значение, для которого функция правдоподобия достигает максимума.

Если функция дифференцируема по 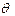, то это значение находится из уравнения

.

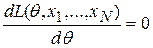Практически удобнее пользоваться логарифмической формой этого уравнения

.

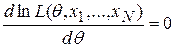Это уравнение называется уравнением правдоподобия.

Если плотность распределения случайной величины X имеет два параметра 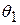и 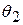, то есть имеет вид 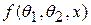, то оценки наибольшего правдоподобия находятся из системы двух уравнений

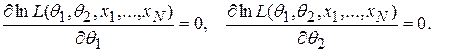
К сожалению, эти уравнения не всегда дают явные выражения для оценок параметров 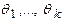и их приходится решать численными методами.

Если область определения плотности 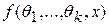зависит от параметров, то максимум функции правдоподобия может достигаться на границе этой области. В этом случае надо анализировать непосредственно функцию правдоподобия .

Если уравнение правдоподобия имеет несколько корней, то надо брать то решение, при котором функция правдоподобия максимальна.

Пример 3.Оценим данным методом параметр показательного распределения случайной величины T по выборке ее реализаций .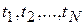

В этом случае 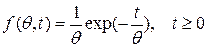, а функция правдоподобия

.

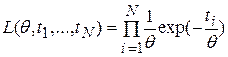Уравнение правдоподобия в этом случае имеет вид:

.

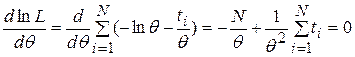В результате решения этого уравнения получаем, что оценка наибольшего правдоподобия

.

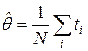Пример 4.Оценим параметры 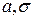случайной величины Х, распределенной по нормальному закону с плотностью

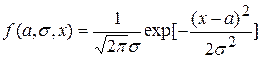
по выборке реализаций .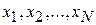

Функция правдоподобия в этом случае равна

,

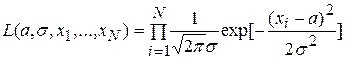а уравнения правдоподобия:

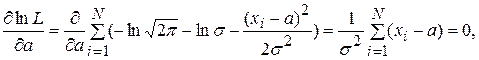
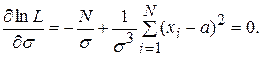
Из первого уравнения получаем, что

.

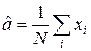Из второго уравнения получаем, что

.

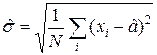В данном случае оценки наибольшего правдоподобия совпали с ранее выведенными оценками по методу моментов. Но это не всегда так.