Действующее и среднее значения переменного тока
Основной задачей расчета электрической цепи является определение тока. В цепях постоянного тока, если нет регулирующих устройств, ток остается неизменным и его легко рассчитать или измерить. В цепях переменного тока ток непрерывно меняется по величине и по направлению. Если, допустим, что каким-либо путем нам удалось определить одно мгновенное значение тока, то это не даст оценки действия всех остальных значений.
Поэтому переменный ток оценивается по его действию, которое эквивалентно действию некоторого постоянного тока. В качестве критерия такой эквивалентности принято считать тепловое действие тока.
Действующее значение переменного тока численно равно такому постоянному току, который в элементе цепи за время, равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех же условиях выделяет переменный ток.
Определим количество тепла, которое выделяется за период Т постоянным током.
По закону Джоуля – Ленца:


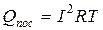 .
.
Для переменного тока
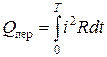 .
.
По определению количество тепла, выделяемое постоянным и переменным токами, должно быть одинаково.
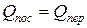 , то есть
, то есть 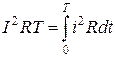 .
.
Тогда действующее значение тока определится выражением
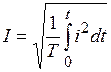 .
.
Полученное выражение справедливо для любого переменного тока независимо от его формы.
Определим действующее значение синусоидального тока. Представим мгновенное значение тока в виде 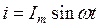 , тогда будет справедливо соотношение:
, тогда будет справедливо соотношение:
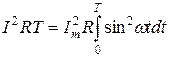 .
.
Используя правила тригонометрических преобразований, выразим
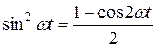 ,
,
получим
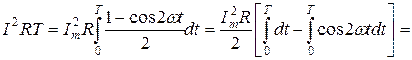
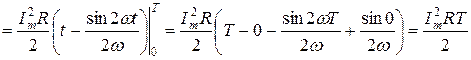 .
.
Отсюда 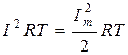 , следовательно,
, следовательно,
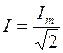 .
.
Действующее значение синусоидального тока в  раз меньше его амплитудного значения.
раз меньше его амплитудного значения.
То же самое можно сказать о напряжении и ЭДС:
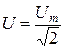 ;
; 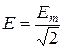 .
.
Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в цепях переменного тока выполняются для действующих значений токов, напряжений и ЭДС.
Действующее значение переменного тока можно измерить приборами любой системы, кроме магнитоэлектрической.
Отношение амплитуды к действующему значению тока называется коэффициентом амплитуды.
Для синусоидальных токов коэффициент амплитуды всегда равен  .
.
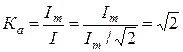 .
.
В ряде случаев при анализе электрических цепей переменного тока необходимо определить среднее значение переменного тока.
Средним значением переменного тока называется среднее арифметическое из всех мгновенных значений за половину периода.
Для синусоидальных величин среднее значение всегда оценивается за половину периода, так как мгновенные значения полпериода положительны, а полпериода – отрицательны, в результате среднее значение за период равно нулю.
Найдем среднее значение переменного тока:
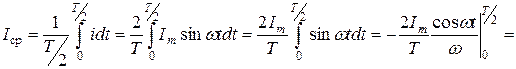
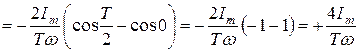 .
.
Учтем, что 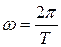 , тогда
, тогда 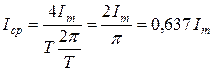 .
.
Отношение действующего значения к среднему называется коэффициентом формы кривой.
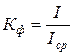 .
.
Учтем, что 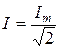 ,
, 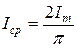 .
.
Подставив эти значения в формулу коэффициента формы, получим для синусоидального тока
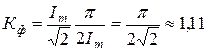 .
.
Таким образом, действующие значения тока, напряжения и э.д.с. связаны со средними значениями соотношениями:
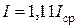 ,
, 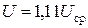 ,
, 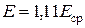 .
.
