По методу Ритца-Тимошенко

Вариационный метод Ритца-Тимошенко основан на использовании принципа возможных перемещений: упругая система находится в равновесии, если сумма элементарных работ всех внутренних и внешних сил на любом возможном перемещении равняется нулю .

Работу внешних сил (поперечной нагрузки q(X,Y)) мы обозначили через А, работу внутренних усилий через V- см.(3), поэтому математическая запись принципа возможных перемещений будет следующей [4], стр.154:

(32)

где - возможная работа нагрузки на каком-либо возможном перемещении, согласующимся с граничными условиями, а - возможная работа внутренних сил, равная с обратным знаком приращению потенциальной энергии изгиба пластины на том же возможном перемещении.

Формулу (32) приводим к виду

(33)

Выражение в скобках в (33) с обратным знаком равняется полной потенциальной энергии системы Э, поэтому (33) можно записать в виде

. (34)

Первая вариация с точностью до бесконечности малых величин высшего порядка равняется первому дифференциалу, поэтому (34) можно записать в виде

. (35)

Условие (35) означает, что потенциальная энергия системы имеет экстремальное значение. На основании теоремы Лагранжа-Дирихле [4] можно заключить, что перемещения, удовлетворяющие условиям устойчивого равновесия пластины, сообщают потенциальной энергии пластины Э минимальное значение

. (36)

Приводим формулу (36) к безразмерному виду

. (37)

Берем выражение для прогиба 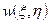в виде (5), тогда формулу (3) для и примут вид

(38)

.

Для нахождения амплитуды В прогиба 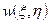, соответствующей минимуму потенциальной энергии системы, приравниваем к нулю производную

(39)

Формула (39) представляет собой линейное уравнение относительно неизвестного параметра B вида

(40)

Для нахождения параметра. В вычисляем определённые двойные интегралы, входящие в формулу (40). Проще всего сделать это следующим образом. Входящие в (40) двойные интегралы представляем в виде произведения одинарных интегралов, например:

.

Всего оказывается необходимым вычислить следующие 10 интегралов:

(41)

В качестве примера рассмотрим пластину (μ=0.3, γ=1), изображенную на рис.7.

Рис.7

Построим для нее статическим методом В.З. Власова аппроксимирующие функци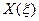и и 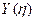имеют вид

, (42)

Нагрузка равномерно распределена по пластине, поэтому . Подставляя функции в формулы (41), вычисляем значения определенных интегралов: , , , , .

Отметим, что раньше равенства (k=1.2.3.4) получены потому, что пластина симметричная относительно диагонали, проходящей через точки ξ=1, h=0-ξ=0, h=1. В общем же случае произвольной пластины .

Подставляем вычисленные значения интервалов в формулу (34) и получаем выражение для В

. (43)

Таким образом, теперь выражение для прогиба 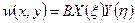полностью определено.