Экспоненциальный закон надежности

Очень часто надежность рассчитывается для периоде нормальной эксплуатации, когда l=const во времени, тогда для элемента p(t)=exp(-lt). При этом законе p(t) не зависит от сколько времени элемент проработал до рассматриваемого промежутка времени, и под временем t понимается продолжительность промежутка для которого рассчитывается надежность. Полученный закон- частный случай закона Пуассона: P_m=(a^me^-a)/m! (при m=0). Для системы содержащей К групп элементов с интенсивностями отказов l₁,l₂,…

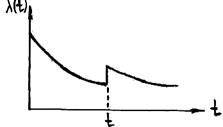P(t)=exp[-(N₁l₁+N₂l₂+...+N_kl_k)t]=exp[-tSN_il_i] (сумма от i=1 до К), где SN_il_i=L₀- интенсивность отказа системы. Это выражение позволяет ориентировочно рассчитывать значение P(t) за любой промежуток времени если известны средне групповые интенсивности отказов l_i и число элементов в группах N_i. Q(t)=1-P(t)=1-exp(-tL₀); 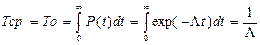, т.е. наработка на отказ и среднее время безотказной работы равны. Т.к. в период нормальной эксплуатации надежность элемента не зависит от того, сколько времени он проработал, то замена элементов должна производится только после отказа. Профилактическая замена не только не повысит надежность, но даже понизит ее, т.к. замененные элементы внесут свои приработочные отказы. Повышение надежности будет если замена элементов производится когда сказываются износовые отказы.

12. НОРМАЛЬНЫЙ ЗАКОН НАДЁЖНОСТИ

Обычно это параметрические отказы, но они так или иначе нарушают нормальную работу системы. Все элементы имеют определенный срок служб, на этот срок службы влияют многочисленные факторы следовательно результирующий закон изменения времени безотказной работы будет иметь нормальный характер, плотность распределения которого будет иметь следующий вид.

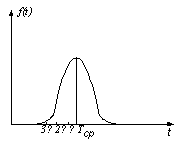При нормальном законе распределения за время t_ср отказ половины элементов. Для сравнения при экспоненциальном законе за Т_ср отказ 63% элементов.

Дифференциал нормального закона распределения времени непр. работы записывается.

f(t)=1/σ √2п*exp(-(t –Tcp)²/2σ²) ; -∞<t<∞

где Т_ср-долговечность элемента или среднее время безотказной работы; σ-среднее квадротическое отклонение σ = √_i=1∑^m(ti–Tcp)²*pi , где m- общие число значений t_i; p_{i -}вероятность того что, что случайное время работы i-го элемента будет равна t_i ; Т_ср -определенное значение max по оси времени, а значение σ определяет высоту кривой.

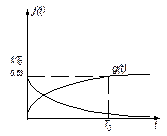Если σ₁>σ_2,то f₁(t)>f₂(t) f(t)=(1/T_o)*e^-t/To=λe^-λt;

₀∫^∞ f(t) dt =1. Эти графики представляют собой плотности времени безотказной работы . Вероятность отказа это площадь под кривой при ₀∫^t.

При нормальном распределении вероятность отказа Qп(t)=₀∫^tf(t)dt=

=(1/σ√2π)₀∫^t exp(-(t–Tcp)² /2σ²)dt

Этот интервал не берущейся, но он табулирован и приведен в справочниках. Так как значение Т_ср для всех элементов разные, то переход к нормирующему. и центрирующему. распределения U=t–T_cp/σ =>σdU = dt.

Тогда: Qп(t)=(1/√2π)₀∫^U exp(-u²/2) du=Ф(U)

Выражение это табулировано и известно под названием функциий Лапласа или Гауссовского интервала ошибок.. Функция Лапласа нечетная Ф(-u)=-Ф(u). Функция симметрична относит. Т_ср Поэтому Ф(0) = 0,5. Ф(u) = Ф0(u) +1/2

13. ПРИБЛИЖЕННЫЕ РАСЧЕТЫ НАДЕЖНОСТИ.

При проектировании желательно максимально упростить расчеты надежности. На 1 этапе расчет проводится не столько для определения критериев надежности, сколько для выбора наиболее надежного варианта. Сложность при этом заключается в том, что неизвестны интенсивности отказов всех элементов, а также условия их эксплуатации. За время, которое пройдет до изготовления могут появится более надежные элементы, поэтому расчет надежности производится в несколько этапов с последующим уточнение исходных данных т.е. числа и типа элементов и их l_i. Методы приближенного расчета:

1. По средне групповым интенсивностям отказов. Известны l_i и N_i, определить T₀ и P(t).

Порядок расчета:

а) Все элементы разбиваются на несколько групп с примерно одинаковыми интенсивностями отказов внутри групп. Подсчитывается ориентировочно количество элементов в каждой группе.

б) По таблицам находится значение l_i (либо среднее, либо крайнее минимальное или максимальное значение).

в) Вычисляется произведение N_il_i.

г) Рассчитывается общая L₀ системы L₀=SN_il_i(сумма от i=1 до К).

д) Определяется наработка на отказ T₀=1/L₀.

е) Определяется вероятность безотказной работы P(t)=exp(-t/T₀)

Недостаток метода- ограниченность применения, т.к. не всегда известны значения l_i в проектируемой системе.

2. С использованием данных из опыта эксплуатации.

При ориентировочном расчете надежности проектируемой аппаратуры иногда используют данные о надежности аналогичной по типу и назначению аппаратуры, которая уже разработана и используется. Условия при расчете: 1) используются однотипные элементы с одинаковыми l_i; 2) соотношение N_i/N у системы аналога и проектируемой системы должно быть одинаково; 3) примерно одинаковые режимы работы и схемные решения. В основе метода лежит предположение о том, что l_ср в проектируемой системе и в системе аналоге равны: l_ср=1/(N_aT_0a)=1/(N_пT_0п). Зная N_a и T_0a аппаратуры аналога определятся наработка на отказ проектируемой аппаратуры: Т_0п=(N_aT_0a)/N_п. Достоинства- простота, недостаток- ограниченность применения т.к. аналогов не много.

3. По интенсивностям отказов элементов.

Заключается в том, что рассчитанные по таблицам значения l_i проектируемой системы приводятся к реальным условиям эксплуатации посредством коэффициента пересчета. Исходные данные: l_i- всех элементов (по справочнику и паспорту) как для аналога так и для проектируемой системы; N_ai и N_пi- количество элементов в группах; T_0a- по результатам эксплуатации. Порядок расчета:

а) определяется расчетная наработка на отказ T_0pa=1/SNa_il_i(сумма от 1 до К, где К- число групп);

б) из статистических данных берется фактическое T_0a аналога и определяется коэффициент пересчета h= T_0a/T_0pa;

в) рассчитывается T_0pп=1/SNп_il_i(сумма от 1 до К, где К- число групп в проектируемой системе);

г) определяется T_0п=hT_0pп с учетом условий эксплуатации.

14. ОКОНЧАТЕЛЬНЫЙ РАСЧЕТ НАДЕЖНОСТИ.

Производится для готового проекта. По схемам определяют температуру и нагрузку на каждый элемент системы. Сущность расчета- вместо средне групповых интенсивностях отказов элементов l_i в формулы подставляем l_i(n), зависящее от режимов работы и температуры. Значения l_i(n) определяется по формулам, таблицам или графикам. При этом предполагается, что справедлив экспоненциальный закон распределения и отказы элементов взаимно не зависимы. Для расчета необходимо знать : 1) режимы работы каждого элемента (коэфф. нагрузки Кн, температуру); 2) количество элементов одного типа с одинаковым режимом работы N_i; 3) l_i элементов в соответствующих режимах т.е. l_i(n). Расчет ведется по тем же формулам что и приближенный расчет: L(n)=SN_il_i(n) (сумма от 1 до к); T(n)=1/L(n); P(t)=exp[-tL(n)]=exp[-1/T₀(n).

Расчет надежности удобно производить поэтапно:

а) разделяют аппаратуру на блоки, узлы и каскады и строится структурная схема расчета надежности;

б) в каждом блоке проводится анализ элементов и температурного режима и определяется коэффициент нагрузки элементов Кн и температуры;

в) определяется l_i(n) при заданных режимах;

г) определяется интенсивность отказа блока Lбл.;

д) определяется общая интенсивность отказа системы Lсис.=SL_i(n)( сумма от 1 до m, где m- количество блоков) и остальные характеристики надежности.

Опыты эксплуатации аппаратуры показывают, что при высокой частоте включения и выключения аппаратуры происходит увеличение l_i. Интенсивность отказов такого устройства l(n)=l_раб(n)+nl_ц, где l_раб(n)- интенсивность отказов устройства в рабочем состоянии; l_ц- интенсивность отказов за один цикл включения; n- частота включения в течении одного часа.

Если при определении характеристик надежности в интервале времени t окажется, что часть этого времени система находилась в выключенном состоянии (t_хран=t-t_раб), то учитывают что в выключенном состоянии l_сис=l_хран меньше l_раб(n). Учитывая работу, хранение и включение аппаратуры вероятность безотказной работы 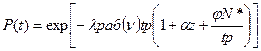, где a=l_хран/l_раб; z=t_хран/t_раб; j=l_ц/l_р(n); l_хран=(0,1¸0,01)l_р(n); N*- общее время включения за время t.

15. НАРАБОТКА НА ОТКАЗ Т₀. ГАММА-ПРОЦЕНТНАЯ НАРАБОТКА НА ОТКАЗ

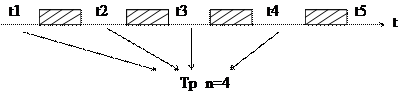Под этим термином понимают среднее число часов работы между двумя отказами (соседними). Т₀*=Т_р/n, где Т_р- время исправной работы (суммарное) за рассматриваемый промежуток времени t; n- число отказов за время t. Графически процесс определения времени Т_р можно показать следующим образом:

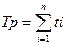
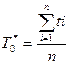С целью ускорения испытаний и получения более точных результатов наработка на отказ может определятся по ряду одинаковой аппаратуры: 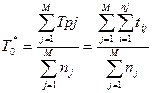, где М- число комплектов испытуемой аппаратуры; Tpj- суммарное время исправной работы j-го комплекта; n_j- число отказов в j-том комплекте. Если l=const и f_ср(t)=const, то 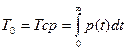. Он учитывает реальные условия эксплуатации. Недостаток: не видно изменения надежности во времени.

Гамма – процентная наработка на отказ

ν = е ^-(t/T0) За время t вероятность безотказной работы T0