Проверка статистических гипотез и критериев

Смысл проверки статистических гипотез состоит в том, чтобы по данным случайной выборки принять наиболее обоснованное решение о виде или параметрах генеральной совокупности, т.е. принять или отклонить гипотезу с минимальным риском ошибки.

Основной принцип проверки статистических гипотез: если наблюдаемое (расчётное) значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое (расчётное) значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают [5].

Гипотезы и критическую область следует определять до проведения выборки. Строгое решение этой задачи достигается при помощи метода отношения правдоподобия [14].

С помощью критериев проверки статистических гипотез решаются задачи:

– проверка гипотез об основных параметрах генеральной совокупности (средняя, дисперсии и др.);

– проверка гипотез о распределениях;

– проверка существенности связи между параметрами и др.

Проверка статистических гипотез производится в таком порядке:

1. Формулируются гипотезы H₀ и H₁.

2. Выбирается уровень значимости a.

3. Определяется соответствующая уровню значимости критическая область.

4. Проводятся измерения выборки.

5. По результатам выборки рассчитывается фактическое значение статистической характеристики.

6. Принимается или отвергается нулевая гипотеза.

Далее рассмотрим комплексы, которые используются при обработке результатов экспериментов и которые носят название критериев.

Критерий Пирсона — c² — служит для проверки согласия экспериментального и теоретического распределений.

Критерий Фишера, или F-критерий, используется для сравнения двух выборочных дисперсий, определённых по независимым выборкам из нормальных генеральных совокупностей.

Проверяется гипотеза H₀: D(X) = D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H₁: D(X) > D(Y).

Используется критерий (статистика) Фишера, который представляет отношение большей выборочной дисперсии к меньшей:

.

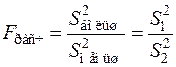По таблице критерия Фишера при числе степеней свободы k₁ = n₁ – 1 и k₂ = n₂ – 1 и выбранном уровне значимости a определяют F_кр (a; k₁; k₂). Здесь n₁ и n₂ — объёмы выборок.

Если конкурирующая гипотеза H₁: D(X) ¹ D(Y), то критическую точку ищут при уровне значимости 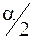(вдвое меньше заданного): F_кр ( 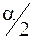; k₁; k₂).

Если F_расч < F_кр, то нет оснований отвергать нулевую гипотезу о равенстве дисперсий.

При применении F-критерия полагают, что все наблюдения независимы и распределены нормально с одинаковыми математическими ожиданиями и одинаковой дисперсией. Однако исследования показывают, что F-критерий применим, когда распределение отличается от нормального. При этом наиболее существенное влияние на результат оказывает эксцесс распределения Е, а не асимметрия. Следовательно, асимметричность распределений не является препятствием для применения F-критерия. Однако следует осторожно относиться к распределениям, эксцесс которых значительно отличается от трёх (Е = 3 для нормального распределения).

Критерий Стьюдента, или t-критерий, используется для проверки гипотезы о равенстве двух средних значений генеральных совокупностей, имеющих нормальные законы распределения, через выборочные средние значения случайной величины. Расчётные значения t_расч получают по соответствующим формулам, применение которых зависит от того, известны дисперсии генеральных совокупностей или нет, и от объёма выборок [5].

Если дисперсии неизвестны и одинаковы (малые независимые выборки), то расчётное значение критерия определяется по формуле

,

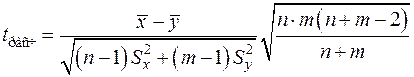где n и m — объёмы малых независимых выборок; и — выборочные средние; 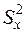и — исправленные выборочные дисперсии.

Выборки считаются малыми, если n < 30 и m < 30.

По таблице критерия Стьюдента при числе степеней свободы k = n + m – 2 находят t_{двуст. кр} (a;k). Прежде чем сравнивать средние, необходимо проверить, существует ли разница между средними квадратическими ошибками обеих сери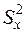й и . Если F-критерий даёт значимое различие между ними, т.е. нулевая гипотеза H₀: 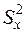= отвергается, то исследуемые два средних значения нельзя сравнивать между собой.

Исправленные выборочные дисперсии находят через условные варианты по формуле

,

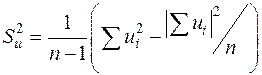где u_i — условные варианты для x_i.

Аналогично: v_i — условные варианты для y_i.

Условные варианты — это преобразованные реальные варианты x_i и y_i. Такое преобразование проводится с целью упрощения расчётов и записей исследуемых величин, так как условные варианты представляют собой только целые числа.

Например: x_i = 3,4; = 3,6; составляем формулу для вычисления условного варианта

u_i = 10x_i – 36 = 10 × 3,4 – 36 = – 2.

Если дисперсии неизвестны и выборки зависимые и одинакового объёма, то расчётные значения критерия определяются по формуле

,

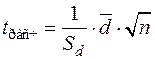где 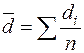— средняя разностей вариантов;

d_i = x_i – y_i — разность вариантов с одинаковыми номерами;

n — объём одной выборки;

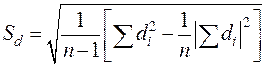— исправленное среднее квадратическое отклонение.

По таблице критерия Стьюдента при числе степеней свободы k = n - 1 и выбранному уровню значимости для двусторонней критической области (т.к. нулевая гипотеза 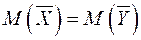) находим критическую точку t_{двуст. кр} (a;k).

При сравнении выборочной средней с гипотетической генеральной средней нормальной совокупности необходимо выполнение одного из условий: дисперсия генеральной совокупности известна или нет.

Если дисперсия генеральной совокупности неизвестна, то используют критерий Стьюдента, расчётное значение которого определяют по формуле

,

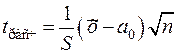где — выборочная средняя;

a₀ — гипотетическая средняя генеральной совокупности;

n — объём выборки (малая выборка);

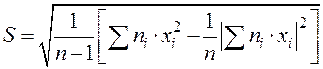— исправленное среднее квадратическое отклонение.

По таблице критерия Стьюдента при числе степеней свободы k = n – 1 определяем t_{двуст. кр} (a;k). Во всех случаях принимается нулевая гипотеза, если t_расч < t_крит.

Если сравниваются средние двух генеральных совокупностей с известными дисперсиями и большими независимыми выборками, а также если сравнивается выборочная средняя с гипотетической средней генеральной нормальной совокупности с известной дисперсией, то для сравнения используются другие критерии (не критерии Стьюдента), которые определяются по таблице функции Лапласа [5].

Критерий Кохрена (Кохрана, Кочрена), или G-критерий, используется для проверки однородности (равенства) нескольких (> 2) дисперсий, определённых по выборкам одинакового объёма. Проверяется нулевая гипотеза о равенстве между собой генеральных дисперсий:

.

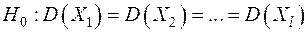В качестве критерия используется отношение максимальной выборочной дисперсии 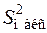к сумме всех выборочных дисперсий

.

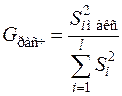По числу степеней свободы k = n – 1 и количеству выборок l при выбранном уровне значимости a по таблице критерия Кохрена определяют G_кр (a; k; l). Если G_расч < G_кр, то нет оснований отвергать нулевую гипотезу об однородности выборок. Для проверки нулевой гипотезы строят правостороннюю критическую область. Если сравниваются несколько дисперсий нормальных генеральных совокупностей по выборкам разного объёма, то используется критерий Бартлетта [5].

1.10 Выбор информативных параметров эксперимента [6]

1. Характеристика объекта исследования

Под объектом следует понимать систему, которая подлежит изучению или оптимизации. Основным свойством объекта исследования является его сложность, определяемая числом различных состояний, в которых может находиться объект.

Важной характеристикой объекта исследования является его управляемость. Управляемым считается объект, который экспериментатор по своему усмотрению может перевести в любое из различных состояний и поддерживать его в этом состоянии с заданной точностью заданное время. Свойство управляемости объекта позволяет проводить на нём «активный» эксперимент, который заключается в непосредственном воздействии на объект по воле экспериментатора.

Промышленные объекты в большинстве случаев не позволяют проводить на них активные эксперименты. В такой ситуации проводятся пассивное наблюдение за объектом и фиксация интересующих параметров без непосредственного воздействия, т.е. осуществляется «пассивный» эксперимент.

Задача изучения объекта исследования в значительной мере облегчается его формализацией или удачным выбором его модели. Это зависит также от объёма эксперимента, который, в свою очередь, определяется количеством параметров оптимизации (выходных параметров) и количеством факторов, влияющих на объект. Следовательно, для обеспечения эффективного эксперимента необходимо правильно выбрать и количество выходных параметров, и количество исследуемых факторов.

2. Выбор параметра оптимизации

В соответствии с базовыми положениями системного подхода одним из главных требований к системе является её оптимальное функционирование в заданных условиях эксплуатации. Поэтому выбор параметров оптимизации является наиболее важным моментом при подготовке экспериментальных исследований.

Один из принципов системного подхода в области оптимального проектирования состоит в том, что система должна оптимизироваться по единственному и количественно определённому критерию (показателю), отражающему в математической форме цель оптимизации. Этим показателем является целевая функция, которая устанавливает связь между входными (факторами) и выходными параметрами системы. Однако обычно реакция системы на возмущающие воздействия (желательные и нежелательные) многогранна, и поэтому в большинстве случаев приходится решать задачи с несколькими параметрами оптимизации. Эти параметры, естественно, могут быть разнообразными. Условно их можно разделить:

– на технические (мощность, чувствительность, быстродействие и др.);

– технико-экономические (производительность и др.);

– экономические (экономическая эффективность функционирования, рентабельность и др.);

– технологические (показатели качества продукции);

– статистические (математическое ожидание и дисперсия точности, стабильности и т.п.).

Основные требования, предъявляемые к параметру оптимизации, следующие: однозначно, эффективно и достаточно универсально характеризовать объект исследования.

Требование однозначности в статистическом смысле заключается в том, что определённому набору значений факторов должно соответствовать только одно (с точностью ошибки эксперимента) значение параметра оптимизации.

Планирование считается эффективным, если выбран параметр оптимизации, который можно определить с наибольшей возможной точностью.

Под универсальностью параметра оптимизации подразумевается его способность всесторонне характеризовать объект.

Желательно, чтобы параметр оптимизации имел чёткий физический смысл, был понятен исследователю и легко измеряем.

Существенную роль при выборе параметра оптимизации играет уровень априорных сведений об объекте исследования.

При возникновении ситуации с несколькими параметрами оптимизации прежде всего необходимо рассмотреть возможность уменьшения их числа, в лучшем случае до одного. Это возможно следующими путями:

– прежде всего, надо переформулировать задачу, пытаясь изменить параметры оптимизации;

– в сложных случаях можно расчленить задачу на ряд более мелких и решать их последовательно так, чтобы на каждом шаге оптимизация проводилась только по одной целевой функции (ранжированная форма целевой функции). При этом необходимо следить за тем, чтобы цели исходной и расчленённой задач соответствовали друг другу;

– уменьшить число параметров оптимизации можно путём оценки корреляции между ними. Задача сводится к определению коэффициентов парной корреляции на основе экспериментальных материалов и статистической оценки их значимости. При высокой значимости коэффициента корреляции исключается один из двух рассматриваемых параметров, так как он не несёт полезной информации по отношению к другому. Обычно исключается тот параметр оптимизации, который труднее измерить;

– уменьшить количество параметров оптимизации можно нахождением обобщённого параметра (аддитивного, мультипликативного, минимаксного).

Необходимо заметить, что выбор параметра оптимизации в значительной степени влияет на вид математической модели, которая получается в результате исследования объекта.

3. Выбор исследуемых факторов

После выбора параметра оптимизации приступают к выбору способов воздействия на объект исследования, т.е. факторов — независимых переменных, входных величин, обладающих свойством воздействовать на этот объект. Лучше всего, если будут выбраны все возможные факторы. Чем больше, тем лучше. Но включить в эксперимент все известные факторы не представляется возможным, так как это значительно увеличит объём эксперимента. Поэтому отбирают факторы, оказывающие наиболее существенное влияние на объект исследования. При выборе факторов необходимо учитывать требования, которые к ним предъявляются:

1. Лёгкость измерения с достаточно высокой точностью.

2. Однозначность.

3. Управляемость.

4. Совместимость друг с другом.

5. Отсутствие корреляционных связей между ними.

Все факторы можно разделить на качественные и количественные. Качественные факторы те, которые не могут быть представлены в количественном виде. Например, марка материала, тип станка, вид экспериментальной установки и т.п. Количественные факторы те, которые можно оценивать количественно, т.е. измерять.

Желательно оперировать с однозначными факторами, которые непосредственно воздействуют на объект исследования. Значительно труднее работать со сложными факторами, являющимися функциями других факторов.

Требование управляемости факторов заключается в возможности выбора и поддержания уровня варьирования фактора в течение всего опыта, что позволяет активно воздействовать на объект исследования. Появление неуправляемых факторов является результатом наличия различного вида неоднородностей дискретного и непрерывного типа. Источником неоднородностей дискретного типа могут быть различные свойства обрабатываемых материалов, измерительной аппаратуры, квалификация исполнителей и т.п. Существенным источником неоднородностей может служить так называемый «эффект рук», связанный с получением результатов различными исполнителями. Источники неоднородностей, как правило, являются факторами, которые мало интересуют исследователя. Они в значительной степени увеличивают ошибку эксперимента, создают большое «шумовое» поле. Влияние неоднородностей более желательно устранить, чем оценить.

Источники неоднородностей непрерывного типа вызывают непрерывные изменения исследуемых факторов и, как результат, дрейф параметра оптимизации во времени. Например, изменение во времени температуры оборудования, старение оборудования и т.п.

Необходимо стремиться учесть и оценить влияние как можно большего числа неуправляемых контролируемых факторов. Неконтролируемые неуправляемые факторы являются неизмеряемыми, что значительно увеличивает ошибку эксперимента.

Особенно важным является требование совместимости факторов, которое заключается в том, что все комбинации уровней факторов, участвующих в эксперименте, могут быть осуществлены на практике и являются безопасными. Несовместимость факторов возникает тогда, когда некоторые из комбинаций их значений не могут быть осуществлены. Например, некоторое сочетание скорости резания, подачи и глубины резания приводит к возникновению интенсивных вибраций и работа станка невозможна.

Требование независимости заключается в возможности установления фактора на любом уровне вне зависимостей от уровней других факторов. То есть необходимо, чтобы отсутствовала корреляция факторов. Включение в эксперимент коррелированных факторов не способствует получению новых результатов, так как один из факторов не несёт никакой дополнительной информации об объекте исследования.

Требование некоррелированности, однако, не исключает возможности наличия связей любого характера. Достаточно, чтобы эта связь не была линейной.

Выбор факторов с учётом указанных требований завершается составлением полного списка факторов. В список включаются те факторы, которые целесообразно и удобно варьировать в ходе эксперимента; для остальных назначаются постоянные уровни. Если число факторов превышает 10 — 12, то решается вопрос о проведении отсеивающих экспериментов.

1.11 Метод экспертных оценок для отбора факторов [7]

Для уменьшения объёма эксперимента при большом количестве факторов естественно возникает желание отсеять малозначимые факторы. Для этого следует надёжно провести отбор факторов. Но это можно сделать лишь на основе экспериментальных данных, которых на этапе построения математической модели, как правило, ещё недостаточно. Выход состоит в тщательном анализе косвенных данных и привлечении мнений экспертов. Метод отбора существенных факторов на основе анализа мнений специалистов-экспертов называется методом экспертных оценок. Надёжность этого метода не очень высока. Поэтому даже на начальном этапе требуется проверка согласованности мнений специалистов. Для этого используется метод ранговой корреляции.

Рассмотрим метод экспертных оценок. Пусть число факторов, которые следует учесть при построении модели, равно m. На основе литературных данных и мнений специалистов каждому фактору приписывается некоторый ранг. Наиболее важному фактору, с точки зрения специалиста, приписывается ранг m, следующему по важности фактору приписывается ранг (m – 1)и т.д. Наименее важный фактор имеет ранг единицу. Если несколько факторов имеют одинаковую важность, то им приписывается одинаковый ранг, который равен среднему арифметическому рангов, приходящихся на эту группу факторов. Данные о рангах факторов заносятся в сводную таблицу мнений специалистов.

Таблица 1.1

Фактор	Специалисты	Сумма рангов
		…	k
x1	a11	a12	...	a1k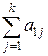
x2	a21	a22	...	a2k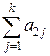
. . .	. . .	. . .	. . .	. . .	. . .
xm	am1	am2	...	amk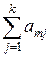

Мнения отдельных специалистов о рангах разных факторов, безусловно, расходятся. Поэтому для каждого фактора суммируют его ранги у разных специалистов и получают сумму рангов по каждому фактору. Затем строят диаграмму суммы рангов факторов (рис. 1.4).

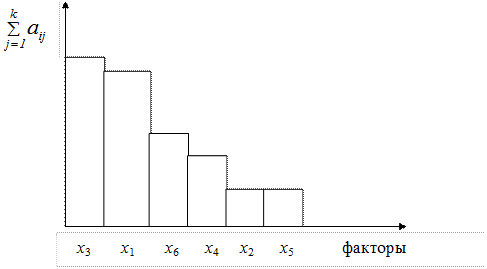
Рисунок 1.4 — Диаграмма рангов факторов

Анализ диаграммы показывает, что, например, из 6 факторов наибольшее значение имеют факторы x₃ и x₁, существенно меньшее — x₆ и x₄ и малое значение специалисты придают факторам x₂ и x₅. Поэтому в первом приближении можно пренебречь факторами x₂ и x₅.

Чтобы оценить степень согласованности мнений экспертов относительно рангов факторов, вычисляют коэффициент ранговой корреляции, который носит название коэффициента конкордации W (от лат. concordare — быть согласным), или коэффициента согласованности.

Этот коэффициент лежит в пределах от 0 до 1. Если при ранжировании факторов согласие мнений экспертов полностью отсутствует, то W = 0. Если имеет место полное согласие мнений экспертов, то W = 1.

Вычисляют коэффициент конкордации по следующей схеме.

1. Находят среднее арифметическое суммы всех рангов

.

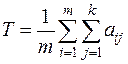2. Находят отклонение суммы рангов каждого фактора от среднего арифметического

.

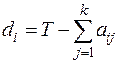3. Находят сумму квадратов отклонений d_i

.

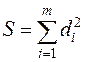Величина S, очевидно, есть некоторая характеристика согласия мнений экспертов. Если согласия нет, то при большом k все d_i » 0 и S = 0. При полном согласии мнений экспертов S = S_макс.

Коэффициент конкордации определяется по формуле

, .

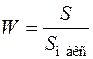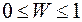Расчёт S_макс проводится в зависимости от того, имеет каждый фактор отличный от других ранг или имеются группы факторов с одинаковыми рангами каждого фактора.

Рассмотрим случай, когда все факторы имеют разные ранги. При этом используют формулу

.

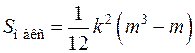Тогда коэффициент конкордации будет равен

.

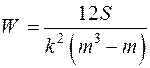Оценку значимости коэффициента конкордации обычно проводят по c²-критерию, который вычисляют по формуле

.

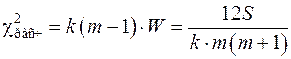Полученное значение сравнивают с табличным значением 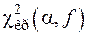, где a — уровень значимости, f = m – 1 — число степеней свободы. Если 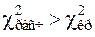, то величина W считается значимой и, следовательно, мнения экспертов согласуются. Если 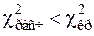, то на уровне значимости aсогласие мнений экспертов отсутствует. Если коэффициент конкордации значим, то построенной диаграмме можно верить. На диаграмме следует выделить группу факторов, наиболее сильно влияющих на параметр оптимизации y. Слабо влияющие факторы на первом этапе исследования можно исключить из рассмотрения, хотя такой подход тоже будет субъективным.

По результатам анализа диаграммы принимают следующие решения. Если распределение на диаграмме суммы рангов равномерное, то все факторы должны включаться в эксперимент. Значит, опрос мнений экспертов не дал положительного результата. Если распределение неравномерное, но отличие рангов незначительное, то различие между факторами делается неуверенно. Поэтому в этом случае также лучше все факторы включить в эксперимент. Наиболее благоприятный случай, когда происходит быстрое экспоненциальное уменьшение степени влияния факторов, что даёт возможность более уверенно отсеять ряд факторов на основе проведённого опроса мнений экспертов. На практике применяют и ряд других методов отсеивания факторов.

Разложение вариации

При проведении экспериментов приходится оценивать, например, влияние того или иного фактора на результаты процесса или насколько близка вычисленная функция к эмпирическим данным. Такая оценка основана на правиле разложения вариации. Для этого общая сумма квадратов отклонений результативного признака SS_общ делится на две суммы: сумму квадратов отклонений, связанную с влиянием данного фактора SS₁, и сумму квадратов отклонений, связанную с действием неучтённых факторов SS₂:

SS_общ= SS₁+ SS₂.

Эти суммы, деленные каждая на соответствующее ей число степеней свободы, дают соответствующие дисперсии.

Вопросы для самопроверки

1. Какие два подхода используются для изучения объектов?

2. Определите понятие эксперимента.

3. Что лежит в основе эксперимента?

4. Из каких этапов состоит проведение эксперимента и по каким направлениям развивается теория эксперимента?

5. Что такое вычислительный эксперимент?

6. Какие разделы входят в теорию статистических выводов и какие методы применяются для решения их задач?

7. Какие существуют методы многомерного анализа?

8. Какие существуют типы экспериментов и в чём они состоят?

9. Какие факторы влияют на точность модели?

10. Какие могут быть ошибки при принятии решения по результатам эксперимента (испытаний)?

11. Определите понятия: статистическая, нулевая и альтернативная гипотезы.

12. Какие критерии используются для проверки гипотез?

13. Какие основные требования предъявляются к параметру оптимизации?

14. Какие выбирают исследуемые факторы и какие к ним предъявляются требования?

15. В чем состоит метод экспертных оценок?

16. В чем состоит разложение вариации?