Сандық интегралдау есебінің қойылуы

Келесідей анықталған интегралды есептегенде

,

мұндағы функциясы кесіндісінде үздіксіз, кейде белгілі Ньютон – Лейбниц формуласын қолдануға болады:

(1)

мұндағы функциясының алғашқыбейнелерінің бірі болады (яғни, ). Бірақ, сирек жағдайда, тәжірибе жүзінде алғашқыбейнені аналитикалық түрде алғанның өзінде, анықталған интегралдың сандық мәнін нақты соңына дейін есептей алмаймыз. Оған қоса, кейде интеграл астындағы функция таблица немесе график түрінде берілсе, онда интегралды не үшін (6.18) формуласымен есептеу кең ауқымды практикалық қолданыс алмайтыны түсінікті болар еді.

Мұндай жағдайда жуықтап (сандық) интегралдаудың әртүрлі тәсілдері қолданылады.

Бір еселі интегралдарды жуықтап есептеуге қолданылатын формулалар квадратуралық формулалар деп аталынады. Квадратуралық формулаларды құрудың қарапайым әдісі мынадай болады. Интеграл астындағы функциясы кесіндісінде интерполяциялау көпмүшелігімен алмастырылады. Мысалы, -Лагранж көпмүшелігімен алмастырсақ, мынадай жуықтау теңдігі құрылады:

, (2)

Мұндай әдіс ЭЕМ-де жеңіл орындалатын алгоритмдерге әкеліп, нәтижені нақты алу мүмкіндігін береді. Бұл жағдайда, кесіндісі 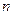бөлікке нүктелерімен бөлінеді, соның нәтижесінде көпмүшелігі құрылады.

Алынған нәтижені көпмүшелігінің орнына қоя отырып, біз

,

мәнін аламыз.

Сонымен

, (3)

мұндағы

, (4)

Осы табылған формулалар нәтижесін біле отырып, мынаны байқауға болады:

1). коэффициенттері функциясына тәуелді еместігі, себебі олар интерполяциялау түйіндерін ескеріп құрылған.

2). Егер , 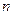-ші дәрежелі полином болса, онда (2) формуласы нақты болады, себебі, бұл жағдайда .

Мұндағы x_к-интерполяцияның берiлген түйіндер, А_к-функцияның түрiне тәуелді емес тек түйіндер таңдауына тәуелдi коэффициенттер, R-қалдық мүше немесе квадратуралық формуланың қателiгi.

интегралдау кесiндiсiн тең n бөлiкке бөлемiз:

интеграл астындағы функцияны алынған тораптарда есептеймiз.

Бiрдей қашықтықта жатқан тораптар үшiн квадратуралық формулалар Ньютон-Котес формулалары деп аталады. Бұндай формулалардың қарапайым түрлерi төменде келтiрiлген:

11.2 Трапеция формуласы.

(5)

мұндағы .

Қалдық мүшесi келесi түрде есептелiнедi:

11.3. Симпсон формуласы.

,

(6)

Қалдық мүшесi келесi түрде есептелiнедi:

11.4. Ньютон формуласы.

(7)

мұндағы

.

Қалдық мүше келесi түрде есептелiнедi:

МЫСАЛ.

Келесі интегралды Симпсон формуласымен n=10 болғанда есептеу керек:

Шешуі.

Қалдық мүшені бағалау үшін функцияның төртінші ретті туындысын табайық.

y⁽⁴⁾(x) туындысы [0, 1] кесіндісінде x=1 болғанда ең үлкен мәнді қабылдайды. Сондықтан

|R₂|£

функциясының мәндер кестесін құрайық.

i	x
	0,0	0,00	1,0000   2,7188 3,7188
	0,1	0,01		1,0101
	0,2	0,04	1,0408
	0,3	0,09		1,0942
	0,4	0,16	1,1735
	0,5	0,25		1,2840
	0,6	0,36	1,4333
	0,7	0,49		1,6323
	0,8	0,64	1,8965
	0,9	0,81		2,2479
	1,0	1,00
Қосынды	5,5441	7,2685

Симпсон формуласымен интегралды есептеп,

,

нәтижені төрт таңбаға дейін дөңгелектейміз: