Фундаментальная система решений однородной системы линейных уравнений
Определение. Фундаментальной системой решений однородной системы линейных уравнений (ФСР ОСЛУ) называется система решений, которая удовлетворяет следующим условиям:
1) является линейно независимой;
2) каждое решение данной системы линейных уравнений линейно выражается через эту систему решений.
Теорема.ФСР ОСЛУ содержит n-r решений, где n - число неизвестных, r – ранг основной матрицы системы.
Прежде чем доказать теорему, рассмотрим следующий пример.
Пример.
Найти ФСР ОСЛУ:
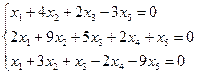
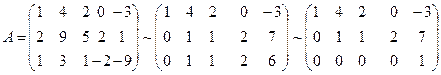
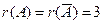
ФСР состоит из n-r= 5-3=2 векторов.
Пусть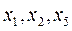 
- главные неизвестные, 
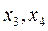- свободные неизвестные.
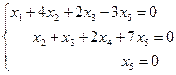
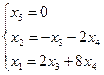
Общее решение системы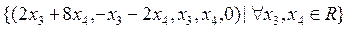 
.
По-другому: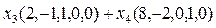 
.
.
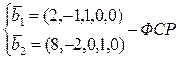Доказательство теоремы
Рассмотрим систему линейных уравнений
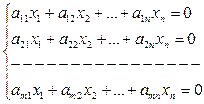 | (2.6) |
I. Обозначим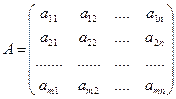 
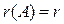- ранг матрицы; n – число неизвестных.
Пусть первые r строк и первые r столбцов линейно независимы.
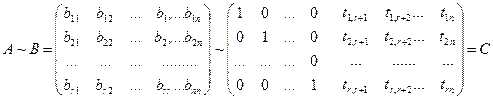
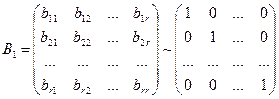
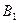- неособенная и может быть приведена к единичной с помощью элементарных строчечных преобразований.
Однородная система линейных уравнений, соответствующая матрице С
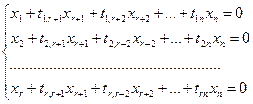 | (2.6') |
равносильна исходной системе линейных уравнений.
Пусть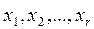 
- главные неизвестные; 
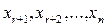- свободные неизвестные.
II. Придавая свободным неизвестным произвольные значения, вычислим соответствующие значения главных неизвестных.
В частности,
, 
,…, 
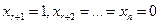
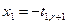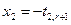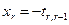
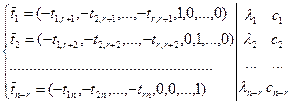 | (2.7). |
Покажем, что система (2.7) является фундаментальной системой решений однородной системы линейных уравнений системы (2), а следовательно и исходной системы.
III. Покажем, что система (2.7) является линейно независимой.
Рассмотрим равенство:
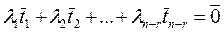(2.8)
Выполнив в левой части этого равенства операции умножения на скаляр и сложения векторов, получим:
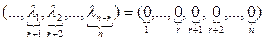
Из этого равенства видно, что по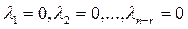 
Равенство (2.8) выполняется при нулевом наборе скаляров, следовательно (2.7) – линейно независима.
IV. Покажем, что каждое решение ОСЛУ линейно выражается через систему (2.7).
Пусть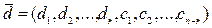 
- какое-либо решение системы (2.6). Тогда
=
= 
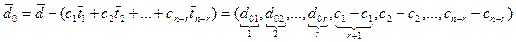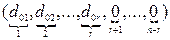= из системы (2.6') получаем =
= 
, 
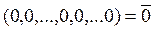
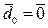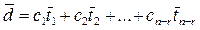
Так как получили, что любое решение системы линейных уравнений линейно выражается через систему (2.7), доказательство теоремы завершено.
Упражнения
11. Решить системы уравнений методом Гаусса
a)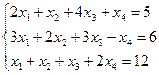 
;
b)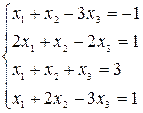 
;
c)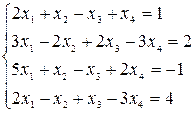 
;
d)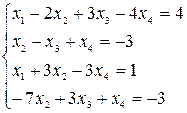 
;
e)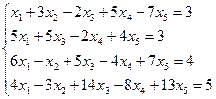 
.
12. Исследовать методом Гаусса системы с параметром
a)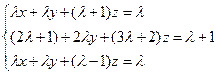 
;
b)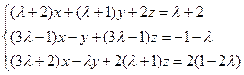 
;
c)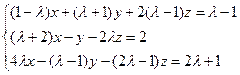 
;
d)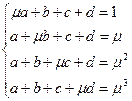 
.
13. При каких значениях параметра m система имеет единственное решение?
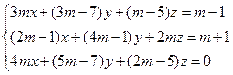
14. Найти общее решение и ФСР ОСЛУ
a)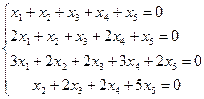 
;
b)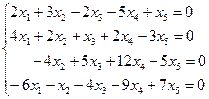 
;
c)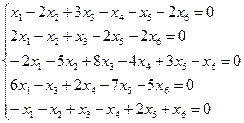 
.
15. Подобрать параметр так, чтобы система уравнений имела решение
a)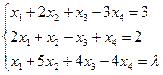 
;
b)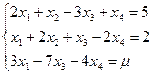 
;
c)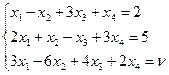 
.
16. Дана конечная система векторов:
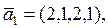
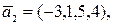
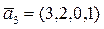
Найти
a)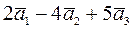 
;
b)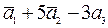 
;
c)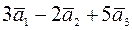 
.
17. Дана система векторов: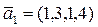 
, 
, 
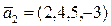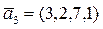Найти:
a)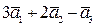 
;
b)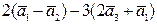 
;
c)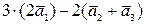 
.
18. Является ли линейно зависимой следующая система векторов?
a)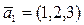 
, 
, 
;
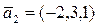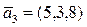b)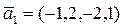 
, 
;
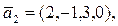
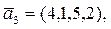
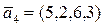c)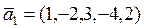 
, 
, 
, 
.
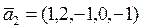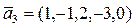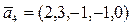19. Показать, что данная система векторов является линейно независимой:
a)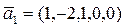 
, 
, 
;
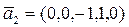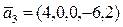b)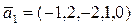 
, 
, 
;
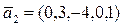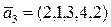c)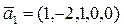 
, 
, 
.
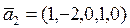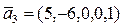20. Выяснить, является ли следующая система векторов линейно зависимой. Найти ее базис и ранг.
a)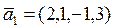 
, 
, 
, 
, 
;
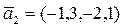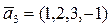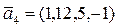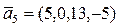b)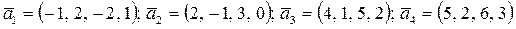 
;
c)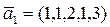 
, 
, 
, 
.
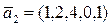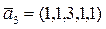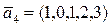21. Доказать, что если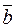 
можно единственным образом выразить как линейную комбинацию 
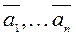, то 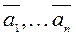- линейно независимая система.
22. Найти ранги матриц:
a)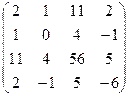 
;
b)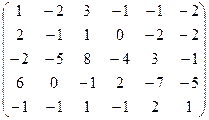 
;
c)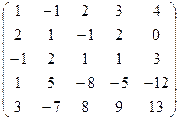 
;
d)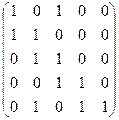 
.
Глава 3. Алгебра матриц
Прямоугольные матрицы встречаются настолько часто, что с течением времени возник самостоятельный раздел математики – теория матриц. Ее становление относят к середине прошлого века, но полноту и изящество она приобрела позднее, вместе с развитием линейной алгебры. До сих пор теория матриц остается важным инструментом исследования, хорошо приспособленным и к запросам математики. Здесь будут изложены простейшие результаты теории матриц, с более подробным изложением теории матриц можно познакомиться в книге [7].
Операции над матрицами
Операция сложения (“+”).
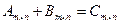, где каждый из элементов матрицы 
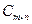равен сумме соответствующих элементов слагаемых, то есть:
.
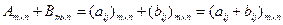Например:
.
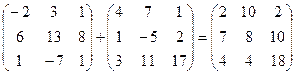Свойства операции сложения матриц:
1. 
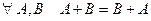
2. 
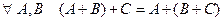
3. 
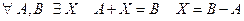
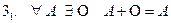
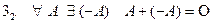
Операция умножения на скаляр (“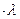 
”)
.
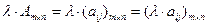Например:
.
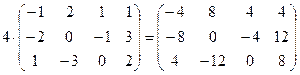Свойства операции умножения матрицы на скаляр:
4. 
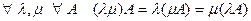
5. 
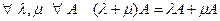
6. 
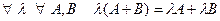
7. 
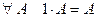
Операция умножения матриц
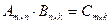, где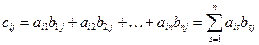 
.
Например:
.
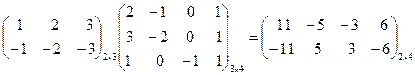Свойства операции умножения матриц:
8. 
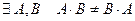, если 
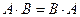, то матрицы A и B называются перестановочными.
9. 
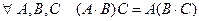
10. 
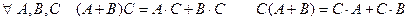
11. 
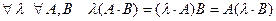
12. 
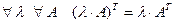
13. 
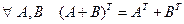
14. 
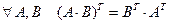
Докажем какое-нибудь из свойств операций над матрицами, например, ассоциативность их умножения: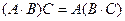 
.
Доказательство.
Требуется установить, что для произвольных матриц A, B, и C подходящего размера выполнено 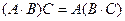. Имеем
,
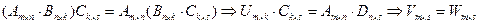т.е. правая и левая части равенства, во всяком случае, являются матрицами одного размера. Сравним их соответствующие элементы:
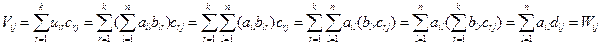
Свойство 9 доказано.
Обратная матрица
Определение. Матрицу B будем называть обратной к квадратной матрице A, если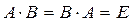 
, где E= 
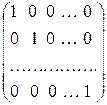- единичная матрица. Обозначение: 
.
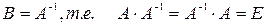Свойства обратной матрицы:
1. 
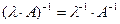
2. 
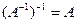
3. 
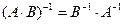
Определение. Матрицу, полученную из единичной при помощи одного элементарного строчечного или столбцового преобразования первых трех типов, будем называть элементарной матрицей.
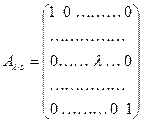
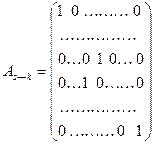
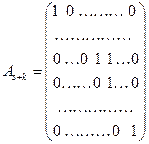
Непосредственным подсчетом можно убедиться в справедливости следующей теоремы.
Теорема. Элементарные преобразования первых трех типов данной матрицы дают тот же результат, что и умножение на элементарную матрицу, полученную с помощью строчечных или столбцовых преобразований.
Как следствие, получаем важный результат:
Теорема. Матрица обратима тогда и только тогда, когда она является неособенной.
Доказательство
А – неособенная Û r(A)=n Û можно элементарными преобразованиями строк привести матрицу А к единичной Û существуют элементарные матрицы Э1, Э2,…, Эs такие, что
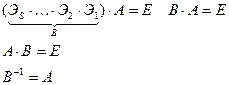
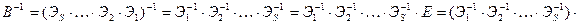
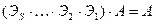. Теорема доказана.
Данная теорема дает нам способ вычисления обратной матрицы: приписываем справа (через черту) к матрице A единичную и с помощью элементарных преобразований строк приводим матрицу A к единичной. Тогда справа от черты стоит матрица A-1:
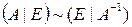
Пример.
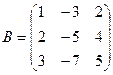
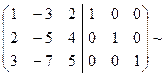
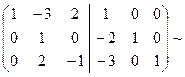
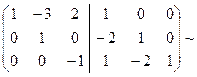
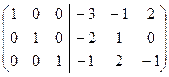Þ B-1= 