Статистическое сравнение двух выборочных средних

по t –критерию Стьюдента при неравнозначных выборках

Если объёмы выборочных совокупностей неравны (выборки неравнозначные), то критерий t- Стьюдента определяется по формуле:

t_ф= ,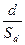

где 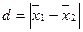, т.е. разность между сравниваемыми средними; S_d – ошибка разности выборочных средних.

S_d = ,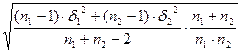

где n₁ и n₂ –объёмы сравниваемых выборочных совокупносте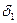й; и 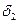- значение стандартного отклонения.

Пример расчета вспомогательных величин для вычисления t- критерия фактического приведен в таблице 4.5

Таблица 4.5 Статистическое сравнение двух выборочных средних по t- критерию Стьюдента

Фамилия	Объём выборки n, шт.	Средняя величина xi, cм.	Стандартное отклонение, σ, cм.	t факт	t 05/01
Иванов		24,45	8,09	6,23	1,96/2,58
Смирнов		22,02	4,08

.

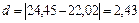S_d= .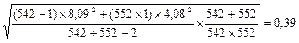

t_ф= .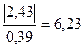

Фактическое значение t- критерия (t _Ф) сравнивается с t_St на1% и 5%-ном уровне значимости.

t _{05/ 01} определяем по приложению 1 учебника (Герасимов, Хлюстов), исходя из числа степеней свободы.

Формула для вычисления числа степеней свободы имеет вид: .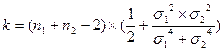

Для приведенного примера,

к = (542+552-2)×( 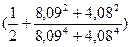= 566 следовательно, t_{05/ 01} = 1,96/2,58.

Так как t_факт(6,23) больше t₀₁ , Н₀-гипотеза отвергается, следовательно, различия существенные.

Статистическое заключение

В результате сравнения выборочной средней Иванова со средней Смирнова делаем заключение о несущественности различий между ними, т.к t_ф больше t_01.

В курсовой работе произвести сравнительную оценку со средними пятерых студентов.

Дисперсионный анализ

При исследовании причинно-следственных отношений между явлениями используется дисперсионный анализ. Дисперсионный анализ разработан английским ученым Р. А. Фишером. Он открыл закон распределения отношений средних квадратов отклонений (дисперсий).

F_ф = S₁ / S₂,

где F_ф – расчетное значение F- критерия Фишера; S₁ – средний квадрат (отклонений) выборочных средних; S₂ – средний квадрат всех объектов.

Эксперимент (опыт) нельзя спланировать, не зная основ дисперсионного анализа. При дисперсионном анализе одновременно обрабатываются данные нескольких выборок. Каждая выборка представляет собой вариант опыта. Вариантов выборок может быть несколько. Желательно вариантами опыта охватить весь диапазон возможных изменений искомого (результирующего) признака. Эти выборки (варианты опыта) составляют единый статистический комплекс. Статистический комплекс оформляется в виде рабочей таблицы.

Сущность дисперсионного анализа - это расчленение общей в опыте суммы квадратов отклонений и общего числа степеней свободы на части, которые соответствуют структуре эксперимента. При этом оценка значимости взаимодействия изучаемых факторов оценивается по F – критерию Фишера.

Рассмотрим однофакторный статистический комплекс, который состоит из нескольких независимых выборок.

L вариантов опыта, в котором общая изменчивость изучаемого признака оценивается дисперсией C_y.

C_y – общая изменчивость. Она расчленяется на две составляющие:

C_v – варьирование между выборками (вариантами опыта);

C_z – варьирование внутри выборок, внутри вариантов.

Формула изменчивости признака:

C_y = C_v + C_z ,

где C_v–обусловлена действием изучаемых факторов;

C_z – характеризует случайное варьирование, т. е. ошибку эксперимента.

Согласно определению сущности дисперсионного анализа, общее число степеней свободы, равное ν = N – 1 также делится на части. Первая часть – степени свободы для вариантов: ν = l – 1. Вторая часть – степень свободы для случайного варьирования: N – l.

Общая формула числа степеней свободы:

(N – 1) = (l – 1) + (N – l)

При обработке однофакторных комплексов, когда варианты (выборки) имеют ''n'' организованных повторений, общая сумма квадратов разлагается на три части: С_р – варьирование повторений; С_v – варьирование вариантов; С_z – случайное варьирование.

C_y = C_p + C_v + C_z

(N – 1) = ( n – 1) + ( l –1 ) + ( n – 1) + ( l – 1).

Найдем сумму квадратов отклонений по данным статистического комплекса с '' l '' вариантами и ''n'' повторностями.

В исходной таблице определяют суммы по повторениям p, по вариантам V и общую сумму всех наблюдений ∑ x.

Затем вычисляем:

- общее число наблюдений: N = l × n;

- корректирующий фактор: C = ( ∑ x )² / N;

- общая сумма квадратов: C_y = ∑ ( x )² – C;

- сумма квадратов для повторений: C_p = ( ∑ p² / l ) – C;

- сумма квадратов для вариантов: C_v =( ∑ V² / n) – C;

- сумма квадратов для ошибки: С_z = C_y - C_v .

Сумму квадратов отклонений для вариантов C_v и для ошибки C_z делят на соответствующие им степени свободы, т. е. приводят к сравниваемому виду – к одной степени свободы вариаций.

Получаем два средних квадрата дисперсии:

s_v² = C_v / l – 1,

s_z² = C_z / (n – 1) × (l – 1)

Оценка значимости воздействия изучаемых факторов осуществляется по F – критерию Фишера:

F_ф = s_v² / s_z².

Если F_ф > F₀₁, то различия между вариантами существенны. Если F_ф < F₀₅ , то различий нет.

Если F₀₅< F_ф < F₀₁, нужно увеличить число повторностей, не увеличивая числа вариант.

Если F_ф ≥ F₀₁ , то приступаем ко второй части анализа – проведем дополнительную оценку существенности частных различий.

Критерий НСР указывает предельную ошибку для разности двух выборочных средних.

Если фактическая разность ( d ) между средними по вариантам больше или равна НСР ( d ≥ НСР ), то она существенна ( значима ).

Если d < НСР – разность между средними не существенна.

Чтобы определить НСР необходимо по данным дисперсионного анализа вычислить обобщенную ошибку средней по опыту:

.

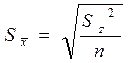Ошибку разности средних:

,

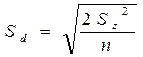где S² – остаточный средний квадрат из таблицы дисперсионного анализа;

n – число повторностей сравниваемых вариантов.

Если сравнивают группы вариантов (неодинакового размера) - неравномерные комплексы, ошибку разности вычисляют по формуле:

.

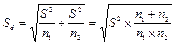Подставляя значения S_d в формулу НСР, получаем:

НСР₀₅ = t₀₅ × S_d; НСР₀₁ = t₀₁ × S_d; НСР₀₀₁ = t₀₀₁ × S_d._.

при этом t₀₅ – это t критерий Стьюдента на 5 % уровне значимости, который берётся по числу степеней свободы дисперсии остатка из учебника.

В конечном итоге строится таблица с ранжированием вариантов по росту от большего к меньшему.

После этого сравнивают лучший вариант с применяемым в производстве раньше.