Построение сечения конуса и его развертки

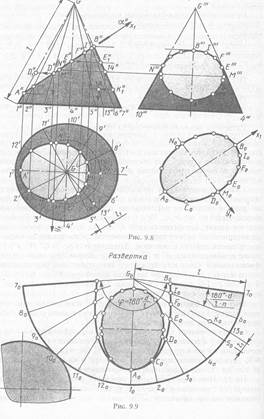
Рис. 10

Развертка боковой поверхности прямого кругового конусапред­ставляет собой круговой сектор с углом φ = d/l × 180 ° при вершине, где d - диаметр основания, l - длина образующей конуса. Пост­роение сектора (рис. 10 внизу) выполняют с разбивкой его на равные части соответственно разметке образующих на чертеже (см. рис. 10 конуса).

Используя положение образующих на чертеже и на развертке находят положение точек на развертке при помощи натуральных величин отрезков от вершины до соответствующих точек линии пересечения на чертеже. При этом расстояния G₀A₀ и G₀B₀ соответ­ствуют фронтальным проекциям G"А " С"В". Отрезки образующих от вершины до других точек проецируются на фронтальную плос­кость проекций с искажениями. Поэтому их натуральную величину находят вращением вокруг оси конуса до положения, параллельного фронтальной плоскости проекций. Например, положение точки D₀ на развертке найдено при помощи отрезка G "D₁" - натуральной величины образующей от вершины G до точки D точки E₀, - при помощи отрезка G"Е₁" (или G'"E'").

Полная развертка поверхности усеченного конуса состоит из трех частей: 1) развертки боковой поверхности, ограниченной дугой окружности радиуса l, кривой B₀I₀F₀E₀D₀C₀A₀ и симметричной ей; круга основания; 3) натурального вида фигуры сечения.

На рис. 10 (вверху) показано построение фронтальной и горизонтальной проекций точки К по изображению К₀ этой точки на развертке (рис.10). Для построения проведена образующая G₀13₀ через точку К₀ на развертке. С помощью отрезка l₁ построена горизонтальная проекция 13'. Через нее проведены горизонтальная G' 13' и фронталь­ная G"13 " проекции образующей G - 13. Отрезок G₀K₀ = G"K₁" на проекции образующей G "7 ". Обратным вращением построена фронтальная проекция К" точки К на фронтальной проекции образующей G"13".Горизонтальная проекция К' построена с помощью линии связи.

Построение сечения шара

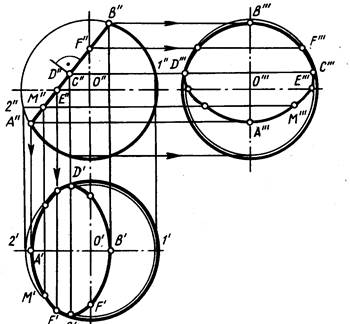
Рис. 11

На рис. 11 показано построение проекций не­которых точек.

Проекции С' и D' построены на горизонтальной проекции параллели радиуса 0'1', построенной с

помощью про­екции 1". Проекция С'" и D'" построены на профильной проекции окружности, проведенной на сфере через проекции C"(D") так, что плоскость окружности параллельна плоскости проекций.

Проекция Е' является точкой касания эллипса (горизонтальной проекции окружности среза) и экватора сферы. Она построена в про­екционной связи на горизонтальной проекции экватора по фрон­тальной проекции Е".

Горизонтальная проекция М' произвольной точки на линии среза построена с помощью параллели радиуса О'2' , фронтальная проекция которой проходит через проекции М "и 2" . Проекция F "является точкой касания эллипса (профильной про­екции окружности среза) и профильной проекции очерка сферы.

Если плоскость, пересекающая сферу, является плоскостью общего положения, то задачу решают способом перемены плоскос­тей проекций. Дополнительную плоскость проекций выбирают так, чтобы обеспечить перпендикулярность ее и секущей плоскости. Этопозволяет упростить построение линии пересечения.

Построение сечений тора

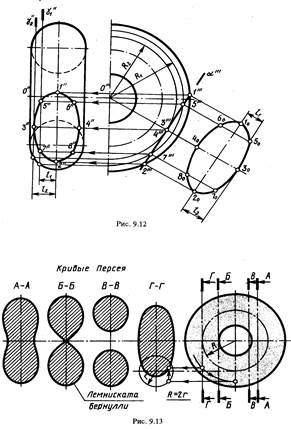
Рис. 12

В примере на рис. 12 показано применение вспомогательных плоскостей γ₁(γ₁") и γ₂(γ₂") , перпендикулярных оси тора, для построения линии пересечения и натурального вида фигуры сечения поверхности тора плоскостью α (α'"). Тор на рис.12 имеет два изображения - фронтальную проекцию и половину профильной проекции.

Полуокружность радиуса R₂ (профильная проекция линии пересечения тора вспомогательной

плоскостью γ₂) касается проекции плоскости α(следа α'"). Тем самым определяются профильная проекция 3'" и по ней фронтальная проекция 3'" одной из точек проекции искомой линии пересечения. Полуокружность радиуса R₁ - профильная проекция линии пересечения тора вспомогательной плоскостью γ₁ . Она пересекает профильную проекцию плоскости α (след α'") в двух точках 5'" и 7'" - профильных проекциях точек линии пересечения. Проводя аналогичные пост­роения, можно получить необходимое количество проекций точек для искомой линии пересечения. Используем найденные точки для построения натурального вида фигуры сечения. Фигура сечения тора плоскостью, параллельной его оси, имеет оси и центр симметрии. При ее построении использованы расстояния l₁ и l₂ на фронтальной проекции для нанесения точек 5₀, 7₀ и 3₀.

Точки 6₀ , 8₀ и 4₀ построены как симметричные. Построенная кривая пересечения поверхности тора плоскостью выражается ал­гебраическим уравнением 4-го порядка.

Кривые пересечения тора с плоскостью, параллельной оси, приведены на рис.12 внизу. Они имеют общее название - кривые Персея (Персей — геометр Древней Греции). Это кривые четвертого порядка. Вид кривых зависит от величины расстояния от секущей плоскости до оси тора.