Электрическое поле системы зарядов на больших расстояниях

Пусть задано некоторое распределение заряда , выберем начало отсчёта внутри заданного объёма.

-точка наблюдения, в ней будем считать потенциал.

Здесь, ради получения аналитического выражения пойдём на приближение: точка наблюдения далека по сравнению с объёмом системы зарядов.

Разложим функцию в ряд Тейлора:

Мы используем несколько членов этого разложения, кол-во которых зависит от требуемой точности и от малости

Под интегралом стоит . Для имеем:

Рассмотрим

Тогда

Здесь

Рассмотрим некоторые члены этого разложения:

Первый член:

- это кулоновский потенциал (заряд 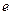сосредоточен в точке начала координат).

Второй член:

сам интеграл даёт дипольный момент системы:

- потенциал, который создаёт в точке наблюдения диполь , расположенный в точке начала координат

Третий член:

Рассмотрим

Последнее слагаемое при интегрировании даст нуль, т.к.

Вспомним выражение:

При получаем:

Здесь точка наблюдения не лежит в объёме с зарядами, тогда всегда.

Тогда при интегрировании даст нулевой вклад. В результате получаем:

Полученный интеграл – это

Мы получили потенциал квадрупольного типа. Можно дальше рассматривать члены разложения, разлагаем по мультипольным моментам. Когда оборвать ряд зависит от малости .

, имеет порядок

Чем меньше этот параметр, тем меньше членов надо учитывать в разложении.