Колоколообразный (гауссовский) импульс
Импульс определяется выражением (рис.2.7)
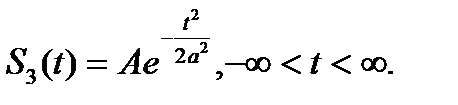
(2.23)
Постоянная 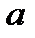 имеет смысл половины длительности импульса определяемой на уровне
имеет смысл половины длительности импульса определяемой на уровне 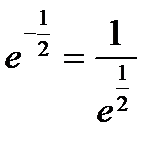 от амплитуды импульса. Таким образом, полная длительность импульса
от амплитуды импульса. Таким образом, полная длительность импульса 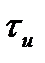 равна
равна 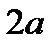 .
.
рис.2.7
Спектральная плотность импульса определяется выражением
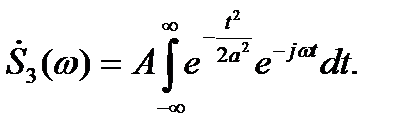
(2.24)
Для вычисления интеграла удобно в подинтегральной функции дополнить показатель степени до квадрата суммы
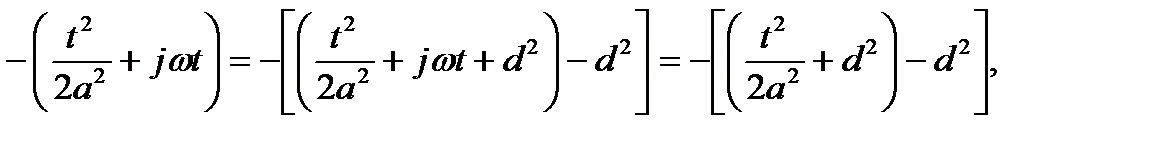
где величина 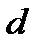 определяется из условия
определяется из условия
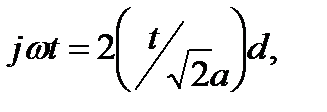
откуда
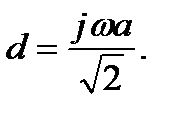 (2.25)
(2.25)
Таким образом, выражение (2.24) можно привести к виду
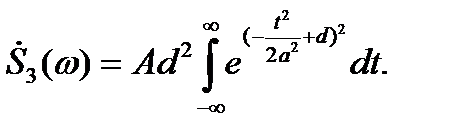
Переходя к новой переменной 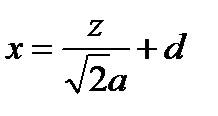 , получаем
, получаем
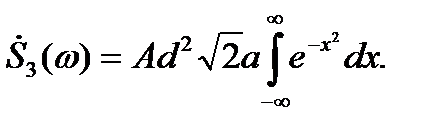
Учитывая, что входящий в это выражение интеграл равен 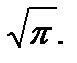 , окончательно получаем
, окончательно получаем
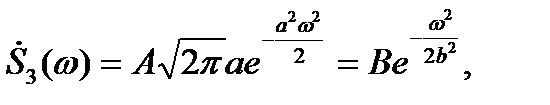 (2.26)
(2.26)
где 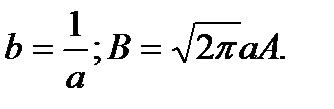
График этой функции изображен на рис.2.8
рис.2.8
Гауссовский импульс и его спектр выражаются одинаковыми функциями и обладают свойствами симметрии: для получения одной из них по заданной другой достаточно заменить 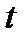 на
на 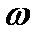 или наоборот. При этом спектральная полоса, определяется на уровне
или наоборот. При этом спектральная полоса, определяется на уровне 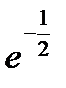 от максимального значения, равна
от максимального значения, равна 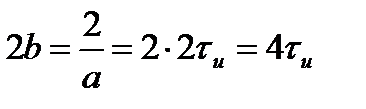 , а коэффициент
, а коэффициент 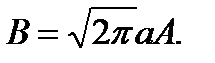
2.5.4 Импульс вида 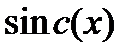
Импульс определяется выражением (рис.2.9)
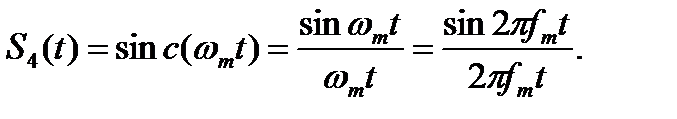 (2.27)
(2.27)
рис.2.9
Вместо вычисления спектральной плотности воспользуемся свойством взаимозаменяемости 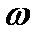 и
и 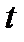 в преобразованиях Фурье для четных функций времени.
в преобразованиях Фурье для четных функций времени.
Спектральная плотность импульса определяется формулой
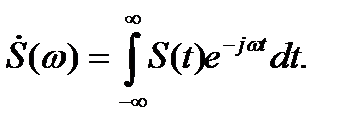
Из спектральной плотности прямоугольного импульса, после замены 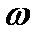 на
на 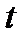 и
и 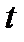 на
на 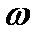 заданной функции будет соответствовать спектр прямоугольной формы (рис.2.10). Остается лишь найти площадь этого спектра и его уровень.
заданной функции будет соответствовать спектр прямоугольной формы (рис.2.10). Остается лишь найти площадь этого спектра и его уровень.
рис.2.10
Для этого сопоставим абсциссу 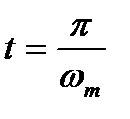 с аналогичной абсциссой
с аналогичной абсциссой 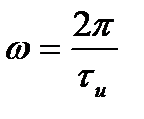 . При замене
. При замене 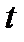 на
на 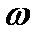 (или наоборот) необходимо исходить из соответствия
(или наоборот) необходимо исходить из соответствия 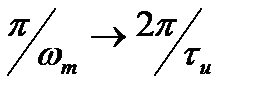 , т.е.
, т.е. 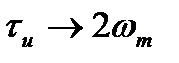 , откуда следует, что
, откуда следует, что 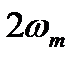 есть искомая ширина спектра
есть искомая ширина спектра 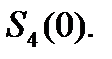
Уровень спектра можно определить по его значению в точке 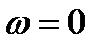 , для которой
, для которой 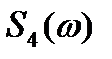 равно площади импульса:
равно площади импульса:
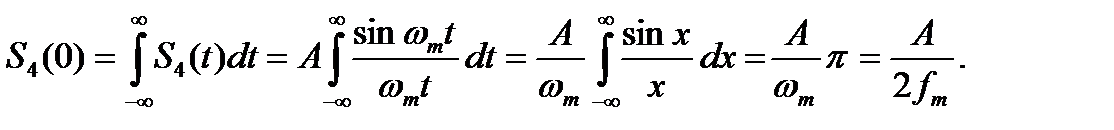
Итак, окончательно
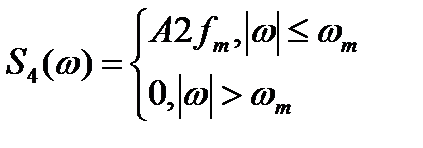
(2.28)
