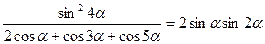Тема 1.1 Преобразования алгебраических выражений, выражений, содержащих радикалы и степени с дробным показателем
Основные понятия и термины по теме: свойства степени с действительным показателем,
формулы сокращенного умножения.
План изучения темы (перечень вопросов, обязательных к изучению):
1. Свойства степеней с действительным показателем.
2. свойства корней.
3. Модуль числа.
4. Формулы сокращенного умножения.
5. Разложение многочленов на множители.
Краткое изложение теоретических вопросов:
Свойства степеней с действительными показателями
1) 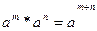 ; 2)
; 2) 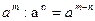 ; 3)
; 3) 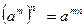 ;
;
4) 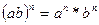 ; 5)
; 5) 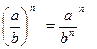 ;
; 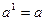 ;
; 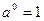 .
.
Свойства корней
1) 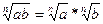 ; 2)
; 2) 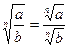 ; 3)
; 3) 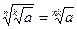 ;
;
4) 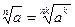 ; 5)
; 5) 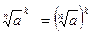 ; 6)
; 6) 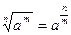
Модуль числа
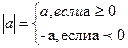
Формулы сокращенного умножения
1) 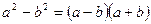 ;
;
2) 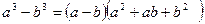 ;
;
3) 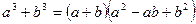 ;
;
4) 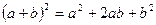
5) 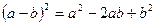
6) 
7) 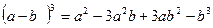
Разложение многочленов на множители
При разложении многочленов на множители используют следующие приемы:
а) вынесение общего множителя за скобки;
б) группировка членов;
в) использование формул сокращенного умножения;
г) нахождение корней многочлена.
Пример 1.Упростите выражение 2 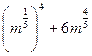
Решение:
2 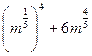 =2
=2 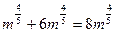
Ответ: 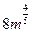
Пример 2.Вычислите 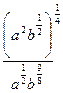 при
при 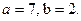
Решение:
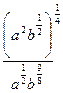 =
= 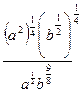 =
= 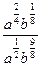 =
= 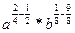 =
= 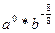 =
= 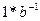 =
= 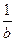
Если 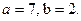 , то
, то 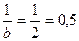
Ответ: 0,5.
Пример 3.Вычислите 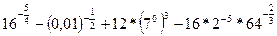 .
.
Решение:
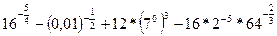 =
= 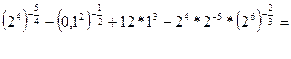
= 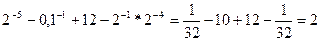
Ответ: 2.
Пример 4.Упростить выражение 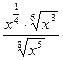 .
.
Решение:
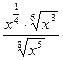 =
= 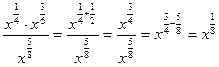
Ответ: 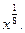
Лабораторные работы/Практические занятия
не предусмотрены
Задания для самостоятельного выполнения:
1.Найдите значение числового выражения 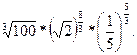
Ответ: 0,8
2.Вычислите 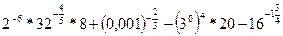
Ответ: 80.
3.Найдите значение числового выражения
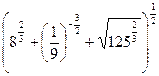
Ответ: 6.
4.Упростить  .
.
Ответ: 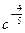 .
.
Тема 1.2 Преобразования тригонометрических выражений.
Основные понятия и термины по теме:основные формулы тригонометрии
План изучения темы (перечень вопросов, обязательных к изучению):
1. Связь между функциями одного угла.
2. Функции суммы и разности углов.
3. Преобразование суммы функций в произведение.
4. Преобразование произведения функций в сумму.
5. Функции кратных углов.
6. Формулы понижения степени.
Краткое изложение теоретических вопросов:
Связь между функциями одного угла
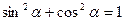 ;
; 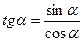 ;
; 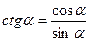 .
.
Функции суммы и разности углов
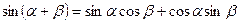 ;
;
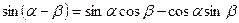 ;
;
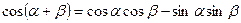 ;
;
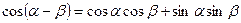 .
.
Преобразование суммы функций в произведение
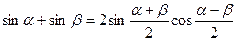 ;
;
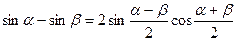 ;
;
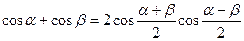 ;
;
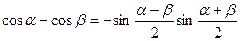 .
.
Преобразование произведения функций в сумму
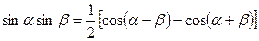 ;
;
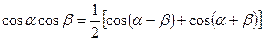 ;
;
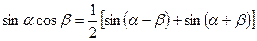 .
.
Функции кратных углов
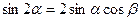 ;
; 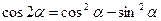
Функции понижения степени
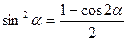 ;
; 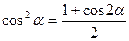
Приведенные формулы являются базовыми, и их необходимо помнить. Другие, встречающиеся в справочниках, соотношения выводятся из базовых формул, и их запоминать не стоит.
Пример 1.Упростите выражение
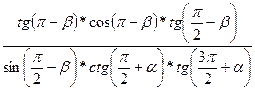 .
.
Решение:
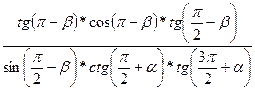 =
= 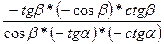 =1
=1
Ответ: 1.
Пример 2.Упростите выражение 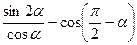 .
.
Решение: 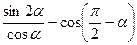 =
= 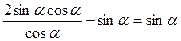 .
.
Ответ: 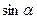 .
.
Лабораторные работы/Практические занятия
Не предусмотрены
Задания для самостоятельного выполнения:
1. Вычислите 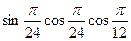 .
.
Ответ: 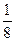 .
.
2. Упростите выражение 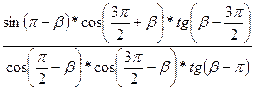 .
.
Ответ: -1.
3. Докажите тождество