Математическая модель летательного аппарата

Для исследования управления БАК при решении задачи боевого применения НАСП по должны быть созданы математические модели ЛА, являющегося объектом управления, а также системы управления полетом. Также должны быть сформированы собственно законы управления ЛА в продольном, боковом и скоростном каналах, отвечающие требованиям, предъявляемым к эффективности БАК при боевом применении НАСП.

Управление полетом ЛА сводится к управлению параметрами различных режимов полета, представляющими собой совокупность координат ЛА в фазовом пространстве. Приведение фазовых координат к заданным величинам является главной задачей системы управления полетом ЛА. При движении ЛА, вследствие воздействия на него ряда неконтролируемых возмущений, его фазовые координаты отклоняются от требуемых значений. Устранение этих отклонений и стабилизация параметров движения ЛА составляют другую задачу системы управления полетом.

Из теоретической механики известно, что движение свободного тела в пространстве можно в общем случае представить состоящим из поступательного движения центра тяжести тела и вращения тела около центра тяжести.

Введем понятие внешних сил 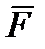, действующих на ЛА. Внешними силами, действующими на ЛА, являются: полная аэродинамическая сила, представляющая собой геометрическую сумму подъемной силы 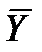, силы лобового сопротивления 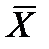и боковой силы 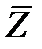, а также сила тяги двигателя 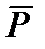и сила тяжести .

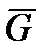Введем также понятие вектора перегрузки 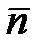, под которым будем понимать отношение геометрической суммы всех внешних сил, действующих на ЛА, кроме силы тяжести и силы инерции к силе тяжести. При расчетах будем пользоваться не самим вектором перегрузки 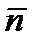, а его проекциями на оси связанной системы координат – значениями продольной n_x, нормальной n_y и боковой n_z перегрузок:

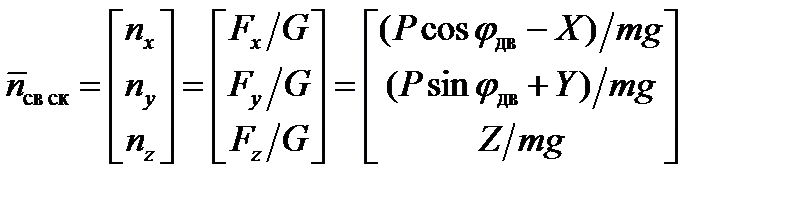
где 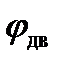– угол установки двигателя ЛА.

Уравнением движения центра масс является уравнение изменения количества движения, которое в инерциальной системе координат имеет вид:

,

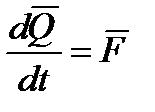где 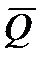– вектор количества движения:

,

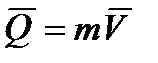где 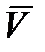– абсолютная линейная скорость центра масс ЛА;

m – масса ЛА.

В подвижной системе координат, вращающейся со скоростью , это уравнение запишется в виде:

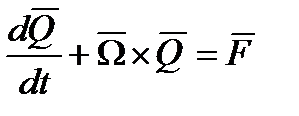, (11)

где 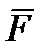– главный вектор системы сил, действующих на ЛА;

– вектор угловой скорости подвижной системы координат относительно инерциальной системы координат;

;

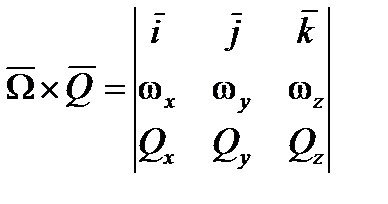ω_x, ω_y, ω_z, Q_x, Q_y, Q_z – соответствующие проекции векторов и на оси подвижной системы координат.

Проецируя векторное уравнение (11) на оси подвижной системы координат, получим:

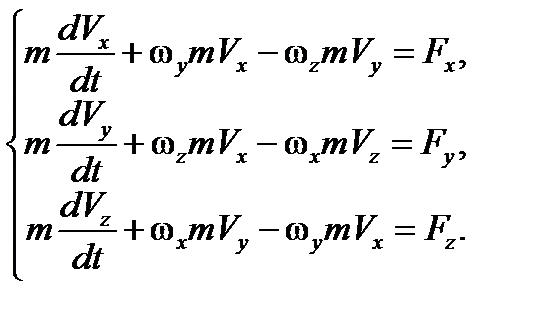
При анализе устойчивости движения необходимо учитывать вращение ЛА относительно его центра тяжести и моменты аэродинамических сил, вызывающие это вращение. В этом случае ЛА рассматривается уже как твердое тело, и в дополнение к трем уравнениям изменения количества движения берутся три уравнения, выражающие закон изменения момента количества движения. При этом в качестве подвижной системы координат используют связанную с ЛА систему координатных осей, начало которой совмещают с центром тяжести ЛА. Также с достаточной степенью достоверности можно считать, что эти оси направлены по главным центральным осям инерции ЛА.

Уравнение изменения момента количества движения:

– в инерциальной системе координат:

,

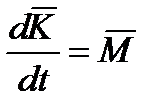где 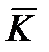– вектор момента количества движения:

;

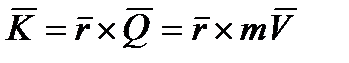– в подвижной системе координат:

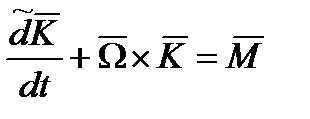; (12)

,

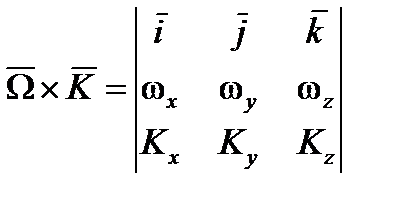где K_x K_y K_z – соответствующие проекции вектора 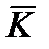на оси подвижной системы координат.

Проецируя векторное уравнение (12) на оси подвижной системы координат, получим уравнения движения ЛА относительно его центра тяжести:

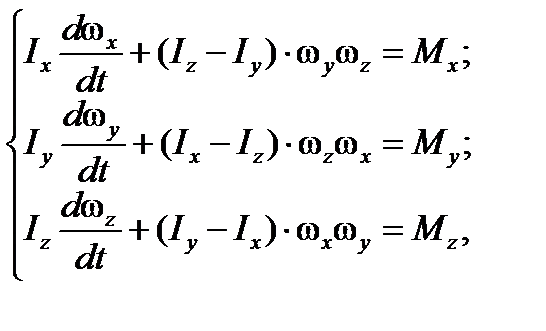
где ω_x ω_y ω_z – проекции угловой скорости вращения ЛА на главные центральные оси инерции;

M_x, M_y, M_z – проекции моментов относительно центра тяжести ЛА на те же оси;

I_x, I_y, I_z – главные центральные моменты инерции ЛА.

Таким образом, можно составить математическую модель движения ЛА, учитывая кроме всего прочего и случайные воздействия. Движение ЛА как твердого тела в пространстве описывается двенадцатью дифференциальными уравнениями первого порядка, из них [10]:

- три динамических уравнения движения центра масс;

- три динамических уравнения Эйлера;

- три кинематических уравнения Эйлера;

- три кинематических уравнения траектории.

Для подвижной системы координат, связанной с ЛА, эти уравнения имеют вид:

;

;

;

;

,

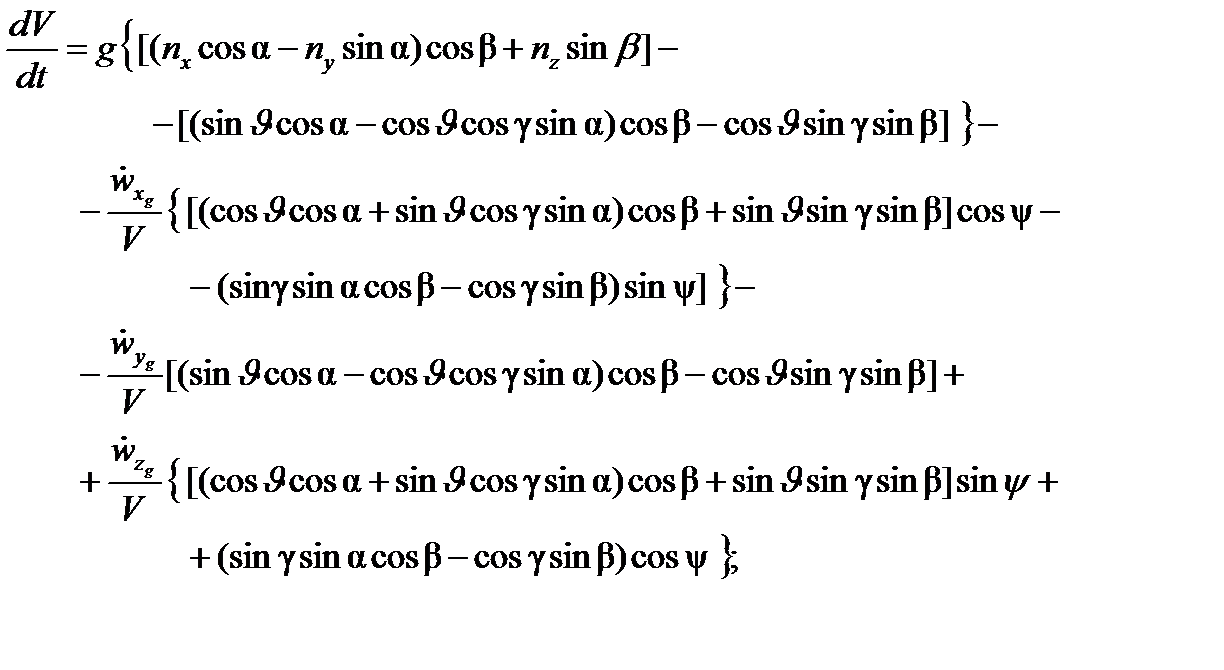
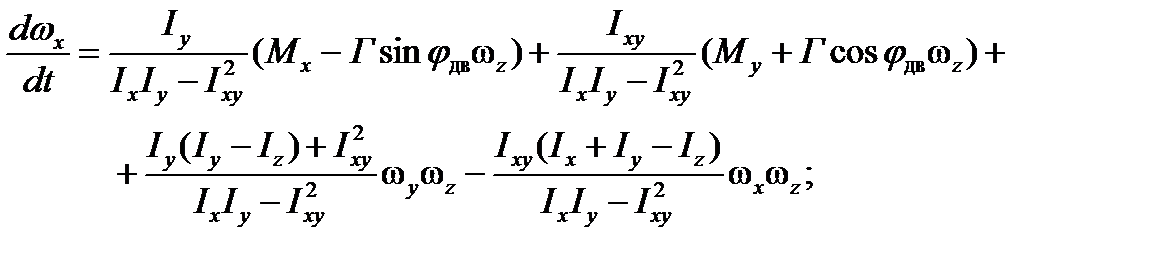
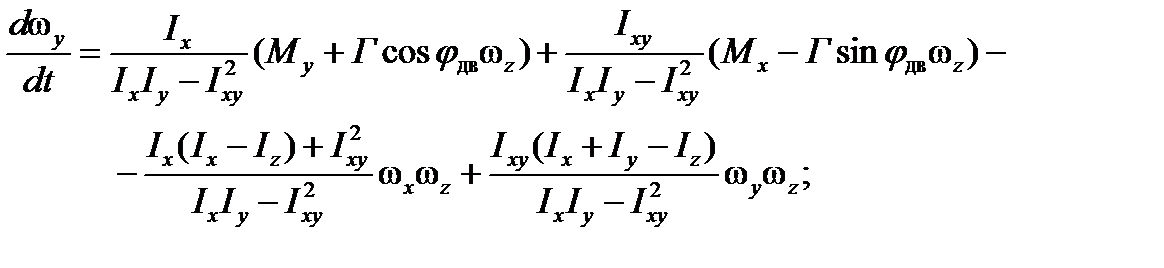
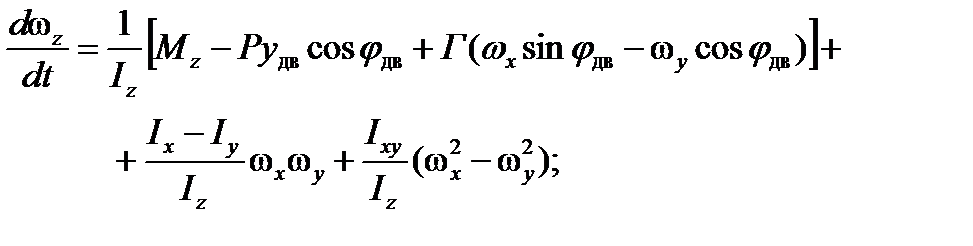
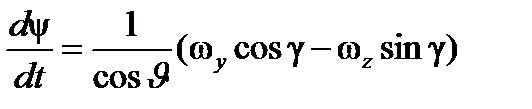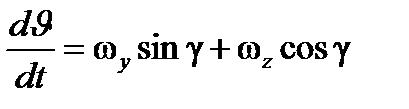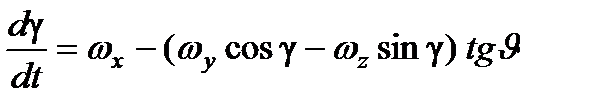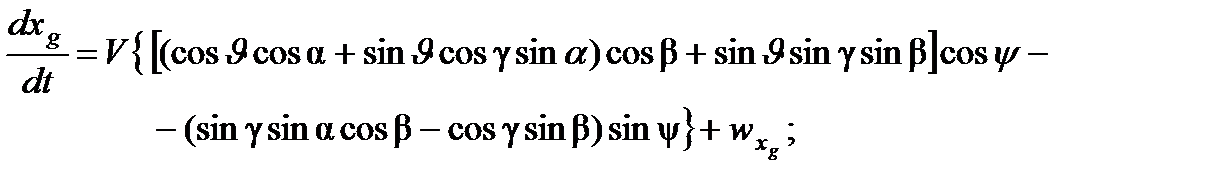
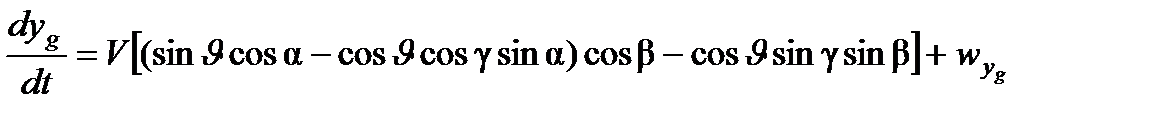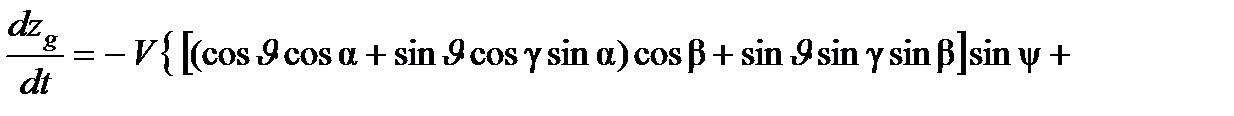
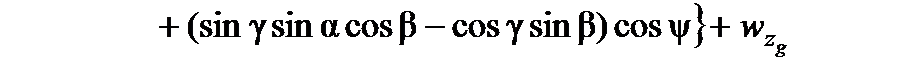где 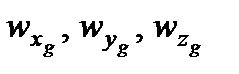– составляющие вектора случайных возмущающих воздействий на полет ЛА.

В уравнениях сделаны следующие допущения:

- кривизна Земли не учитывается;

- масса ЛА в процессе прицеливания постоянна m = const.

На основании анализа структуры и характеристик процесса прицеливания по НЦ можно сделать вывод о возможности упрощения полной математической модели ЛА как объекта управления. Кроме того, могут быть определены наиболее адекватные математические модели движения ЛА на каждом из этапов процесса прицеливания по НЦ.

При построении упрощенной математической модели, описывающей движение ударного БАК при применении НАСП по НЦ, могут быть приняты следующие гипотезы и допущения:

- устойчивость движения ЛА относительно его центра тяжести обеспечивается системой управления полетом, вследствие чего производными угловых скоростей вращения ЛА относительно центра масс можно пренебречь: ;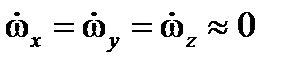

- движение в боковом канале осуществляется без скольжения: β ≈ 0;

- гироскопический момент двигателей мал: Г = 0;

- устранение отклонений параметров движения ЛА, вызванных воздействием случайных возмущающих факторов, от заданных значений обеспечивается системой управления полетом, следовательно, можно принять: , .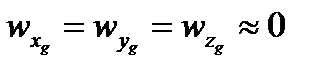

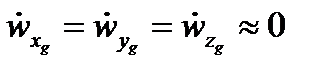Таким образом, полная математическая модель БАК как объекта управления в задаче прицеливания при применении АСП по НЦ для подвижной системы координат, связанной с ЛА, может быть приведена к следующему виду:

;

;

;

;

.

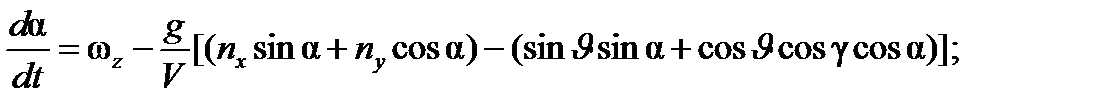
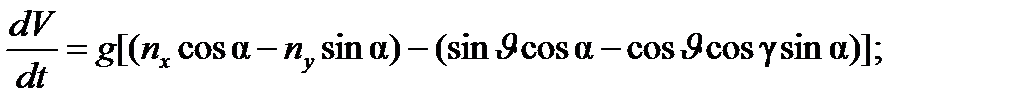
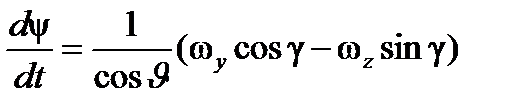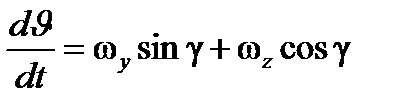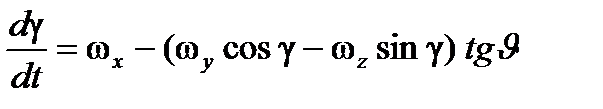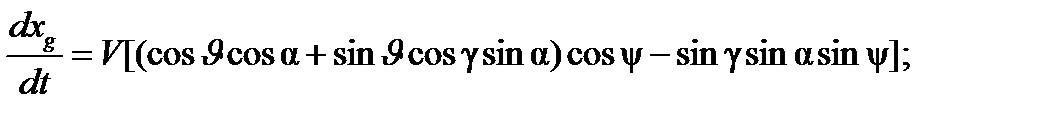
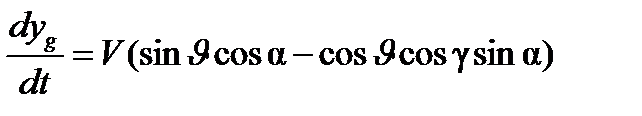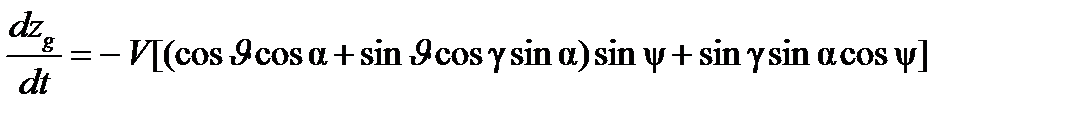Систему управления полетом в задаче прицеливания следует рассматривать в качестве совокупности динамических объектов, решающих следующие специфические задачи:

- автономные режимы системы автоматического управления (САУ), задачей которых является совместное с вычислительной системой АПрС участие в формировании потребных значений управляющих параметров в продольном, боковом и скоростном каналах для текущего режима полета ЛА;

- внутренние контуры каналов управления САУ, задачей которых является приведение сформированных значений управляющих параметров к размерности величин, характеризующих отклонение органов управления летчиком, в целях организации режимов совмещенного управления;

- система дистанционного управления (СДУ), задачей которой является обеспечение заданного качества отработки управляющих параметров за счет определения наиболее эффективных для текущего режима полета ЛА поверхностей управления и формирования соответствующих воздействий на исполнительные устройства;

- поверхности управления совместно с двигательной установкой, участвующие в процессе формирования сил и моментов, которые в свою очередь определяют значения правых частей кинематических уравнений движения ЛА.

При решении задач автоматического управления ударным БАК в режимах прицеливания к внутренним контурам САУ предъявляются следующие требования:

- реализация режимов автоматического управления при заданных диапазонах изменения управляющих параметров;

- обеспечение заданного уровня быстродействия при отработке управляющих воздействий;

- обеспечение заданного уровня качества переходных процессов при отработке управляющих воздействий, в том числе перерегулирование должно составлять не более 10 %.

Полагая, что выполнение последнего требования обеспечивает СДУ, что подтверждается результатами натурных испытаний современных БАК, при математическом моделировании задачи прицеливания по НЦ динамические свойства внутренних контуров САУ (и системы управления полетом ЛА в целом) могут быть представлены в виде апериодических звеньев в каждом из каналов управления.

Кроме того, вектор управления 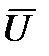фазовыми координатами ЛА [x, y, z,ψ,ϑ,γ, V]^T в задаче прицеливания по НЦ может быть сведен к трем управляющим параметрам – по одному параметру в каждом из каналов управления ЛА: 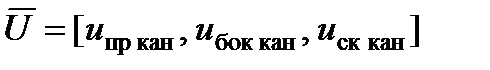. Так в продольном канале управления таким управляющим параметром является нормальная перегрузка n_y объекта; в боковом канале – угол крена γ; в скоростном канале – истинная скорость V_ист полета ЛА.

Структурная схема ЛА как объекта управления при решении задачи прицеливания по НЦ представлена на рис. 8.

Представим описание динамики внутренних контуров управления ЛА в задаче прицеливания по НЦ.

Вектор управления фазовыми координатами ЛА в продольном канале y_зад , θ_зад может быть сведен к одному управляющему параметру – заданному значению избыточной нормальной перегрузки u_{пр кан} = n_{y зад}. Рассмотрим динамические особенности внутреннего контура управления ЛА в продольном канале.

При управлении ЛА в продольном канале в автоматическом режиме вычисленное в вычислительной системе АПрС заданное значение избыточной нормальной перегрузки 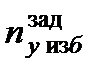объекта должно быть ограничено значениями верхней границы 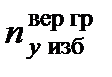и нижней границы .

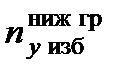Соотношение полной и избыточной нормальной перегрузки определяется следующей зависимостью:

n_{y изб =} n_{y полн} – 1,0.

В результате специального медицинского исследования физиологических особенностей человеческого организма было выявлено, что при управлении ЛА в автоматическом режиме обученный летчик способен выдерживать полную нормальную перегрузку до плюс 4,0 единиц. В случае превышения указанного значения психофизиологическая нагрузка достигает предельной величины, что может привести к потере летчиком сознания, и как следствие к срыву выполнения полетного задания. Следует также отметить, что при управлении ЛА в ручном или директорном режимах, когда летчик сознательно создает положительную перегрузку и заранее готовится к данным режимам, тренированный летчик способен переносить полную нормальную перегрузку до плюс 9,0 единиц и больше.

Значение нижней границы избыточной нормальной перегрузки 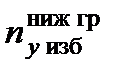объекта выбирается из следующих соображений: при управлении ЛА в автоматическом режиме величина полной нормальной перегрузки n_{y полн} не должна составить близкое к нулю значение. В подобных режимах резко снижается эффективность функционирования насосов топливной системы ЛА. В связи с указанной особенностью современных ЛА в нормативных документах время полета ЛА с отрицательными значениями избыточной нормальной перегрузки n_{y изб} строго ограничивается.

Таким образом, заданное значение избыточной нормальной перегрузки объекта 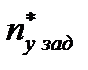на входе внутреннего контура продольного канала управления определяется следующим соотношением:

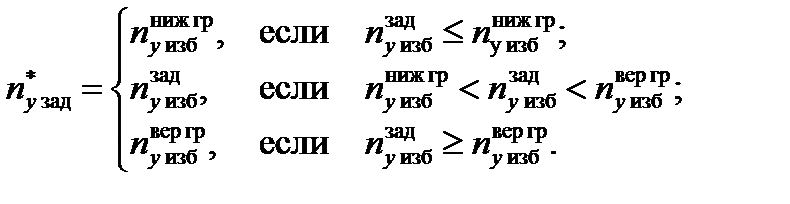
Как ранее было отмечено, динамические свойства ЛА как объекта управления в продольном канале управления могут быть представлены в виде апериодического звена вида:

,

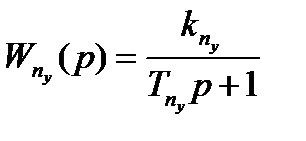где в качестве параметра управления выступает заданное значение избыточной нормальной перегрузки объекта .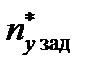

Допустимое отклонение 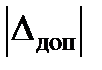, характеризующее величину допустимого относительного отклонения регулируемой координаты в установившемся режиме x_уст относительно заданного значения x_зад, принято равным 10 %.

Время регулирования t_рег – промежуток времени между моментом приложения ступенчатого воздействия и моментом времени, начиная с которого отклонение регулируемой координаты от требуемого значения остается в пределах 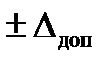, т.е. определяется соотношением:

.

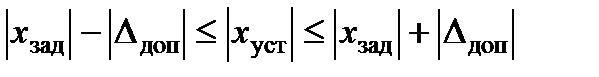Время t_рег апериодического процесса равно утроенному значению постоянной времени 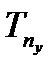и для управляющего параметра в продольном канале 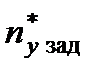определяется, исходя из располагаемой эффективности органов управления и динамических характеристик ЛА на различных режимах полета, как функция истинной скорости полета:

,

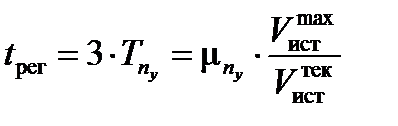где 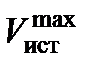– истинная скорость полета ЛА, соответствующая максимальной эффективности БАК и определяемая на основе ее оценки по высотно-скоростной диаграмме в диапазоне допустимых режимов полета;

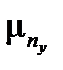– коэффициент пропорциональности, определяемый текущим режимом полета ЛА.

Графически описанная здесь передаточная функция внутреннего контура управления ЛА в продольном канале представлена на рис. 9.

Вектор управления фазовыми координатами ЛА в боковом канале z_зад, ψ_зад, γ_зад может быть сведен к одному управляющему параметру – заданному значению угла крена

u_{бок кан} = γ_зад.

При управлении ЛА в боковом канале в автоматическом режиме вычисленное в БЦВС АПрС заданное значение угла крена γ_зад должно быть ограничено по абсолютной величине следующими значениями в зависимости от текущей геометрической высоты полета :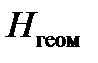

- при :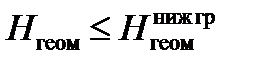

;

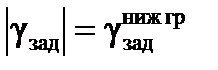- при :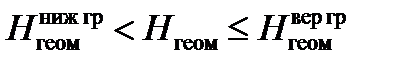

;

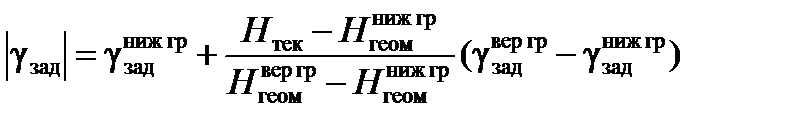- при :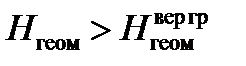

.

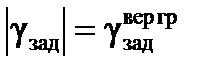Обоснование представленных здесь ограничений следующее. При выполнении полета ЛА на малых высотах предъявляются повышенные требования к его безопасности, в том числе это относится и к достоверности пилотажно-навигационной информации. Во избежание ситуации отсутствия на борту ЛА достоверной информации о геометрической высоте полета и предотвращения аварийных ситуаций вследствие потери летчиком ориентации в пространстве в автоматическом режиме управления объектом предельно допустимый угол крена ограничивается значением .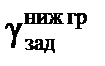

В автоматическом режиме управления объектом при больших значениях геометрической высоты полета H_геом предельно допустимый угол крена определяется значением 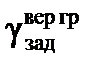, исходя из требования обеспечить в боковом канале выполнение координированного разворота без потери объектом высоты.

Таким образом, на вход внутреннего контура бокового канала управления ЛА подается сигнал 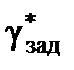, определяемый соотношением:

,

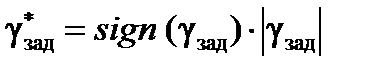где 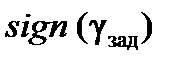– функция знака расчетного заданного значения оптимального угла крена, имеющая вид:

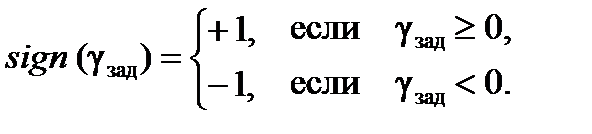
Как было отмечено, динамические свойства внутреннего контура управления ЛА в боковом канале могут быть представлены в виде типового апериодического звена:

,

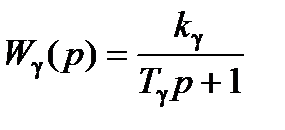где в качестве параметра управления выступает заданное значение угла крена объекта .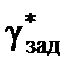

К качеству управления ЛА в боковом канале предъявляется следующее требование: время регулирования t_рег должно составлять не более заданного значения, определяемого из условий максимальной боевой эффективности, при допустимом отклонении равном 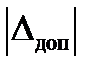= 10 %.

Отсюда следует, что постоянная времени T_γ апериодического процесса изменения управляющего параметра в боковом канале 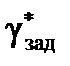должна принимать фиксированное значение. Однако поскольку эффективность аэродинамических органов управления и располагаемые динамические характеристики ЛА изменяются в зависимости от режима полета, необходимо учесть данное ограничение в виде определения функции постоянной времени 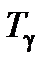, используя в качестве аргумента текущее значение истинной скорости полета.

При определении указанной функции аналогичным образом, как и при формировании внутреннего контура управления в продольном канале, вводится понятие истинной скорости полета ЛА 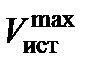, соответствующей максимальной эффективности БАК.

Максимальное граничное значение постоянной времени 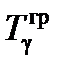апериодического процесса изменения управляющего параметра в боковом канале 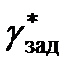определяется, исходя из требования обеспечить заданную угловую скорость вращения ЛА по крену при полном перемещении рукоятки управления в боковом направлении:

,

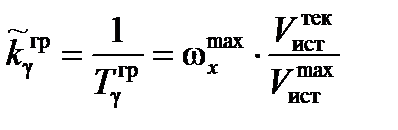где 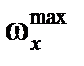– угловая скорость поперечного движения ЛА при скорости полета .

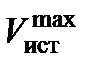Окончательно сформулируем, что постоянная времени T_γ передаточной функции 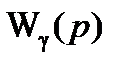апериодического звена, определяющей динамические свойства переходного процесса 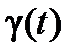управления ЛА в боковом канале, может быть представлена следующим выражением:

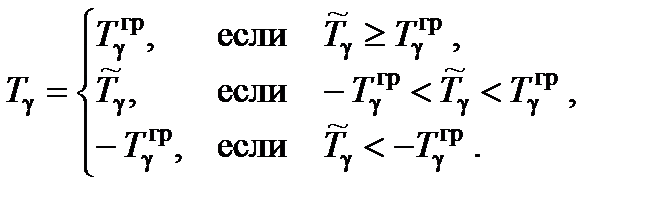
Графически описанная здесь передаточная функция внутреннего контура управления ЛА в боковом канале представлена на рис. 10.

Параметром управления ЛА в скоростном канале u_{ск кан} является истинная скорость V_ист полета. Исполнительным устройством в скоростном канале управления является автомат тяги, а объектом управления является силовая установка ЛА (см. рис. 8).

При формировании автоматического управления объектом в скоростном канале следует учитывать ограничения по скорости полета. Так, например, необходимо учитывать наименьшую скорость 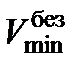полета ЛА, при которой обеспечивается безопасность применения конкретного НАСП, при заданной высоте боевого применения, которая называется минимальной безопасной скоростью боевого применения.

Кроме того, максимальная скорость боевого применения 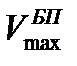ограничивается допустимой по кинетическому нагреву НАСП V_кин скоростью полета ЛА или другими условиями, связанными с устойчивостью НАСП на траектории и прочностью их элементов, а также безопасностью, определяемой требованиями несрабатывания механических пусковых устройств под действием скоростного напора. Значения максимальной скорости боевого применения приводятся в нормативных документах по эксплуатации БАК и КАВ. В случае, когда максимальная располагаемая скорость 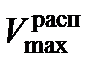объекта не превышает величины V_кин, скорость боевого применения на данном типе ЛА ограничена максимально допустимой 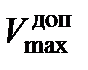скоростью полета. Таким образом, максимальная скорость боевого применения 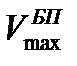определяется следующим соотношением:

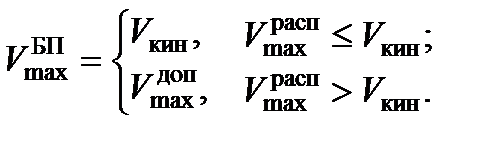
Окончательно имеем, что заданное значение истинной скорости полета V_зад определяется следующим образом:

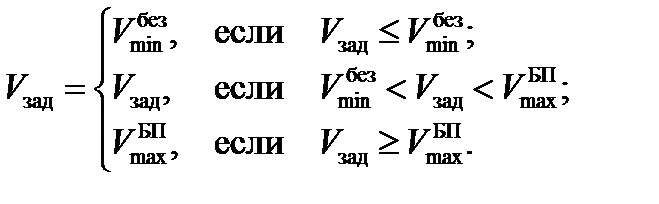
Как уже было отмечено, динамические свойства внутреннего контура управления ЛА в скоростном канале также могут быть представлены в виде типового апериодического звена:

,

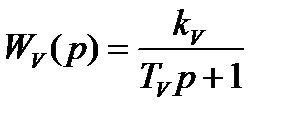где в качестве параметра управления выступает заданное значение истинной скорости 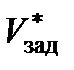полета объекта.

Истинная скорость полета, являющаяся параметром управления ЛА в скоростном канале, представляет собой медленно изменяющуюся величину. Так к качеству управления ударным БАК в скоростном канале предъявляется следующее требование: время регулирования t_рег должно составлять не более заданного значения, определяемого из условий максимальной боевой эффективности, при допустимом отклонении равном 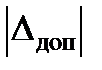= 10 %.

Отсюда следует, что постоянная времени T_V апериодического процесса изменения управляющего параметра в скоростном канале V_зад должна принимать фиксированное значение. Однако поскольку силовая установка ЛА обладает вполне определенными высотно-скоростными характеристиками на различных режимах полета, объективно существуют ограничения динамики переходных процессов в канале управления скоростью полета, связанные с соотношением потребных и располагаемых значений тяги двигателей. Таким образом, данные свойства силовой установки учитываются в виде ограничения темпа 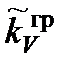разгона и торможения объекта, который не может превышать по абсолютной величине определенного значения.

Следовательно, необходимо учесть указанное ограничение в виде определения функции постоянной времени 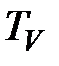вида:

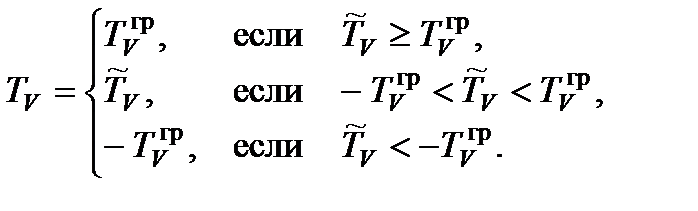
Графически описанная здесь передаточная функция внутреннего контура управления ЛА в скоростном канале представлена на рис. 11.