Матрицы соединений и узловых проводимостей

Матрицы соединений (инциденций) применяются для отражения характера соединений ветвей схемы в узлах и независимых контурах.

Первая матрица соединений А устанавливает связь между узлами и ветвями схемы. В данной матрице соединений строки соответствуют номерам узлов, а столбцы – номерам ветвей. Элементы 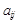матрицы соединений А, располагаемые на пересечении строки i и столбца j, называются коэффициентами соединений (инцидентности). Они могут принимать только одно из трех значений: +1,-1,0.

Коэффициент , если i –й узел является начальной вершиной j –й ветви. Если i-й узел является конечной вершиной j-й ветви, то . Когда ветвь j не присоединяется к узлу i, то .

Первая матрица соединений служит для составления узлового уравнения состояния.

Вторая матрица соединений устанавливает связь между ветвями и независимыми замкнутыми контурами схемы. В ней строкам соответствуют номера независимых замкнутых контуров, а столбцам – номера ветвей. Как и для матрицы А, элементы (коэффициенты соединений) матрицы В могут принимать только одно из трех значений: +1,-1,0. Коэффициент , если направление ветви j совпадает с направлением i-ого независимого замкнутого контура. Если их направления противоположны, то , и , когда ветвь j не входит в состав i-ого независимого замкнутого контура.

При расчетах установившихся режимов работы электрической системы в ней обычно выделяется базисный по напряжению узел, т.е. узел с заданным уровнем напряжения. Зная напряжение базисного узла и величины источников тока, можно найти все остальные параметры режима системы.

Для выполнения практических расчетов большой интерес представляет обобщенные пассивные параметры схем: матрицы узловых сопротивлений и проводимостей; матрицы контурных сопротивлений и проводимостей и другие.

Эти параметры характеризуют схему в целом и определяются натуральными параметрами схемы (пассивными).

Матрица узловых проводимостей определяется через первую матрицу соединений и матрицу сопротивлений ветвей как

где - транспонированная первая матрица инцидентности,

- матрица сопротивлений ветвей схемы.

Матрица является диагональной: элементами главной диагонали служат сопротивления ветвей схемы, остальные элементы данной матрицы – нули.

Пример: для схемы, приведенной на рисунке 4.1, записать первую и вторую матрицы соединений и определить матрицу узловых проводимостей. Узел 0 принять за базисный узел. Сопротивления ветвей следующие: .

Рисунок 4.1 – Граф электрической сети

Решение.

Составляем первую матрицу соединений. Так как узел 0 является базисным, то матрица M будет иметь 2 строки и 3 столбца, т.е. будет являться прямоугольной:

Матрица, ей транспонированная:

Поскольку схема имеет один замкнутый контур, то вторая матрица соединений будет иметь одну строку и три столбца (по числу ветвей):

Запишем матрицу сопротивлений ветвей

Затем определим матрицу , обратную матрице . Матрица определяется легко, т.к. матрица является диагональной

На следующем этапе определяется матрица узловых проводимостей

При выполнении задач № 1, 2 рекомендуется использовать литературу 1,8,9.