Линейная перспектива. Фронтальная перспектива.
Вданном модуле студентам даются основные определения и правила построения фронтальной перспективы. А также возможности их применения на практике.
Фронтальная перспектива - один из видов линейной перспективы. Ее основное положение - это фронтальное (параллельное) расположение объекта к наблюдателю. При этом перспективном построении все параллельные линии, идущие под прямым углом к картинной плоскости, сходятся в центральной точке схода, лежащей на линии горизонта.
Все параллельные между собой линии, расположенные параллельно картинной плоскости, не имеют точек схода.
Как уже отмечалось ранее в основе линейной перспективы лежит метод центрального проецирования, заключающийся в том, что перспективное изображение получается на плоскости при помощи прямых, проведенных из одной точки, называемей центром проекций S (или точкой зрения). Лучи идущие из точки S называются проецирующими лучами.
На начальном этапе необходимо изучить базовые положения. Перспективные масштабы (в т.ч. масштаб широт, масштаб высот, масштаб глубин). Дробная дистанционная точка, перспективная масштабная сетка. Необходимо показать связь основных законов геометрии с законы построения перспективы.
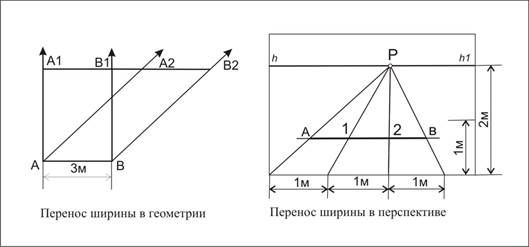
Масштаб широт.
Строят на прямых линиях, идущих параллельно основанию картинной плоскости. Этот метод основан на положении геометрии о параллельном переносе. Если нам надо перенести заданный отрезок на параллельную прямую, то для этого используются линии переноса, проведённые в любом направлении. Этот приём используют и в построении перспективы. На основании картинной плоскости строим отрезок натуральной величины и переносим его на заданную глубину при помощи линий переноса, которые направлены в точку схода, лежащую на линии горизонта.
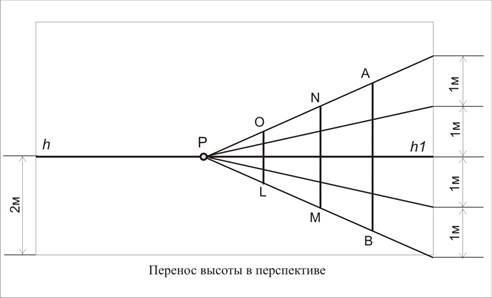
Масштаб высот.
Строят на горизонтальных прямых. В основе построения лежит положение геометрии о равенстве вертикальных отрезков, расположенных между параллельными прямыми. Это же положение применяют и при построениях перспективы. На одной из вертикальных прямых, принадлежащих картинной плоскости откладываем отрезок натуральной величины и переносим его, используя горизонтальные линии переноса, которые направлены в точку схода лежащей на линии горизонта.
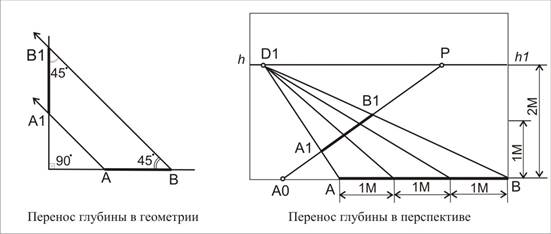
Масштаб глубин.
Строят на прямых, расположенных перпендикулярно картинной плоскости и идущих в центральную точку схода. Как и в предыдущих случаях в основе этого метода лежит
положение из геометрии. Если нужно перенести заданный отрезок на перпендикулярную к нему прямую, то для решения этой задачи, через его крайние точки проводят параллельные прямые, расположенные под углом в 45°. Образованный, таким образом, на перпендикулярной прямой отрезок будет равен заданному отрезку. Так как в результате ими образован равносторонний треугольник, у которого гипотенуза направлена под углом в 45°, катеты будут равны. Это же положение применимо и для построения перспективы. Если нам надо построить в перспективе отрезок заданной длины, мы сначала на картине задаём глубинную прямую. На ней будет строиться заданный отрезок. От начала глубинной прямой на основании картинной плоскости откладываем натуральную величину нашего отрезка. Для того чтобы перенести его на глубинную прямую, надо провести линию переноса под углом в 45° из его крайней точки. Мы уже отмечали, что все горизонтальные прямые, расположенные под углом 45°к основанию картины, имеют точкой схода D1- D2 (дистанционные точки). Следовательно, мы из намеченной точки проводим линию переноса в дистанционную точку ( В D1 или D2 ). Полученный отрезок будет равен заданному. Если к заданному отрезку надо прибавить ещё один отрезок, то для этого на основании картинной плоскости от крайней точки предыдущего отрезка, откладываем величину следующего. И уже из его крайней точки проводим линию переноса в дистанционную точку. И на глубинной прямой, она отметит величину следующего отрезка. Если отрезки одинаковы, то мы можем увидеть, как на глубинной прямой они уменьшаются при удалении от картинной плоскости.