Айнымалы периодикалық синусоидалды емес тоқтың орташа әсерлік мәні

Периодикалық тоқтың әсерлік мәні . 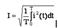(13.2)Периодты синусоидальды емес тоқты тригонометриялық қатарға саламыз 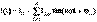және (13.2) кейіптемеге саламыз, түрлендіруден кейін мынаны аламыз 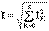. (13.3) Ұқсас кейіптемелер ЭҚК кернеулерінде де бар 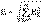, 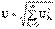.Периодты синусоидальды емес тоқтың тізбектеріндегі қуаты.Кернеу мен тоқтың лездік мәндерін тригонометриялық қатар түрінде жазайық

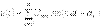
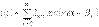Онда, актив қуат үшін былай жазуға болады

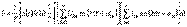(13.4)Интегралдағаннан кейін аламыз 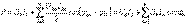(13.5)Осыдан, синусоидальды емес тоқтың актив қуаты актив қуаттардың бөлек гармоникалықтыларына тең болады 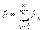.Осыған ұқсас реактив қуат үшін жазуға болады:

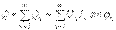.Толық қуат 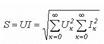.Синусоидалы емес ток үшін 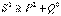Синусоидалы емес кернеу көзінің периодтық электр тізбектерін есептеСинусоидалы емес периодты қорек көзі бар сызықты электр тізбегін есептеу үш кезеңге бөлінеді:

а) Синусоидалы емес периодты функцияны тригонометриялық Фурье қатарына жіктеу (ЭҚК және ток көзі):

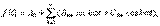мұндағы 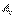–тұрақты құраушы немесе нөлдік гармоника;

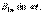
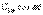–негізгі немесе бірінші гармоника;

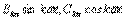
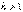_{болғандағы}–жоғарғы гармоникалар; 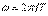–негізгі бұрыштық жиілік; – синусоидалы емес функцияның периоды.

б)Тізбектегі әр гармоникалық құраушы үшін бөлек – бөлек беттесу принципін қолдану, токтарды және кернеуді есептеу. Тізбектегі әр синусойдалы құраушыны есептеу үшін кешенді әдісті пайдалануға болады, бірақ әр түрлі синусоидалы құраушылар кешенді токтармен кернеуді қосуға болмайды. К ретті гармоника үшін индуктивті және сыйымдылықты кедергі мынаған тең.

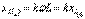
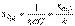,; (7.1)

в) Әр гармоникалық құраушы үшін алынған шешімді бірігіп қарастыру

24)Кешенді түрдегі Ом және Кирхгоф заңдары.Кешенді түрдегі Кирхгофтың заңдары.Кешенді түрдегі Кирхгофтың заңдары кешенді амплитуда және токтың, кернеудің, ЭҚК –нің кешенді мәндері үшін жазылады. Кирхгофтің бірінші заңы: Сұлбадығы түйіндердегі комплекстік токтың мәндерінің алгебралық қосындысы нөлге тең болып табылады: 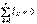Қарастырылып жатқан түйінге бағытталған болса, 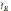тогы «+» таңбасымен жазылады. Ал «-» таңбасымен, берілген түйінге қарама-қарсы 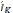тогы белгіленеді (немесе керісінше). Кирхгофтың екінші заңы:кешенді ЭҚК-нің барлық тұйықталған контурдағы кернеудің алгебралық қосындысы, сол контурдағы элементтердің кернеулерінің алгебралық қосындысына тең:

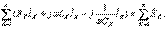
немесе Zk=Rk+j(Xlk-Xck) 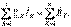Мұнда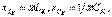

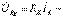активті элементтегі кешенді кернеу; 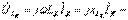индуктивтіліктегі кешенді кернеу; 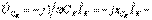сыйымдылықтағы кешенді кернеу; 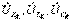керенеулері «+» таңбасымен жазылады, егер 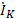тогы оң бағытталған және контурды айналған бағытпен сәйкес келсе. Ал «-» таңбасымен керісінше жағдайда жазылады. ЭҚК «+» таңбасымен жазылады, егер оң бағытталған және контурды айналған бағытпен сәйкес келсе. Ал «-» таңбасымен керісінше жағдайда жазылады.Кирхгофтың заңдарын кешенді түрде анықтайтын теңдеулер синусоидалды ток үшін: ,

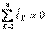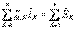
Сол сияқты тұрақты ток үшін:

, .

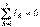
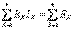Сондықтан, синусоидалды токты кешенді әдіспен есептеу толығымен тұрақты токтың есептеуіне ұқсайды. Тұрақты токты есептеуге қолданылатын барлық әдістер (КТӘ, ТПӘ, ЭГӘ т.б) сұлбадағы синусоидалды токты есептеуге болады, бірақ теңдеуде токтар мен кедергілер кешенді түрде шығады: 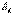, , 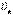, 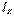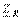. Мұндай тұрақты ток пен синусоидалды токты есептеу ұқсастығы, өзара индуктивтілік жоқ болғанда ғана болады. Кешенді түрдегі Ом заңының теңдеуі İ= Y Ů

25)Беттесу әдісі (Метод наложения). Егер электр тізбегіндегі берілген шамалар ЭҚК пен тоқ көзіндегі тоқтар болса, онда беттесу әдісі арқылы келесі жолмен тоқтардың мәндерін табуға болады. Кез келген тармақтағы тоқты ондағы орын алатын ЭҚК-нің әрбір тоқ көзінің жеке және осы тармақ арқылы әрбір тоқ көзінің әсерінен болатын тоқтың алгебралық қосындысы ретінде есептеуге болады. Тоқтардың мәндерін есептеген кезде мынаны ескеру қажет: кез келген тоқ көзінің ЭҚК-і немесе тоғы алынады да, сұлбадағы қалған тоқ көзінің ЭҚК-і қысқа тұйықталумен ауысады, ал тармақтар тоқ көзімен ажыратылады.

26) Индуктивті байланысқан элементтерді тізбектей қосуКедергілері 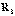, 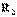индуктивтіктері 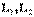бар екі индуктивті байланысқан катушка тізбектей қосылған. Қосылудың екі түрі бар: келісімді және қарсы.

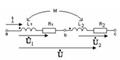10.2 Сурет Келісімді қосылу. Келісімді қосылған кезінде әрбір уақытта екі элементтердегі токтардың бағыттары аттас шықпаларға қарай бірдей(10.2,а суреті), сондықтан әрбір элементпен ілініскен өздік индукцияның магнит ағындары және өзара индукцияның магнит ағындары бір-бірімен қосылад 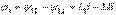, 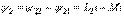.1 Келісімді қосылу кезінде екі тізбектеп қосылған индуктивтік байланысқан элементтердің индуктивтігі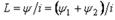

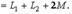
(10.8) Бірінші және екінші катушкадағы қыстырғыштардағы кернеудің кешендік түрі 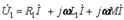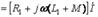, (10.9)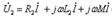 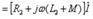. (10.10) Тізбектің қысқыштарындағы кернеу (10.2,а - сурет).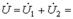 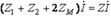(10.11) мұндағы 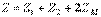- келісімді қосылу кезіндегі тізбектің кіріс кедергісі 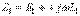; ; 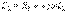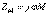. 10.3,а – суретте келісімді қосылудың векторлық сызбасы көрсетілген. Қарсы қосылу. Қарсы қосылғанда тізбектің екі элементтерінде әрбір уақытта аттас шықпаларға токтардың бағыттары қарама-қарсы (10.2,б сурет), сондықтан әрбір элементпен ілініскен өздік индукцияның және өзара индукцияның магнит ағындары бір-бірінен алынады. 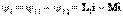, 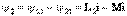. Қарсы қосылу кезінде екі тізбектеп қосылған индуктивтік байланысқан элементтердің индуктивтігі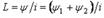

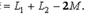
(10.12) Бірінші және екінші катушкадағы қыстырғыштардағы кернеудің комплекстік түрі 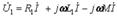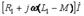(10.13)

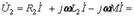
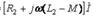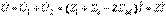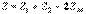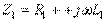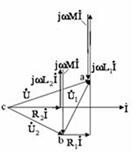
(10.14) Тізбектің қысқыштарындағы кернеу (10.2,б сурет) (10.15) мұндағы - қарсы қосылу кезіндегі тізбектің кіріс кедергісі. , 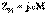.10.3,б – суретте келісімді қосылудың векторлық сызбасы көрсетілген ( 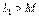және 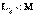кезінде).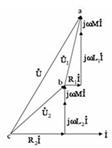

27)Кернеу резонансы. Кернеу резонансының қисықтары және жиіліктік сипаттамалары. Кернеу резонансы реактивті кіріс кедергі нолге тең болған кезде тізбектей жалғанған тербелмелі контурда (5.1 -сурет) пайда болады. 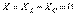немесе 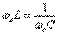(5.1) 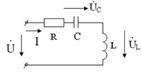5.1 Сурет

Резонанс кезіндегі тізбектегі максималды ток 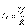. (5.2) Контур кедергісі – минималды 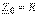. (5.3) Резонанс режимінде 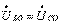Резонанс контурының төзімділігі: 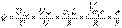, (5.4) мұндағы 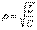- контурдың сипаттамалық кедергісі. Резонанстық жиілік: 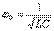немесе 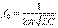. (5.5) Векторлық сызбалар (5.2-сурет): а) резонансқа дейін,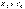 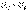болған кезде; в) резонанстан кейін,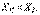 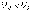болғанда; с) резонанс кезінде,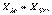 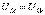болғанда.

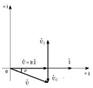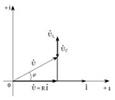а б 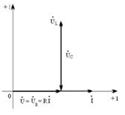в 5.2 Сурет. Контурдың жиілік сипаттамалары 5.3 –суретте көрсетілген:

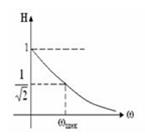
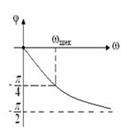
5.3 Сурет. Тізбектей жалғанған тербелмелі контурдың резонанстық қисықтары 5.4 –суретте көрсетілген.

5.4 Сурет

28. Потенциалдық сызба тұрақты тоқ тізбегін талдау үшін қарастырылады. Потенциалдық сызбаны салу үшін контурды немесе тізбектерді потенциалдар аймағына бөледі, сонымен қатар абсцисса осінде кедергілердің қосындысы, ал ординат осінде сәйкес нүктелердің потенциалдары орналасады. Сондықтан тізбектің немесе контурдың потенциалдық сызбасы әр аймақтағы нүктелерінің потенциалы бойынша салады.

Мысалы: 2.4 – суреттің сызбасын қарастырайық.

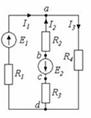2.4 Сурет 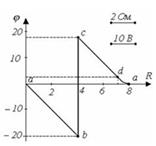2.5 Сурет Сұлбаның көрсеткіштері

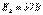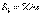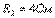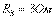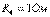; ; ; ; ; , , ал тармақтың тоқтары: 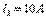; ; 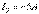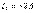. «аbcda» контуры үшін потенциалдық сызбасын саламыз. Алынған контур бойынша абсцисса осіне масштабпен кедергілердің қосындыларын аламыз: 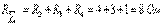, бұдан кейін әр нүктенің потенциалын, нөл етіп алынған «а» нүктенің потенциалы бойынша анықтаймыз ( 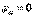). 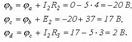Сол себептен, потенциалдық сызбаның координат нүктелері: а(0;0);b(4;-20); c(4;17); d(7;2). Нәтижесінде (2.5-сурет) алынған контурдың потенциалдық сызбасын масштаб бойынша саламыз.

29 Кешенді түрдегі түйіндік потенциалдар әдісіТүйіндік потенциалдар әдісіМысал. Түйіндік потенциалдар әдісі бойынша теңдеу құрамыз (7.3 – сурет)

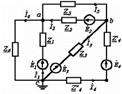7.3 Сурет «а» және «в» түйіндері үшін түйіндік потенциалдар әдісі бойынша теңдеу құрамыз. j_с=0: «с» түйіндегі потенциал нөлге тең

.

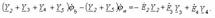
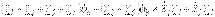Тармақтардағы тоқтарды Ом заңы арқылы өрнектейміз

31.Синусоидалды электр тізбектерінің шамалары және айнымалы токтың әсерлік мәндеріАйнымалы тоқ ұзақ уақыт бойы қолданыста болмады. Бұның себебі, алғашқы электр энергияның генераторы тек тұрақты өндіретін, бұл тұрақты тоқ электрохимиялық технологиялық процестерді ойдағыдай жақсы қанағаттандыратын, оның үстіне тұрақты тоққоздырғыштарды қолдануға өте ыңғайлы болды. Бірақ уақыт өте өндірістің дамуына байланысты тұрақты тоқ энергиясын қолдануына, үнемді электрмен қамтамасыз етуін қанағаттандырмады. Айнымалы тоқ трансформатор көмегімен электр энергияны нәтижелі қосуына және кернеу шамаларын өзгерту мүмкіндігін туғызды. Үлкен электрстанциялардан электр энергияны қолданушыларға үнемді жеткізуге мүмкіншіліктер туды, электрмен қамтамасыз ету кең етек жайды.

Қазіргі уақытта барлық орталық өндірістер мен электр энергия тек айнымалы тоқпен жұмыс істейді. Айнымалы тоқ тізбектері тұрақты тоқ тізбектерімен салыстырғанда артықшылықтары көп. Айнымалы тоқ пен кернеу өрісінің айналасында электр және магнит өрісін тудырады. Осы өрістерді өзгерту нәтижесінде тізбекте өздік индукция құбылысы пайда болады, ал бұл құбылыс тізбекте жүретін процестер үшін өте маңызды.

Барлық мүмкін болатын тоқтардың ішінде ең көп тарағаны синусоидалы тоқ. Синусоидалы тоқты басқа тоқтармен салыстарғанда электр энергияны үнемді өндіреді, жеткізеді және тасымалдайды. Тек синусоидалы тоқты қолдану арқылы күрделі сызықты тізбектегі барлық жердегі тоқтарды және қисық сызықты кернеу формаларын сақтап қалуға болады

Айнымалы тоқ (ЭҚК, кернеу және т.б) деп тоқтың (ЭҚК, кернеу және т.б) уақыт бойынша өзгеруін айтады. Электр тізбекте кернеудің және тоқтың шамалары тең уақыт аралық сайын қайталанатын процесс периодты деп, ал периодты шаманың мәні қайталанатын ең аз уақытты период деп атайды. Периодты тоқ үшін 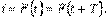Периодқа кері шама, яғни уақыт бірлікте периодтардың саны жиілік деп аталады. Жиіліктің өлшем бірлігі Герцпен (Гц) алынады 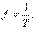Техникада қолданатын диапазон жиіліктері: ең төменгі жиіліктен (00,1 – 10 Гц, автоматты түрде жөнге келтіру жүйесінде, жергілікті есептеуіш техникасында), ең үлкен жиілікке дейін (3000 – 30000 МГц, миллиметрлік толқындар: (радиолокация, радиоастрономия). Өнеркәсіптік жиілік f = 50Гц.Айнымалы шаманың лездік мәні уақыт функциясы болып табылады. Оларды кіші әріптермен белгілейді: i – тоқтың лездік мәні i(t); u– кернеудің лездік мәні u(t); е – ЭҚК лездік мәні е(t); р – қуаттың лездік мәні р(t). Айнымалы шаманың бір периодтағы ең үлкен лездік мәнін амплитуда деп атайды (оны m индекісі бар бас әріппен белгілейді): I_m - тоқ амплитудасы; U_m - кернеу амплитудасы; E_m - ЭҚК амплитудасы.Тоқтың жылулық әсері және екі сымның олар арқылы бірдей тоқ өткенде өзара әсерлік механикалық күш тоқтың шамасына пропорционалды. Сондықтан, тоқтың мәнін период бойы әрекетті мәнімен белгіленеді 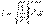(5.3) Сол сияқты ЭҚК пен кернеудің әсерлік мәндері де анықталады. (5.3) кейіптемесі бойынша синусоидалды тоқтың әсерлік мәнін жазамыз 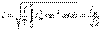. (5.4)Талдау нәтижесінде синусоидалды кернеу мен ЭҚК тапсақ болады. Осылай негізгі синусоидалды тоқтарды және ЭҚК пен кернеуді табамыз. ЭҚК және кернеу амплитудалық мәннен 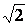есе кіші.

32.Өзара индуктивті байланыс элементтерін параллель қосу.Тізбектің екі катушкасы кедергілері 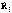, 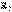индуктивтіктері 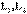параллель қосылған және де олардың аттас шықпалары бір түйінге қосылған (10.4 - сурет).

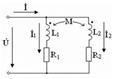Тізбек үшін Кирхгоф заңын жазамыз (10.4 - сурет) 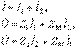(10.16) мұндағы 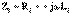, , 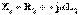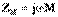. ( 10.16) теңдігін шешкенде, мынаны аламыз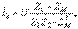 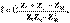(10.17) Тізбектің кіріс кедергісі 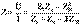. (10.18)

34/Айнымалы ток тізбегі үшін активті, реактивті және толық куаттарЭлектр тізбегі бойынша W энергиясының тас ымалдауын, энергияның таралуын (электромагниттік энергияның жылулық энергияға айналуы) және энергияның ауысуының басқа да түрлері процестің өту шапшаңдығымен сипатталады. Энергияның айналуы немесе тасымалдану шапшаңдығы қуат деп атайды 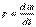Бір период кезіндегі лездік қуаттың орташа мәні активтік қуат деп аталады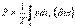 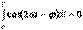екенін ескерте отырып 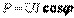екенін аламыз. Пассивтік екіполюстіктің пайдаланатын активтік қуаты теріс бола алмайды, (әйтпесе екіполюстік энергия өндіреді) сондықтан кірісінде 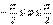жағдайы екіполюстік теория бойынша мүмкін, мұндағы екіполюстіктің актив кедергісі жоқ, тек идеал индуктивтік және сыйымдылығы бар.Резистор (идеал активті кедергі) 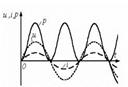8.2 Сурет Мұнда тоқ пен кернеудің фазалары бірдей (8.2 - сурет) 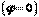, сондықтан оң, резистор актив қуатты пайдаланады 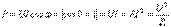Реактивті қуаттың өлшем бірлігі вольт – ампер реактивті (ВАр) болады. 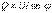. Электротехникада активті және реактивті қуаттардан бөлек толық қуат түсінігінде кеңінен қолданылады 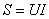[ВА] Активті, реактивті және толық қуаттар келесі теңдеу арқылы байланысады 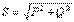Толық қуаттың активті қуатына қатынасы қуат коэффициенті деп атайды. Жоғарыда көрсетілген теңдеулерден, қуат еселеуіші 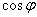тоқпен кернеу арасындағы ығысу бұрыш косинусына тең.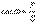

33 Эквивалентті генератор принципі.Эквивалентті генератор әдісіЭквивалентті генератор әдісін қолдану (активті екіұшты әдісі немесе бос жүріс және қысқа тұйықталу әдісі). Күрделі тізбектің кез келген тармағындағы тоқты анықтауға негізделген. Әдістің екі нұсқасы бар:1. Эквивалентті тоқ көзінің ЭҚК әдісі.2. Эквивалентті тоқ көзі әдісі.Эквивалентті тоқ көзінің ЭҚК әдісі. Кез келген «ав» тармақтағы I тоғын анықтау үшін, кедергісі R болатын (4.1, а - сурет; А әрпі активті екіполюсті білдіреді.) сол тармақты ажырату керек (4.1, б - сурет) осы тармаққа қосылған қалған тізбекті, эквивалентті тоқ көзінің ЭҚК Е_эк – мен, R_эк ішкі кедергісін ауыстыру керек. (4.1, в - сурет). Осы тоқ көзіндегі ЭҚК Е_эк, ажыратылған тармақтың қысқыштарындағы кернеуіне тең. (Бос жүріс кернеуі) 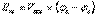. (4.1)Е_эк табу үшін, бос жүріс кезіндегі сұлбаның есептелуі, кез келген белгілі тәсілді қолданылады.Эквивалентті тоқ көзінің ЭҚК ішкі кедергісі R_эк бастапқы сұлбаның а және в қысқыштарына қатысты пассивті кіретін кедергіге тең, одан тоқ көздері ажыратылған (тоқ кезіндегі ЭҚК қысқа тұйықталу аумағымен ауыстырылған, ал тармақтар тоқ көзінен ажыратылған.(4.1, г - сурет; П әрпі тізбектің пассивтігін көрсетеді), «ав» тармағы ажыратылған кезде. R_эк кедергісін 4.1-суреттегі сұлба арқылы есептеуге болады. R кедергісі бар, ізделінетін сұлба (4.1, д - сурет) тармағының тоғы Ом заңы бойынша анықталады 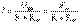.Эквивалентті тоқ көзі әдісі R кедергісі бар, ав тармақтағы тоқты есептеу үшін а және в қысқыштарына қатысты сұлбаның бір бөлігін эквивалентті тоқ көзімен ауыстыру керек, оның тоғы J_эк, ал өтімділігі G_эк (4.1,е - сурет)J_эк тоқты табу үшін, а және в қысқыштарын кез келген әдіспен I_қ тұйықталуы бар, қысқартылған аймақ бойымен өтетін тоқты есептеу керек. (4.1, ж - сурет). Сонымен J_эк= I_к. Эквивалентті тоқ көзі ЭҚК әдісі сияқты R кедергіні есептеуге болады. (4.1, г - суреттен). Сол кедергіні қысқа тұйықталу сұлбасының орын ауыстыру сұлбасында көрсетілгендей (4.1, з - сурет) кейіптеме бойынша есептелінеді. R_эк=Е_эк/I_k=Е_эк/J_эк=1/G_эк. (4.3)R тармақтағы тоқ (4.1 – сурет) 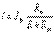(4.4) Эквивалентті генератор әдісін қолдануға мысал ретінде 4.2 – суреттегі амперметр көрсетуінің тәуелділігін анықтаймыз 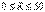Ом аралығындағы көпір диагоналындағы айнымалы резистордың R кедергінің өзгеруі кезінде.Тізбек көрсеткіштері: Е=100 В; R₁=R₄=40 Ом; R₂=R₃=40 Ом 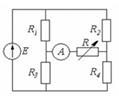4.2 Сурет 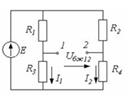4.3 Сурет мәнін табу үшін 4.3 – суреттегі сұлбаға ораламыз, ол жердегі кернеу 1-2 ашық қысқыштағы кернеу 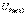ЭҚК пен анықталады. Берілген тізбекте 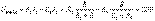Активті екіұшты кіріс кедергісін табу үшін оны 4.4 - суреттегі сұлбаға трансформерлейміз. 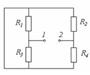4.4 Сурет 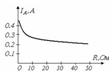4.5 Сурет Бұл пассивті екіұшты, 1-2 қысқыштың жағындағы кедергісі мынаған тең .Осы жағдайда, 4.2 суреттегі сұлбадағы амперметрді көрсету үшін (4.2) кейіптемеге сәйкес былай жазуға болады: 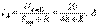. (4.5)R-дің өзгеру аралығына мән бере отырып, (4.2) кейіптемеге сәйкес 4.5 суреттегі қисық сызықты аламыз.

34. Айнымалы ток тізбегі үшін активті, реактивті және толық куаттар

Электр тізбегі бойынша W энергиясының тас ымалдауын, энергияның таралуын (электромагниттік энергияның жылулық энергияға айналуы) және энергияның ауысуының басқа да түрлері процестің өту шапшаңдығымен сипатталады. Энергияның айналуы немесе тасымалдану шапшаңдығы қуат деп атайды 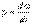Бір период кезіндегі лездік қуаттың орташа мәні активтік қуат деп аталады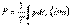 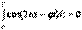екенін ескерте отырып 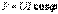екенін аламыз.

Пассивтік екіполюстіктің пайдаланатын активтік қуаты теріс бола алмайды, (әйтпесе екіполюстік энергия өндіреді) сондықтан кірісінде 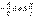жағдайы екіполюстік теория бойынша мүмкін, мұндағы екіполюстіктің актив кедергісі жоқ, тек идеал индуктивтік және сыйымдылығы бар. Резистор (идеал активті кедергі) 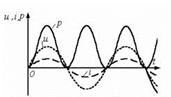8.2 Сурет Мұнда тоқ пен кернеудің фазалары бірдей (8.2 - сурет) 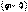, сондықтан оң, резистор актив қуатты пайдаланады 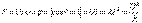Реактивті қуаттың өлшем бірлігі вольт – ампер реактивті (ВАр) болады. 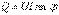. Электротехникада активті және реактивті қуаттардан бөлек толық қуат түсінігінде кеңінен қолданылады 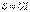[ВА] Активті, реактивті және толық қуаттар келесі теңдеу арқылы байланысады 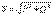Толық қуаттың активті қуатына қатынасы қуат коэффициенті деп атайды. Жоғарыда көрсетілген теңдеулерден, қуат еселеуіші 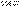тоқпен кернеу арасындағы ығысу бұрыш косинусына тең.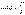

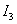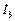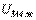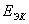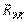35.Активті екіұштық әдісі (тұрақты ток тізбегі үшін).Эквивалентті генератор әдісі. тогынэквивалентті генератор әдісімен есептеп шығарамыз. тогы бар белгіленген тармақ қосылған тізбекті ажыратылған тармақтың қысқыштарындағы кернеуге тең эквивалентті ЭҚК-мен және кедергісімен ауыстырамыз (2.17 -суретті қараңыз). 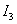тогын Ом заңымен табамыз: 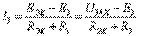(2.41)

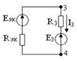2.17 Сурет 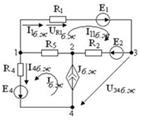2.18 Сурет 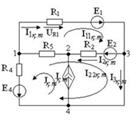2.19 Сурет Берілген сұлбадан (2.18 -сурет) R₃ кедергісі бар тармақты ажыратып, 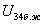-ті табамыз: 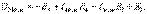Контурлық токтар әдісімен 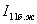-ті табамыз:

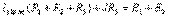(2.42) 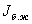тәуелді ток көзін контурлық ток арқылы өрнектейміз: 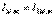болғандықтан,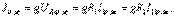 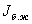-ті (2.42) теңдеуіне қойып, контурлық ток 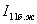-ті табамыз: 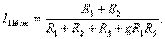(2.43)

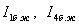токтары мынаған тең: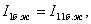

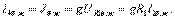
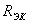кедергісін келесі формуламен табамыз: 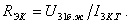(2.44) 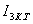тоғын контурлық токтар әдісімен табамыз (2.19 -суретті қараңыз): 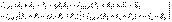(2.45Мұндағы тәуелді ток көзі 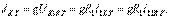(2.45) теңдеулер жүйесін шешіп, 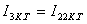-ті және 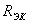-ны табамыз. 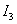тогын (2.41) кейіптемесімен есептейміз.Тоқтар резонансыДәріс мақсаты: параллель тербелмелі контурдағы резонанстың құбылысын зерттеу.

36 Параллель орналасқан контурдың резонансы

12.1 Тоқтар резонансы Параллель тербелмелі контурда тоқтар резонансы мына шартта пайда болады, егер реактивті өткізгіші кіріс болса 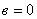; 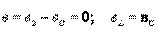. (12.1)

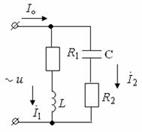
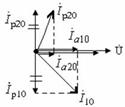
12.1 Сурет 12.2 Сурет(12.1) есепке ала отырып, толық өткізгіштің активті екенін анғаруға болады

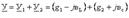
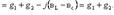(12.2)Тоқтар резонансы жалпы тоқта ең аз және кернеу кірісімен тең (12.2 -сурет)

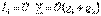(12.3)

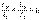. (11.4)

Беріктілік контуры

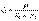(12.5)

мұндағы 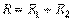-контурдың активті кедергісі;

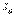- өткізу жолағы. 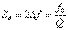. (12.6)

37 Параллель қосылған тоқ көзінің бір эквивалентпен ауыстыру әдісіЕгер бірнеше тоқ көзіндегі тоқтар J_1, J₂…J_n қосымша (3.2,а - сурет), онда оларды бір эквивалентті тоқ көзімен ауыстыруға болады (3.2,б - сурет) оның J_эк тоғы, тоқтардың алгебралық қосындысына тең, ал ішкі өтімділігі G_эк бөлек көздерінің ішкі өтімділіктерінің қосындысына тең 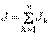; 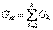. (3.10

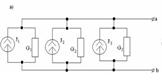
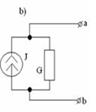3.2 Сурет

38.Эквивалентті генератор әдісі (айнымалы ток тізбегі үшін).

тоғын эквивалентті генератор әдісімен есептеу (ЭГӘ).

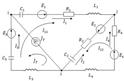Электр тізбегіндегі 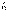тогымен қосылған тармақты эквивалентті ЭҚК 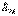көзімен, қысқыштағы тұйықталған 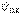бос жүрістегі кернеуге, және 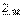кедергі, тогымен қосылған тармақтағы қысқыштарға қатысты пассивті электр тізбегінің кірісіндегі кедергіге тең алмастырамыз.(4.6-сурет) Барлық тәуелсіз кернеу көздері мен токтардағы ЭҚК нөлге теңестірілсе активті тізбек пассивті электр тізбегіне айналады. Сұлбадағы идеалді ЭҚК көзі қысқа тұйықталған бөлікпен алмастырылып, идеалды ток көзі тармақтан ажыратылады ( 4.8-сурет)

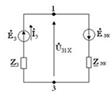4.6 Сурет 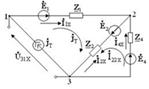4.7 Сурет

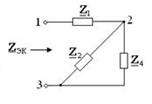4.8 Сурет 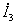тоғын Ом заңымен анықтаймыз:

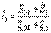(4.9 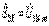табу үшін 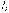тогы бар тармақты ажыратып, жаңа сұлбаны аламыз. (4.2.6-сурет). Сұлбадан (4.7-сурет ) 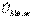кернеуін табамыз: 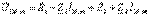(4.10) КТӘ бойынша 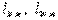есептейміз. Белгісіз 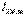контурлық тогын есептеу үшін теңдеулер жүйесін құрамыз (4.7-сурет): 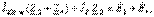(4.11) 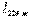тогын табайық: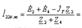

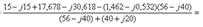
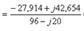
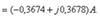
Токтарды табайық

: :

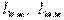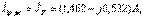
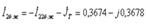
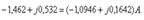
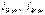токтарын (4.2.10)-теңдеуіне қойып, 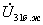анықтаймыз.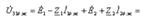

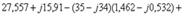
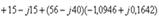
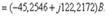
Электрлік тізбек арқылы 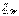анықтаймыз (4.8 –сурет):

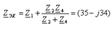
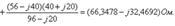
Табылған 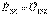және 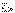мәндерін (4.9) теңдеуіне қойып, 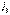тогын анықтаймыз.

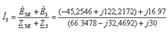
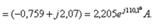
39 Қуаттар тепе – теңдігі Энергияның сақталу заңынан білетініміздей, берілген актив қуат жұмсалатын барлық актив қуаттарға тең 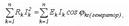Тепе – теңдік реактивті қуаттар үшін де сақталады 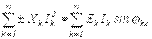(8.14) мұндағы «+» таңбасы индуктивті элементтерге қатысты ( 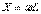) «–» – таңбасы сыйымдылыққа ( 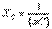) қатысты болады. (8.14) «j»–ға көбейтіп шыққан жауапты (8.13) – ке қойсақ, біз қуаттар тепе – теңдігінің синусоидалды тізбек тоғының аналитикалық түрін табамыз 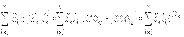Немесе 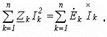(8.16)