Задачи по курсу «Теоретическая механика и теория поля» и их решение

1.Наити функцию Лагранжа двойного плоского маятника , находящегося в однородном поле тяжести (ускорение силы тяжести g).

Решение. в качестве координат берём углы φ₁ и φ₂, которые нити l₁ и l₂ образуют с вертикалью. Тогда для точки m₁ имеем:

чтобы найти кинетическую энергию второй точки, выражаем её декартовы координаты x₂, y₂ (начало координат в точке подвеса, ось y – по вертикали вниз) через углы φ₁ и φ₂:

после этого получим:

окончательно:

2.Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m₂, точка которого (с массой m₁ в ней) может совершать движения по горизонтальной прямой.

Решение. Вводя координату x точки m₁ и угол φ между нитью маятника и вертикалью, получим:

3. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

Решение. В декартовых координатах x, y, z:

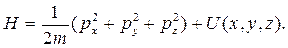
В цилиндрических координатах r, φ, z:

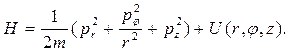
В сферических координатах r, θ, φ:

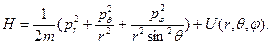
4. Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса 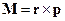материальной частицы.

Ответ: =-p_z

=0, =-p_y

5. Определить скобки Пуассона, составленные из компонент М.

Ответ: =-M_z, =-M_x , =-M_y.

6. Показать, что

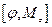=0, ,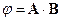

где φ – любая скалярная функция координат и импульса частицы.

Указание. Скалярная функция может зависеть от компонент векторов r и pтолько в комбинациях r²,p², . Поэтому

и аналогично для .

7. Показать, что

= ,

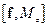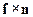где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.

Указание. Произвольный вектор f(r, p) может быть написан в виде где - скалярные функции

8. Выразить амплитуду и начальную фазу колебаний через начальные значения x₀, v₀ координаты и скорости.

Ответ:

9.Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.

Решение. Потенциальная энергия пружины (с точностью до малых величин высшего порядка) равна произведению силы F на удлинение δl пружины. при x<<l имеем:

,

так что U=Fx²/2l. Поскольку кинетическая энергия есть то

10. Найти частоту колебаний маятника, точка подвеса которого (с массой m₁ в ней) способна совершать движение в горизонтальном направлении.

Решение. При φ<<1 находим:

Отсюда

11. Определить малые колебания двойного плоского маятника.

Решение. Для малых колебаний 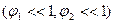найденная в задаче 1 параграфа 5 функция Лагранжа принимает вид :

.

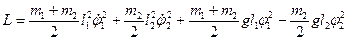Уравнения движения:

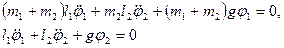
После подстановки (23,6) :

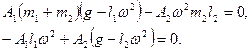
Корни характеристического уравнения:

Ответ: .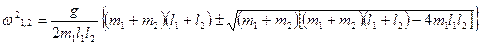

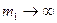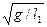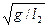При частоты стремятся к пределам и , соответствуют независимым колебаниям двух маятников.

12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

Решение.

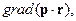
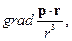
13. Вычислить 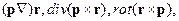где p – постоянный вектор.

Решение.

14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

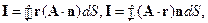
если объем, который охватывает замкнутая поверхность, равен V; A –постоянный вектор.

Решение. Умножим искомый интеграл на постоянный вектор р:

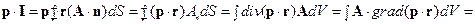
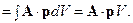
Так как вектор рпроизволен, то

.

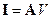Аналогично показывается, что

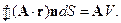
15. Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара . Объемная плотность заряда равна 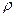, радиус шара R.

Решение. Из принципа суперпозиции полей следует, что искомая напряженность поля равна разности напряженности электрического поля, создаваемого шаром без полости, и напряженности поля зарядов, заполняющих при этом полость.

Поле внутри полости

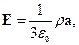
поле внутри шара (но вне полости)

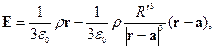
поле снаружи шара

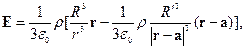
где 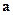- радиус-вектор, проведенный из центра шара к центру полости.

16. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

Решение. Потенциал точечного заряда является решением уравнения

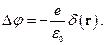(1)

Представим 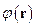и 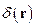в виде разложений в интеграл Фурье:

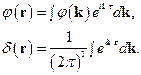(2)

Подставляя соотношения (2) в уравнение (1) и приравнивая в подынтегральных выражениях коэффициенты при 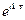, получим

.

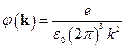17. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону: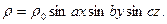

Решение. .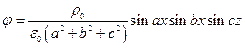

18. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

Решение. Предположив, что заряд расположен в начале координат, решим уравнения

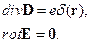
Направим оси декартовой системы координат по главным осям тензора диэлектрической проницаемости. Тогда

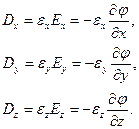
Подставим соотношения (2) в уравнение (1):

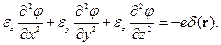
Заменой 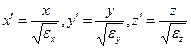уравнение приводится к виду

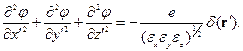
Здесь использовано свойство δ-функции:

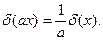
Решение уравнения (4) имеет вид

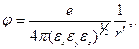
где

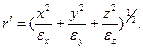
Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностьюj.Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

Решение. H=1/2

20. Показать, что постоянное однородное магнитное поле В можно описывать векторным потенциалом А= .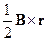

21. Найти интенсивность излучения частицы массы m,движущейся по круговой орбите радиуса а,под действием кулоновских сил. Выразить ответ через энергию частицы.

Решение. Из формулы, по которой вычисляется интенсивность дипольного излучения, где p=er, исключаем r, пользуясь уравнением движения

Отсюда

где Е – энергия частицы.

Экзаменационные вопросы по курсу «Теоретическая механика и теория поля».

1. Обобщенные координаты.

2. Описание эволюции системы в конфигурационном пространстве.

3. Принцип наименьшего действия в классической механике.

4. Уравнения движения Лагранжа.

5. Функция Лагранжа и ее свойства.

6. Функция Лагранжа простейших систем.

7. Интегралы движения (метод Лагранжа).

8. Преобразование Галилея.

9. Свойства симметрии пространства и времени.

10. Законы сохранения.

11. С и l системы

12. Циклические координаты.

13. Задача двух тел и сведение ее к эквивалентной одномерной.

14. Особенности движения частицы в центральном поле.

15. График эквивалентного одномерного потенциала.

16. Обобщенный импульс.

17. Малые колебания.

18. Свойства потенциальной энергии.

19. Колебания системы с одной степенью свободы.

20. Характеристическое уравнение.

21. Колебания системы с n-степенями свободы.

22. Дисперсионное уравнение.

23. Нормальные координаты.

24. Затухающие одномерные колебания.

25. Преобразование Лежандра и уравнения движения Гамильтона.

26. Динамические переменные в методах Лагранжа и Гамильтона.

27. Канонические сопряженные величины.

28. Описание эволюции системы в фазовом пространстве.

29. Функция Гамильтона и ее свойства.

30. Функции Гамильтона простейших систем.

31. Интегралы движения (метод Гамильтона).

32. Скобки Пуассона и их свойства.

33. Элементы тензорного анализа в классической механике.

34. Оператор .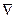

35. Уравнения Максвелла для электромагнитного поля в вакууме.

36. Потенциалы электромагнитного поля в вакууме.

37. Градиентная инвариантность.

38. -функция.

39. Закон сохранения заряда.

40. Объемная плотность точечного заряда.

41. Типы калибровок: Лоренца, Кулона, поперечных волн.

42. Уравнения Даламбера для потенциалов электромагнитного поля в вакууме.

43. Уравнения Максвелла для электромагнитного поля в среде без пространственно-временной дисперсии.

44. Потенциалы электромагнитного поля в среде.

45. Функциональные соотношения D=D(E), B=B(H), j=j(E) без учета пространственно-временной дисперсии.

46. Условия на границе раздела двух сред.

47. Нелинейные, неоднородные и анизотропные среды.

48. Уравнения Максвелла для стационарного электромагнитного поля в среде.

49. Тензоры 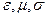и их свойства.

50. Функция Грина уравнения Гельмгольца.

51. Функция Грина уравнения Пуассона.

52. Некоторые задачи электростатики.

53. Некоторые задачи магнитостатики.

54. Приближение линейного тока.

55. Уравнения Максвелла для квазистационарного электромагнитного поля .

56. Условие квазистационарности поля и глубина его проникновения.

57. Уравнения Максвелла для электромагнитных волн в вакууме.

58. Волновое уравнение.

59. Фаза.

60. Фронт волны.

61. Фазовая скорость.

62. Решение волнового уравнения в случае плоской волны.

63. Плоская монохроматическая волна.

64. Калибровка Лоренца в случае однородной изотропной среды.

Задачи по курсу «Теоретическая механика и теория поля» и их решение (от А.Е.Широкова)

1.Написать функцию Лагранжа для циклоидального маятника и показать, что его период колебаний не зависит от амплитуды колебаний, в отличие от обычного математического маятника.

Циклоидальный маятник был изобретен Христианом Гюйгенсом, крупным ученым XVII столетия и гениальнейшим часовым мастером всех времен. Этот маятник свободен от недостатка, присущего обычному математическому маятнику неполного изохронизма (в общем случае период колебаний математического маятника зависит от амплитуды колебаний), благодаря тому, что в этом случае материальная точка движется не по дуге окружности, а по дуге циклоиды. Это мы покажем ниже.

Рис.1 Качение колеса с постоянной угловой скоростью образует обыкновенную циклоиду. Циклоиду описывает точка, лежащая на краю колеса. Угол качения – φ.

Решение. Напишем сначала уравнение циклоиды. Из рисунка видно, что уравнение циклоиды имеет вид:

(1)

Параметр φ означает угол, на который повернулось от своего исходного положения колесо радиуса а, катящееся по горизонтальной оси х. В случае обычной циклоиды точка, описывающая циклоиду, находится на окружности колеса. Но для нашего маятника нам нужна циклоида, острия (точки возврата) которой обращены не вниз, как на рисунке 1, а вверх (рис. 2) и которая образуется при качении колеса по нижней стороне оси х. Ее абсцисса x выражается по-прежнему уравнением (1), а выражение для ординаты y изменится:

Рис. 2 Циклоидальный маятник Гюйгенса для осуществления изохронизма. Использовано свойство циклоиды: эволюта циклоиды также является циклоидой. Таким образом, если в точке O на рисунке, где соприкасаются 2 верхние дуги циклоиды, закрепить нить длиной l=4a, и натянуть её так, чтобы она легла на левую или на правую ветвь циклоиды, то конечная точка m нити опишет нижнюю дугу циклоиды.

(2)

Далее напишем функцию Лагранжа для нашего маятника. Имеем:

Отсюда получаем:

(3)

Для дальнейшего анализа маятника выпишем уравнения Лагранжа для полученной нами в (3) функции Лагранжа:

Таким образом, дифференциальное уравнение циклоидального маятника запишется в виде:

После введения половинного угла и сокращения на :

(4)

Таким образом, уравнение (4) совпадает с уравнением малых колебаний математического маятника, для которого выполняется изохронизм. Для этого достаточно просто ввести новую обобщённую координату . Заметим, что уравнение (4) записано для общего случая, оно справедливо даже в случае больших отклонений маятника, то есть для циклоидального маятника доказан точный изохронизм.

2.Движение стержня, по которому ползёт насекомое. Концы прямолинейного однородного твёрдого стержня массы m и длины 2а скользят по гладкой горизонтальной окружности радиуса c. Вдоль стержня ползет насекомое, масса которого равна массе стержня, с некоторой постоянной относительной скоростью v. Написать функцию Лагранжа, уравнения Лагранжа. Получить решение уравнений Лагранжа.

Решение. К моменту времени t стержень образует с некоторым постоянным направлением на плоскости угол φ, а насекомое отползает от середины стержня на отрезок х. Вычислим сначала кинетическую энергию стержня. Разделим стержень на бесконечно малые элементы длины dx и просуммирует соответствующие им кинетические энергии. Результат даст полную кинетическую энергию стержня. Поскольку в момент времени t модуль скорости всех точек на стержне равен (стержень твёрдый), где , y – текущая координата на стержне, условимся её отсчитывать без ограничения общности от середины стержня, то кинетическая энергия всего стержня равна:

(1)

Кинетическая энергия насекомого складывается из скорости в направлении стержня и скорости в перпендикулярном к нему направлении, x=vt (начало отсчёта в середине стержня). Отсюда общая кинетическая энергия насекомого и стержня равна

(2)

Потенциальная энергия системы из условия задачи равна нулю. Тогда . Из (2) видно, что φ– циклическая переменная. В этом случае уравнение Лагранжа для единственной в нашем случае обобщённой координаты φ, как известно, упрощаются:

Отсюда

,

Что даёт нам следующее:

(3)

Решая (3), получаем ответ:

.

3. Качение диска по окружности другого вращающегося диска. В вертикальной плоскости находятся два одинаковых круглых диска радиуса а и массы М. Края дисков обладают абсолютной шероховатостью и поддерживаются в постоянном соприкосновении однородной штангой массы m и длины 2а, соединяющей их центры. Один из центров закреплен неподвижно, а соответствующий диск А вращается с постоянным угловым ускорением а. Определить движение соединяющей штанги и второго диска В.

Решение. К моменту времени t штанга образует с направленной вниз вертикалью угол , а диск А поворачивается на угол . Угловая скорость диска А равна , а скорость точки соприкасания дисков равна . Так как центр диска В имеет скорость , то угловая скорость вращения диска В вокруг своего центра равна . Каждый из дисков имеет относительно своего центра момент инерции, равный . Поэтому кинетическая энергия всей системы равна:

(1)

и

, - константа.

Для потенциальной энергии (начало отсчёта берём в центре диска A):

Тогда

Записываем уравнения Лагранжа (учитываем, что из условия задачи):

(2)

Домножаем обе части (2) на и интегрируем:

(3)

Уравнение (3) представляет собой уравнение с разделяющимися переменными, решение которого не представляет никаких трудностей.

4.Написать функцию Лагранжа для бусинки массы m, движущейся по вертикальной окружности радиуса r, вращающейся со скоростью ωвокруг вертикальной оси, проходящей через центр окружности.

Решение. Пусть x, y, z – декартовы координаты с началом в центре вышеупомянутой окружности и вертикальной осью z (ось z направлена вверх, ускорение свободного падения g – вниз). Пусть φ – угол плоскости окружности с плоскостью (x, z), q – угол, образованный радиус-вектором, проведённым из центра окружности к бусинке и осью z . Из условия задачи φ=ωt.

,

,

Таким образом, функция Лагранжа оказалась такой же, как в одномерной системе с кинетической энергией

,

И с потенциальной энергией

Здесь q выступает в роли обобщённой координаты.

5.Кольцо массы m скользит по однородному стержню длины 2а и массы М, вращающемуся в вертикальной плоскости вокруг одного из своих концов.

Решение. Пусть - полярные координаты кольца в момент времени t относительно конца стержня и горизонтали, причём угол отсчитывается вниз. Тогда функция Лагранжа системы записывается так (ось z направим вверх, ускорение свободного падения направлено вниз):

В результате

6.Движение стержня во вращающейся раме. Концы однородного тяжелого стержня массы M скользят без трения по горизонтальному и вертикальному брусьям некоторой рамы, вращающейся с постоянной угловой скоростью ω вокруг вертикального бруса. Написать функцию Лагранжа для стержня.

Решение. Пусть 2a — длина стержня, М — его масса, — угол, который он образует с вертикалью. Имеем:

и - составляющие кинетической энергии, соответствующие движению стержня в плоскости рамы и вращению вокруг вертикального бруса рамы. Первая составляющая находится аналогично кинетической энергии стержня из задачи 2. В нашем случае она равна:

Что же касается второй составляющей кинетической энергии, то нетрудно сообразить, что она равна

Потенциальная энергия стержня (отсчитываем от нижнего бруса рамы)

В итоге получаем:

7.Стержень скользит своими концами по гладкому круговому обручу. Обруч расположен вертикально и вращается вокруг своего вертикального диаметра. Масса стержня равна m, его длина 2a; масса обруча равна М и его радиус r.

Решение. В момент времени t стержень образует с горизонталью угол , а обруч имеет по отношению к некоторой неизменной вертикальной плоскости азимут . Момент инерции стержня по отношению к оси, проходящей через центр обруча перпендикулярно к его плоскости, равен (см. задачу 2 из этого параграфа). Момент инерции стержня относительно вертикального диаметра обруча равен:

Отсюда кинетическая энергия системы

При этом потенциальная энергия системы (начало отсчёта в центре обруча, ось z направлена вверх).

В итоге

8.Получить условие падения частицы на центр в центральном поле.

Решение. В случае центрального поля полная энергия частицы имеет следующий вид:

(1)

В (1) m – масса частицы, M – момент импульса частицы (сохраняется при движении в центральном поле), U(r) – потенциальная энергия частицы. Из (1) следует очевидное неравенство:

(2)

Из (2) получается следующее:

(3)

Из (3), в свою очередь, получаем, что r может принимать стремящиеся к нулю значения лишь при условии

(4)

Из (4) следует, что U(r) должно стремиться к минус бесконечности либо как с , либо пропорционально .

9.Проинтегрировать уравнения движения задачи двух тел из предыдущего параграфа.

Решение. Выше мы получили функцию Лагранжа для системы двух тел:

(1)

В (1) -приведённая масса, , - координата центра масс системы, M- момент импульса системы, который в данном случае сохраняется:

(2)

Таким образом, задача сводится к двум задачам: задаче свободного тела с массой m₁+m₂ (движения центра масс) и задаче одномерного движения с эффективным потенциалом . Поскольку движение центра масс в данном случае тривиально, то нас будет интересовать вторая задача с . Можно напрямую выписать уравнение Лагранжа для L₂ и решить его, однако в данной задаче существуют интегралы движения, которые позволяют существенно упростить процедуру решения. Помимо вышеупомянутого момента импульса в задаче сохраняется также энергия системы, поскольку функция Лагранжа (1) не зависит явно от времени:

(3)

Фактически (3) – уравнение с разделяющимися переменными (E=const). Решив (3), можно получить неявную связь r и t:

Вспомним про связь (2), которая позволяет связать φ с r. В итоге получаем:

(4)

При этом допустимая область движения определяется из условия неотрицательности подкоренного выражения.

10.Нарисовать фазовый портрет (фазовые траектории) для частицы, движущейся в одномерном потенциале, приведённом на рисунке.

Решение. Фазовым пространством системы с n степенями свободы называется 2n-мерное пространство обобщённых координат и импульсов. Каждая точка в нём отвечает определённому состоянию системы. Совокупность точек, изображающих состояния системы в различные моменты времени, образует в фазовом пространстве некоторую кривую. Ее называют фазовой траекторией системы. Поскольку, по самому смыслу понятия состояние, задание состояния системы в некоторый момент t = t₀ предопределяет её состояния во все другие моменты времени, то задание изображающей точки в некоторый момент t = t₀ предопределяет всю фазовую траекторию (в отличие от задания положения системы в конфигурационном пространстве, оставляющего широкий простор для возможных конфигурационных траекторий). Таким образом, через каждую точку фазового пространства проходит только одна фазовая траектория. Закон сохранения энергии позволяет легко находить фазовые траектории. Действительно, на каждой фазовой кривой значение полной энергии постоянно. Поэтому фазовые кривые удобно строить, как множества уровней энергии . Фазовые траектории также можно качественно нарисовать, имея перед собой график потенциальной энергии.

При исследовании уровней энергии следует обращать внимание на критические значения энергии (те, которые соответствуют локальным минимумам и максимумам потенциальной энергии). При этом возможны некие механические аналогии, например, сопоставление с шариком, катающимся в потенциальной яме, соответствующей потенциальной энергии нашей системы. Так, рассуждение ”Кинетическая энергия неотрицательна. Чем потенциальная энергия меньше, тем скорость больше” принимает на этом языке вид:”Шарик не может выскочить из потенциальной ямы, поднявшись выше уровня, определяемого его начальной энергией. Скатываясь в яму, шарик набирает скорость”. Фазовый портрет системы с потенциальной энергией, изображённой на вышеприведённом рисунке, приведён ниже.

11.Найти период малых колебаний бусинки массы 1 на проволоке y=U(x) в поле тяжести с g=1 вблизи положения равновесия x=x₀.

Решение. Начало отсчёта введём в точке равновесия x=x_0. Ось y направим вертикально вверх (ускорение свободного падения направлено вниз). Имеем

(1)

В силу того, что x=x₀-положение равновесия . Отсюда получаем, что частота колебаний определяется формулой:

(2)

При этом для линеаризованной системы получаем .

12.Исследовать собственные колебания двух разных маятников (m₁, m₂, l₁, l₂,g=1-ускорение свободного падения принимаем за единицу), соединённых пружиной с потенциальной энергией 1/2α(q₁-q₂)². Получить асимптотические выражения для собственных частот в пределе при α->∞ и α->0.

Решение. Имеем следующие выражения для кинетической и потенциальной энергии:

(1)

В силу этого, матрицы, отвечающие квадратичным формам кинетической и потенциальной энергии таковы:

(2)

Тогда характеристическое уравнение имеет вид (λ=ω²):

,

или

(3)

Где

Из (3) видно, что при (очень сильная пружина) одна из частот стремится к бесконечности, а другая - к собственной частоте маятника из двух масс на одном стержне:

13.Найти распределение электрического поля между двумя бесконечными заземлёнными пластинами конденсатора, между которыми параллельно ним расположена равномерно заряжённая нить с линейной плотностью заряда q (см. рисунок), проходящая через точку (0,d). Ось z параллельна пластинам.

Решение. Имеем дело с электростатикой. Нам необходимо решить основное уравнение электростатики

(1)

в пространстве между пластинами, где - скалярный потенциал электромагнитного поля, . При этом должны соблюдаться следующие граничные условия (равенство нулю потенциала на заземлённых пластинах и обращение в нуль потенциала на бесконечности):

(1.1)

В силу симметрии задачи удобно воспользоваться методом разделения переменных. Вообще говоря, если граничная поверхность соответствует постоянному значению одной из координат, то с граничными условиями очень удобно оперировать, будь то непрерывность потенциала или его производных, или постоянство этих величин. Это справедливо при любой системе координат. Однако при специально выбранных координатах мы можем пойти несколько дальше и записать решение в виде произведения функций отдельных координат. Тогда граничные условия нужно будет применять к функциям одной переменной. Так, в частности, обстоит дело в нашем случае.

Так, в нашем случае в силу симметрии задачи (пластины бесконечны, при этом , где - линейная плотность заряда нити), поэтому задача (1) двумерна

(2)

и прямоугольные координаты очень удобны для её решения. Во всех точках между пластинами конденсатора, кроме (0,d), уравнение (2) можно записать так:

(3).

Будем искать решение уравнения (3) в виде , где X и Y-функции только одного аргумента (x и y соответственно). В данном случае именно такой выбор решения и реализует вышеуказанную схему разделения переменных. Тогда, разделив (3) на , получим:

(4)

В последнем уравнении штрихи обозначают дифференцирование по соответствующей координате. Так как переменные x и y независимы, то оба члена в уравнении (4) не должны зависеть ни от одной из переменных. Следовательно, можно написать

(5)

Константа C называется параметром разделения. Если нет никаких ограничений на величину C, то произведение общих решений обыкновенных дифференциальных уравнений будет общим решением двумерного уравнения Лапласа. Однако граничные условия накладывают ограничения как на характер возможных решений, так и на величину параметра разделения. Решение мы выразим в виде суммы (или интеграла в зависимости от того, являются ли допустимые значения параметра разделения дискретными или непрерывными) допустимых частных решений с такими коэффициентами, чтобы удовлетворить граничным условиям. Для отыскания этих коэффициентов нужно использовать известное свойство ортогональности решений уравнения Лапласа.

Теперь нужно выбрать тот или иной знак параметра разделения. Предположим сначала, что параметр С в уравнении (5) положителен, С =k². Тогда соответствующие обыкновенные дифференциальные уравнения принимают следующий вид:

(6)

Их общими решениями являются функции

(7)

Эти решения должны удовлетворять граничному условию (1.1). Для того чтобы потенциал на пластинах равнялся нулю, достаточно положить, что , а , где n - целое число. Условия в бесконечности на оси х не удовлетворяются ни одним из членов функции X(x). Поэтому для положительных и отрицательных значений x нужно написать отдельные решения (таким образом, область между пластинами конденсатора делится на 2 части):

(8)

Так как потенциал φ непрерывен при x=0 (φ(+0,y)=φ(-0,y), это проверяется непосредственным интегрированием уравнения (1) по x вблизи x=0 2 раза), то коэффициенты соответствующих членов в обоих рядах равны, т. е. С_n=A_n. Если мы проинтегрируем (1) всего 1 раз по переменной x вблизи x=0, то получим условие, определяющее С_n=A_n однозначно:

(9)

Домножая (9) на и интегрируя по y в пределах от 0 до a, получаем выражение для (при этом используем известное свойство дельта-функции):

(10)

Таким образом, полное решение задачи имеет следующий вид:

(11)

Следует отметить, что выражение для того же потенциала выглядело бы совсем иначе, если выбрать другой знак у параметра разделения в соотношении (5). Пусть С=-k², тогда X(x) просто coskx, так как Х(х)—четная функция переменной х в силу симметрии задачи. Никаких ограничений на величину k не накладывается. Ввиду того, что нельзя подобрать единую функцию Y так, чтобы она обращалась в нуль на обеих пластинах конденсатора, рассматриваемую область следует опять разбить на две части, теперь уже плоскостью y=d. Аналогичные выкладки приводят к следующему выражению для потенциала:

(12)

Естественно, в силу теоремы единственности представления (11) и (12) эквивалентны, то есть описывают один и тот же потенциал.

14.Определить магнитное поле H в бесконечной цилиндрической полости, вырезанной в бесконечно длинном цилиндрическом проводнике. Радиусы полости и проводника соответственно a и b, расстояние между их параллельными осями d (b>a+d). Текущий в проводнике постоянный ток I равномерно распределён по сечению.

Решение. Имеем дело с магнитостатикой. Запишем уравнение для магнитного поля в интегральной форме и воспользуемся теоремой Стокса:

(1).

Далее, воспользуемся принципом суперпозиции полей. Результирующее поле в полости складывается из двух полей: поля H₁ проводника без полости и поля H₂, создаваемого током, текущим в полости с той же самой плотностью тока, только с противоположным знаком, таким образом, что результирующий ток в полости равен нулю (H=H₁+H₂). Эти поля мы найдём, воспользовавшись симметрией задачи и теоремой Стокса. В силу симметрии поля H₁ иH₂ в точках с радиус-векторами r₁ и r₂, проведёнными соответственно из центра проводника и центра полости, направлены по касательным к соответствующим окружностям. Тогда теорема Стокса даёт:

В результате получаем для результирующего поля H:

,

Причём направлено оно перпендикулярно плоскости, проходящеё через оси проводника и полости.

15. Внутри тонкой проводящей цилиндрической оболочки радиуса b находится коаксиальный с ней провод радиуса a. По проводникам текут токи одинаковой величины I в противоположных направлениях. Определить магнитное поле H, создаваемое такой системой во всём пространстве.

Решение. Как и в предыдущей задаче, воспользуемся теоремой Стокса. В качестве контуров циркуляции выберем окружности с центром в середине провода, поскольку в силу симметрии задачи магнитное поле будет направлено к ним по касательным.

1)r<a

2πrH=4π/c I (r²/a²),

H(r)=(2/c) I (r/a²)

2)b>r>a

2πrH=4π/c I,

H(r)=(2/c) I/r

3)r>b

2πrH=4π/c (I-I)=0.

Итак,