Определение бесконечно большой функции

Определение числовой функции. Способы задания функций.

Пусть D – множество на числовой прямой R. Если каждому х принадлежащему D поставлено в соответствие единственное число y=f(x), то говорят, что задана функция f.

Способы задания функций:

1) табличный – для функций, заданных на конечном множестве.

2) аналитический

3) графический

2 и 3 – для функций, определенных на бесконечном множестве.

Понятие обратной функции.

Если функция y=f(x) такова, что разным значениям х аргумента соответствуют разные значения у функции, то переменную х можно выразить как функцию переменной у: x=g(y). Функцию g называют обратной к f и обозначают f^(-1).

Понятие сложной функции.

Сложная функция- функция, аргументом которой является другая любая функция.

Пусть даны функции f(x) и g(x). Составим из них две сложные функции. Считая функцию f внешней (главной), а функцию g – внутренней, получаем сложную функцию u(x)=f(g(x)).

Определение предела последовательности.

Число а называется пределом последовательности {xn}, если для любого положительного существует номер n0, начиная с которого все члены посл-ти отличаются от а по модулю меньше, чем на ε (т.е. попадают в ε-окрестность точки а):

Правила вычисления пределов сходящихся последовательностей.

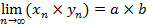1.Всякая сходящаяся последовательность имеет только один предел. 2. Если все элементы последовательности {x_n} равны С (постоянной), то предел последовательности {x_n}, тоже равен С. 3. ; 4. ; 5. .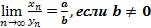

Определение ограниченной последовательности.

Посл-ть {x_n} называется ограниченной, если множество чисел X={x_n} ограниченно: .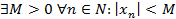

Определение бесконечно малой последовательности.

Посл-ть {x_n} наз-ют бесконечно малой, если для любого (сколь угодно малого) 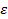>0 найдется такой номер n₀, что для всякого n>n₀ выполняется нерав-во |x_n|< .

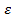Определение бесконечно большой последовательности.

Посл-ть наз-ют бесконечно большой, если для любого (сколь угодно большого) числа А>0 найдется такой номер n₀, что для всякого номера n>n₀ выполняется нерав-во |x_n|>A.

Определение монотонных последовательностей.

Монотонные посл-ти:1) возрастающая, еслиx_n<x_n+1 для всех n, 2) неубывающая, еслиx_n 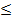x_n+1 для всех n, 3) убывающей, еслиx_n>x_n+1 для всех n, 4) невозрастающей, еслиx_n 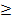x_n+1 для всех n.

Определение предела функции в точке.

Пределом ф-ии y=f(x) в точке x₀ (или при x 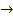x₀) наз-ют число а, если для любой посл-ти{x_n} значений аргумента, сходящейся к х₀ (при этом все x_n 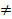x₀), посл-ть {f(x_n)} значений ф-ии сходится к пределу а.

Определение бесконечно малой функции.

Ф-ияf(x) наз-ся бесконечно малой при х→А, если .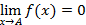

Определение бесконечно большой функции.

Ф-ияf(x) наз-ся бесконечно большой при х→А, если 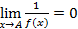.