Математическая модель неуправляемого авиационного средства поражения
Как было сказано выше определение параметров движения НАСП осуществляется на основе решения задачи внешней баллистики.
Баллистика – наука о движении тел относительно воздуха – одна из старейших наук. Второй закон механики Ньютона и следствия из него определяют параметры траектории АСП. Поэтому баллистику можно рассматривать как прикладную механику тел, перемещающихся под действием трех сил: аэродинамической, гравитационной и реактивной.
Внешняя баллистика – наука о движении неуправляемых тел относительно воздуха после прекращения их силового взаимодействия с пусковой установкой [11]. Тело, которому сообщена некоторая начальная скорость, совершает в пространстве свободное движение, т.е. движение, не ограниченное никакими механическими связями. Следовательно, внешняя баллистика имеет дело с движением твердого тела, обладающего шестью степенями свободы.
Рассмотрим решение задачи внешней баллистики НАСП, отделяемого от БАК, которое состоит в определении элементов траектории НАСП в условиях быстроизменяющейся воздушной обстановки. Под элементами траектории НАСП понимаются характеристики, описывающие его положение в любой точке траектории: скорость, ускорение, координаты центра масс, время полета и т.д.
Для решения задачи прицеливания используются основные элементы траектории НАСП: относ A, время падения T, и вспомогательные элементы траектории: скорость Vc и угол θc встречи.
В общем случае движение НАСП описывается 12 дифференциальными нелинейными уравнениями. Шесть из них определяют движение центра масс, шесть других – движение относительно центра масс. Интегрирование системы 12 дифференциальных уравнений составляет общую задачу внешней баллистики. В ряде случаев бывает достаточным определение движения центра масс без учета движения относительно центра масс при условии устойчивости АСП на траектории. Решение такой задачи называется основной задачей внешней баллистики. При этом полагается, что стабилизация НАСП осуществляется при помощи специальных стабилизаторов или приданием ему вращательного движения вокруг оси симметрии.
Главным преимуществом решения основной задачи внешней баллистики по сравнению с решением общей задачи внешней баллистики (при вычислении баллистических элементов) являются [12]:
- сравнительно небольшой объем вычислений на борту ЛА;
- малый объем первичной информации, вводимой в вычислительную систему КБО (вводится одна функция и одно число, характеризующее баллистические свойства НАСП);
- более простой способ согласования расчетных и экспериментальных значений баллистических элементов (уточняются не кривые моментных и силовых аэродинамических характеристик, а только одно число).
Кроме того, выбор упрощенного варианта решения задачи баллистики до недавнего времени определялся скромными успехами бортовой вычислительной техники.
Главным недостатком решения основной задачи внешней баллистики по сравнению с решением общей задачи является повышение требований к разработке баллистически подобных НАСП. Однако это требование может быть в значительной степени смягчено, если учесть, что в результате согласования расчетных и экспериментальных значений баллистических элементов происходит уточнение баллистической характеристики НАСП. Это уточнение в некоторой степени учитывает также и не принимаемые в основной задаче в расчет колебания НАСП вокруг центра массы. Кроме того, требование к баллистическому подобию НАСП смягчается, если брать не один, а несколько законов сопротивления.
В прецизионных системах управления требуется высокая точность решения задачи в масштабе реального времени, что накладывает высокие требования по быстродействию и емкости запоминающих устройств бортовых цифровых вычислительных систем. Современные успехи вычислительной техники позволили существенно улучшить эти характеристики, что, в свою очередь, делает более реальным более полное решение не только основной, но и общей задачи внешней баллистики.
Представим классификацию и характеристики НАСП.
В состав системы неуправляемых авиационных средств поражения входят [13]:
- авиационные бомбардировочные средства поражения (АБСП);
- неуправляемые авиационные ракеты (НАР);
- боеприпасы к авиационному автоматическому оружию: авиационным пушкам и пулеметам.
Основными характеристиками НАСП, оказывающими влияние на решение задач внешней баллистики и целевого применения, являются:
- калибры;
- диапазон допустимых условий боевого применения;
- баллистические характеристики (БХ);
- характеристики поражающего действия.
Калибром АБСП называют его номинальную массу в килограммах. Для каждого калибра установлены определенные габаритные и конструктивные характеристики: общая длина, диаметр корпуса, размах стабилизатора и т. д. В настоящее время для состоящих на вооружении АБСП установлены следующие калибры: 0,5; 1,0; 2,5; 10; 25; 50; 100; 250; 500 кг. Существуют АБСП больших калибров, однако современными БАК фронтовой авиации они не применяются.
По своим конструктивным схемам, определяющим условия боевого применения и особенности баллистических траекторий, АБСП подразделяются на две группы:
- с неизменяющимися в полете баллистическими характеристиками;
- в конструкции которых имеются тормозные устройства, обеспечивающие возможность бомбометания с малых и предельно малых высот, или, напротив, разгонные двигатели.
Калибром НАР называют максимальный диаметр ее двигателя в миллиметрах. На вооружении Военно-воздушных сил состоят НАР калибра 57, 80, 240 и 266 мм.
Неуправляемые авиационные ракеты имеют реактивный двигатель твердого топлива, который работает в течение 0,5 ÷ 2,0 с и сообщает ракете дополнительную скорость 400 ÷ 650 м/с – активный участок полета. После окончания работы двигателя ракета движется по баллистической траектории – пассивный участок полета.
Калибром снаряда называют его диаметр в миллиметрах. На вооружении Военно-воздушных сил состоят патроны со снарядами калибра 23, 30 и 37 мм.
Диапазон допустимых условий боевого применения НАСП включает данные о допустимых минимальных и максимальных значениях скорости и высоты применения для различных значений угла наклона траектории, наклонной дальности до точки интереса, а в некоторых случаях – о допустимой продолжительности полета на определенных значениях скорости и высоты.
Ограничения по максимальным значениям высоты и скорости определяются характеристиками устойчивости НАСП, прочностью их корпуса, кинетическим нагревом и конструктивными особенностями, а по минимальным – условиями безопасности носителя, исключающими возможность его поражения осколками разорвавшихся НАСП, и характером зависимости боевой эффективности от условий применения.
Поражающее действие НАСП определяется типом, калибром и конструктивными характеристиками боеприпасов, типом цели, характеристиками ее уязвимости и условиями боевого применения.
Баллистические характеристики НАСП используются при вычислении элементов их траекторий для решения задач прицеливания, оценки эффективности и безопасности боевого применения.
В качестве основной баллистической характеристики НАСП в КБО для БАК разных поколений использовались баллистический коэффициент с и характеристическое время θ. В вычислительных системах КБО для БАК поколения “4+” в качестве основной БХ НАСП применяется характеристическая скорость 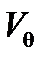 . Представим определения и формулы для расчета указанных параметров.
. Представим определения и формулы для расчета указанных параметров.
Величина баллистического коэффициента с определяется по формуле:
- для АБСП простой баллистической схемы:
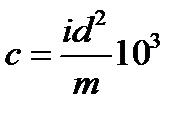 ;
;
- для НАР:
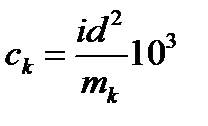 ,
,
где d – диаметр поперечного сечения НАСП;
m – масса НАСП;
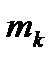 – масса НАР на пассивном участке траектории;
– масса НАР на пассивном участке траектории;
i – коэффициент формы, представляющий собой среднее отношение коэффициента лобового сопротивления 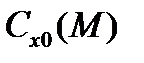 данного НАСП к эталонному коэффициенту лобового сопротивления
данного НАСП к эталонному коэффициенту лобового сопротивления 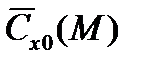 на диапазоне чисел M, проходимом объектом при данных конкретных условиях применения:
на диапазоне чисел M, проходимом объектом при данных конкретных условиях применения:
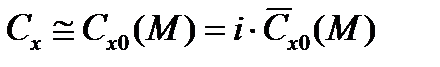 .
.
Функция 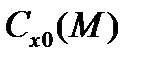 зависит, прежде всего, от геометрической формы НАСП. В КБО для БАК первых поколений, имевший ограниченные вычислительные возможности, было признано нецелесообразным иметь для каждого НАСП индивидуальную функцию
зависит, прежде всего, от геометрической формы НАСП. В КБО для БАК первых поколений, имевший ограниченные вычислительные возможности, было признано нецелесообразным иметь для каждого НАСП индивидуальную функцию 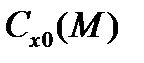 . Поэтому для НАСП некоторой формы определялась средняя (эталонная) зависимость
. Поэтому для НАСП некоторой формы определялась средняя (эталонная) зависимость 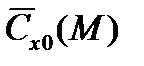 , называемая законом сопротивления. Коэффициент формы i равен средней величине отношения аэродинамического коэффициента
, называемая законом сопротивления. Коэффициент формы i равен средней величине отношения аэродинамического коэффициента 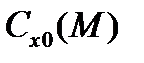 к соответствующему закону сопротивления:
к соответствующему закону сопротивления:
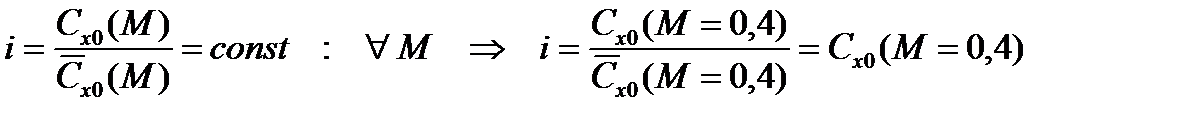 .
.
Величина баллистического коэффициента данного НАСП зависит от того, по отношению к какому закону сопротивления он определен. В связи с этим всегда, когда приводится значение баллистического коэффициента, указывается, по отношению к какому закону он определен. Одним из первых законов сопротивления, получивших широкое распространение, был закон, предложенный итальянским баллистиком Сиаччи. Наряду с законом Сиаччи в авиации используются специальные законы сопротивления для НАСП.
Характеристическое время НАСП есть, по определению, время падения НАСП с высоты 2000 м при скорости бросания, равной 40 м/с, угле бросания, равном нулю, и при нормальных атмосферных условиях. Величина характеристического времени конкретного НАСП зависит от того, какие допущения приняты в отношении формы и размеров Земли (плоская или сферическая), и от типа нормальных атмосферных условий.
Как уже отмечалось, в КБО современных БАК в качестве БХ НАСП используется характеристическая скорость 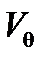 .
.
Характеристическая скорость НАСП 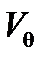 определяется как некоторая условная скорость, вычисленная из условия равенства ускорения свободного падения
определяется как некоторая условная скорость, вычисленная из условия равенства ускорения свободного падения 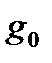 на поверхности Земли и ускорения за счет силы лобового сопротивления при нормальной плотности воздуха
на поверхности Земли и ускорения за счет силы лобового сопротивления при нормальной плотности воздуха 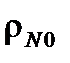 на поверхности Земли и постоянном дозвуковом значении коэффициента лобового сопротивления НАСП
на поверхности Земли и постоянном дозвуковом значении коэффициента лобового сопротивления НАСП 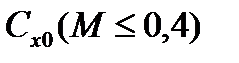 .
.
В соответствии с определением характеристическая скорость 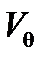 вычисляется по формуле:
вычисляется по формуле:
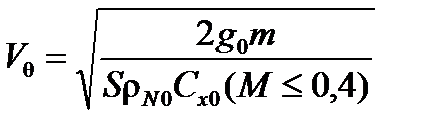 ,
,
где S – площадь поперечного сечения НАСП, м2.
Принятие в качестве характеристик НАСП соответствующего ему нормированного закона сопротивления 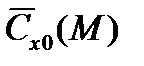 и характеристической скорости
и характеристической скорости 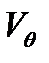 равносильно описанию баллистических качеств НАСП с помощью параметров m, S и индивидуальной зависимости Cx0 (M).
равносильно описанию баллистических качеств НАСП с помощью параметров m, S и индивидуальной зависимости Cx0 (M).
Дополнительными БХ НАР являются: полный импульс РД J, время работы РД 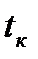 , начальная масса НАСП
, начальная масса НАСП 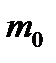 , масса порохового заряда
, масса порохового заряда 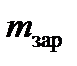 , площадь выходного сечения сопел
, площадь выходного сечения сопел 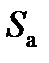 и дульная скорость НАСП.
и дульная скорость НАСП.
Кроме того, различают свободное и принудительное отделение НАСП от держателей и узлов подвески. При принудительном отделении в момент сбрасывания НАСП на него дополнительно действуют силы отталкивания различных механических, пневматических или пиротехнических силовых приводов.
Рассмотрим силы и моменты, действующие на НАСП в полете [14].
Совместное действие всех сил в процессе полета НАСП не позволяет выделить и определить экспериментально величину каждой из них. Поэтому при расчетном определении каждого из действующих факторов принимается принцип независимости действия сил (принцип суперпозиции).
Сила тяжести. На тело, вращающееся вместе с Землей, кроме силы тяготения действует центробежная сила, вызванная вращением Земли. Совместное их действие определяет силу тяжести, то есть:
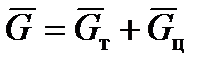 ,
,
где 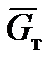 – вектор силы земного тяготения;
– вектор силы земного тяготения;
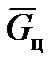 – вектор центробежной силы.
– вектор центробежной силы.
Уравнение для силы земного тяготения согласно второму закону Ньютона имеет вид:
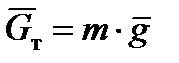 ,
,
где 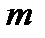 – масса НАСП:
– масса НАСП:
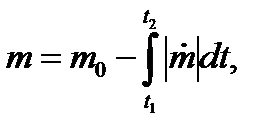
где 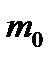 – начальная масса НАСП;
– начальная масса НАСП;
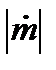 – секундный массовый расход;
– секундный массовый расход;
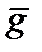 – вектор ускорения свободного падения.
– вектор ускорения свободного падения.
В сферических геоцентрических координатах центробежная сила, действующая на тело массы 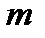 в направлении, перпендикулярном оси вращения Земли:
в направлении, перпендикулярном оси вращения Земли:
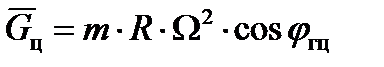 ,
,
где 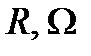 – радиус и угловая скорость вращения Земли;
– радиус и угловая скорость вращения Земли;
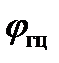 – геоцентрическая широта;
– геоцентрическая широта;
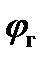 – географическая широта.
– географическая широта.
Направление свободного падения совпадает с направлением отвеса, то есть с вертикалью в данной точке земной поверхности. Отличие 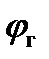 от
от 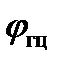 мало и составляет 11,5 угл.мин. при
мало и составляет 11,5 угл.мин. при 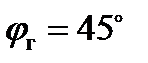 .
.
Для величин 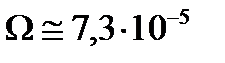 1/с,
1/с, 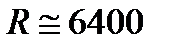 км отношение центробежного ускорения
км отношение центробежного ускорения 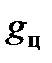 к ускорению свободного падения:
к ускорению свободного падения:
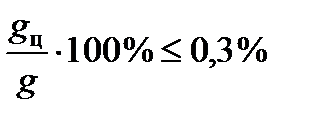 .
.
С учетом этого при выполнении баллистических расчетов погрешностью от неучета центробежного ускорения будем пренебрегать.
Сила Кориолиса:
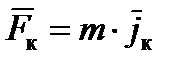 .
.
Кориолисово ускорение 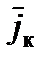 , возникающее за счет вращения Земли при наличии относительной скорости
, возникающее за счет вращения Земли при наличии относительной скорости 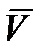 , определяется зависимостью:
, определяется зависимостью:
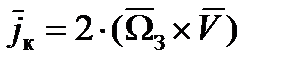 .
.
Модуль кориолисова ускорения:
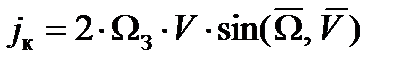 ,
,
где 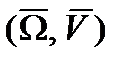 – угол между векторами
– угол между векторами  и
и 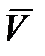 .
.
При 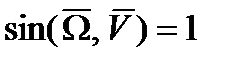 и
и 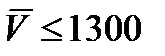 м/с:
м/с:
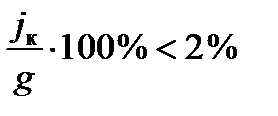 .
.
Расчеты показывают, что влияние вращения Земли на полет НАСП целесообразно учитывать, начиная с дальности примерно 30 000 м.
Сила тяги. Некоторые НАСП, например НАР, имеют реактивные двигатели, создающие силу тяги 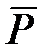 :
:
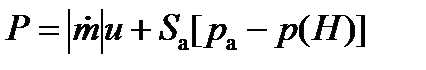 ,
,
где 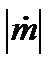 – секундный массовый расход топлива;
– секундный массовый расход топлива;
u – скорость истечения газов;
Sa – площадь среза сопла; 
pa – давление истекающих газов на срезе сопла;
p(H) – атмосферное давление.
Движущиеся в атмосфере летательные аппараты и отделяемые средства испытывают действие аэродинамических сил. Величина и направление аэродинамических сил (и их моментов) зависят от параметров атмосферы. Исследование основных характеристик атмосферы приведено в последующем изложении.
Кроме того, для полного определения аэродинамических сил необходимо ввести ряд параметров, характеризующих как пространственную ориентацию векторов сил, так и отдельные функции состояния атмосферы и условия старта НАСП.
Угол нутации 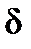 :
:
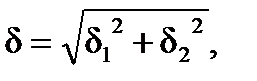
где 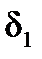 – угол атаки НАСП;
– угол атаки НАСП;
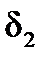 – угол скольжения НАСП.
– угол скольжения НАСП.
Число Маха M:
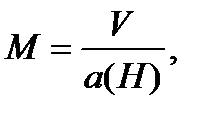
где 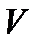 – воздушная скорость НАСП;
– воздушная скорость НАСП;
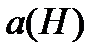 – скорость звука.
– скорость звука.
Площадь миделя НАСП S:
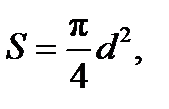
где d – диаметр НАСП.
Скоростной напор набегающего невозмущенного потока 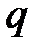 :
:
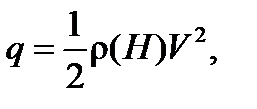
где 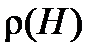 – плотность воздуха.
– плотность воздуха.
Сила лобового сопротивления атмосферы 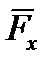 направлена противоположно вектору воздушной скорости НАСП и с учетом угла нутации
направлена противоположно вектору воздушной скорости НАСП и с учетом угла нутации 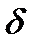 записывается в следующем виде:
записывается в следующем виде:
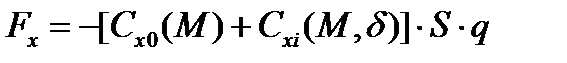 ,
,
где 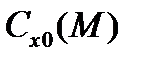 – коэффициент силы лобового сопротивления при нулевом угле нутации;
– коэффициент силы лобового сопротивления при нулевом угле нутации;
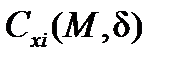 – коэффициент индуктивного сопротивления, зависящий от угла нутации
– коэффициент индуктивного сопротивления, зависящий от угла нутации 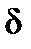 ;
;
q – скоростной напор набегающего невозмущенного потока;
S – площадь миделя НАСП.
В свою очередь, выражение для коэффициента индуктивного сопротивления 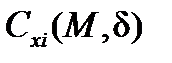 имеет следующий вид:
имеет следующий вид:
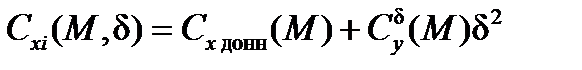
где 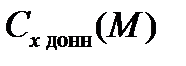 – коэффициент донного сопротивления НАСП;
– коэффициент донного сопротивления НАСП;
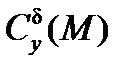 – производная коэффициента нормальной силы по углу нутации.
– производная коэффициента нормальной силы по углу нутации.
Нормальная (подъемная) сила 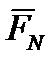 пропорциональна углу нутации
пропорциональна углу нутации 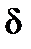 и лежит в плоскости сопротивления.
и лежит в плоскости сопротивления.
Сила Магнуса 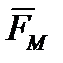 возникает вследствие вращения НАСП вокруг продольной оси при ненулевом угле нутации
возникает вследствие вращения НАСП вокруг продольной оси при ненулевом угле нутации 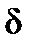 . При вращении НАСП частицы набегающего потока воздуха, встречаясь с частицами воздуха, увлеченными во вращение поверхностью НАСП, создают разность пристенного давления. Из-за перераспределения давления возникает сила, перпендикулярная плоскости сопротивления и направленная в сторону, обратную смещению встречных потоков.
. При вращении НАСП частицы набегающего потока воздуха, встречаясь с частицами воздуха, увлеченными во вращение поверхностью НАСП, создают разность пристенного давления. Из-за перераспределения давления возникает сила, перпендикулярная плоскости сопротивления и направленная в сторону, обратную смещению встречных потоков.
Система уравнений поступательного движения центра масс НАСП имеет вид:
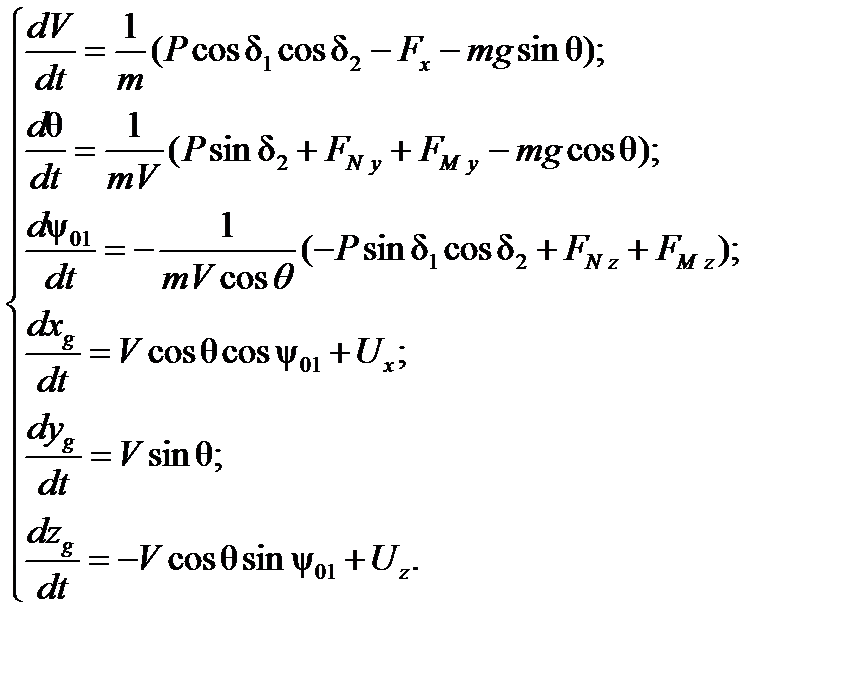
где 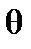 – угол наклона траектории НАСП;
– угол наклона траектории НАСП;
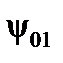 – угол разворота плоскости бросания НАСП;
– угол разворота плоскости бросания НАСП;
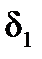 ,
, 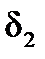 – углы атаки и скольжения НАСП.
– углы атаки и скольжения НАСП.
Векторное уравнение движения относительно центра масс целесообразно проектировать на оси связанной с НАСП системы координат. С учетом этого все составляющие момента внешних сил рассматриваются в этой системе координат. Суммарный момент внешних сил включает в себя следующие составляющие:
- статический (нормальный) момент;
- момент силы Магнуса;
- демпфирующий момент;
- момент сопротивления вращению (трения).
Рассмотрим каждый из перечисленных моментов подробно.
Статический (нормальный) момент 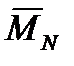 возникает вследствие того, что подъемная сила НАСП расположена не в центре масс. Название момента зависит от направления его действия в плоскости угла атаки или скольжения. Если момент увеличивает эти углы, он называется опрокидывающим, если уменьшает – стабилизирующим. Некоторые НАСП в аэродинамическом отношении являются неустойчивыми. Возникающая неустойчивость компенсируется гироскопическими свойствами НАСП.
возникает вследствие того, что подъемная сила НАСП расположена не в центре масс. Название момента зависит от направления его действия в плоскости угла атаки или скольжения. Если момент увеличивает эти углы, он называется опрокидывающим, если уменьшает – стабилизирующим. Некоторые НАСП в аэродинамическом отношении являются неустойчивыми. Возникающая неустойчивость компенсируется гироскопическими свойствами НАСП.
Момент силы Магнуса 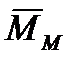 лежит в плоскости сопротивления и перпендикулярен продольной оси НАСП.
лежит в плоскости сопротивления и перпендикулярен продольной оси НАСП.
Демпфирующий момент 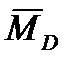 действует против направления вращения при колебаниях относительно центра масс. Он стремится затормозить (погасить) колебания НАСП и его вращение. У осесимметричных НАСП коэффициент демпфирования корпуса будет одинаков по экваториальным осям, а разница в демпфирующих моментах будет определяться различием значений угловых скоростей относительно осей Oy и Oz.
действует против направления вращения при колебаниях относительно центра масс. Он стремится затормозить (погасить) колебания НАСП и его вращение. У осесимметричных НАСП коэффициент демпфирования корпуса будет одинаков по экваториальным осям, а разница в демпфирующих моментах будет определяться различием значений угловых скоростей относительно осей Oy и Oz.
Момент сопротивления вращению (трения) 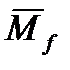 направлен вдоль продольной оси Ox в противоположном направлении по отношению к вектору угловой скорости собственного вращения.
направлен вдоль продольной оси Ox в противоположном направлении по отношению к вектору угловой скорости собственного вращения.
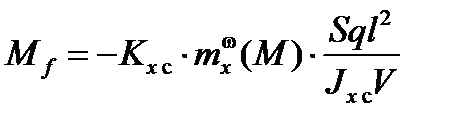 ,
,
где 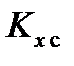 – проекция кинетического момента
– проекция кинетического момента 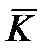 НАСП относительно центра масс на ось
НАСП относительно центра масс на ось 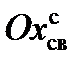 связанной с НАСП системы координат;
связанной с НАСП системы координат;
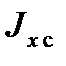 – полярный момент инерции НАСП;
– полярный момент инерции НАСП;
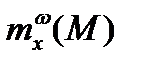 – производная коэффициента момента сопротивления вращению по безразмерной угловой скорости собственного вращения
– производная коэффициента момента сопротивления вращению по безразмерной угловой скорости собственного вращения 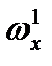 .
.
Система уравнений вращательного движения НАСП относительно центра масс в связанной с НАСП системе координат имеет вид:
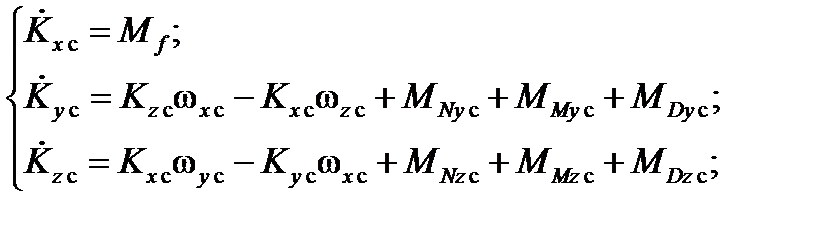
где 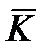 – кинетический момент НАСП относительно центра масс;
– кинетический момент НАСП относительно центра масс;
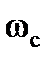 – угловая скорость вращения связанной с НАСП системы координат относительно инерциальной системы координат.
– угловая скорость вращения связанной с НАСП системы координат относительно инерциальной системы координат.
Связь между угловой скоростью 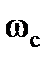 и производными углов атаки и скольжения
и производными углов атаки и скольжения 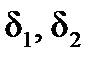 определяется следующей системой уравнений:
определяется следующей системой уравнений:
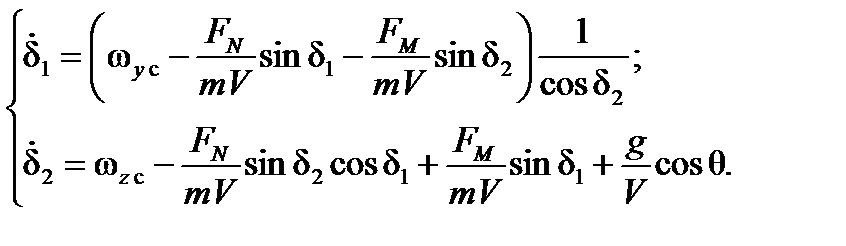
Представим упрощенную математическую модель движения НАСП в задаче прицеливания по наземным целям.
Интегрирование полной системы дифференциальных уравнений, описывающих пространственное движение НАСП, составляет общую задачу внешней баллистики. При решении задачи применения НАСП по НЦ достаточно определять движения центра масс без учета движения относительно центра масс при условии устойчивости НАСП на траектории.
С учетом изложенного выше векторное уравнение движения центра масс НАСП примет вид:
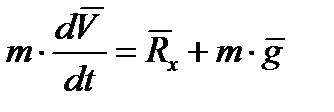 ,
,
или, в ускорениях:
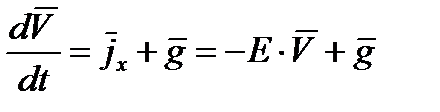 . (13)
. (13)
Ускорение силы лобового сопротивления jx равно:
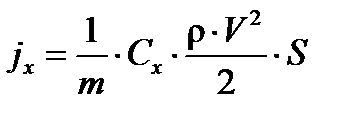 .
.
Используя введенное ранее понятие характеристической скорости Vθ , и проектируя векторное равенство на оси стартовой системы координат, окончательно будем иметь:
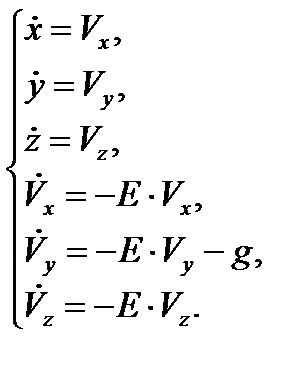 (14)
(14)
В уравнениях (13) и (14) Е – обобщенная функция сопротивления, которая рассчитывается по формуле:
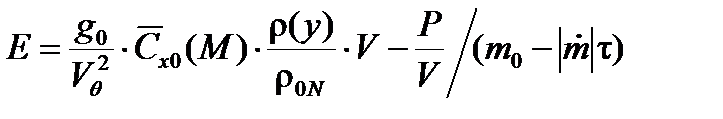 ,
,
где t – текущее время ступени НАСП, начиная с момента ее включения;
r0N и g0 – плотность воздуха и ускорение свободного падения у поверхности Земли, определенные в модели нормальной атмосферы.
Получили систему шести нелинейных уравнений первого порядка с шестью неизвестными. Начальными условиями в точке сбрасывания или пуска НАСП в момент времени 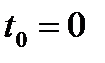 для системы (14) являются:
для системы (14) являются:
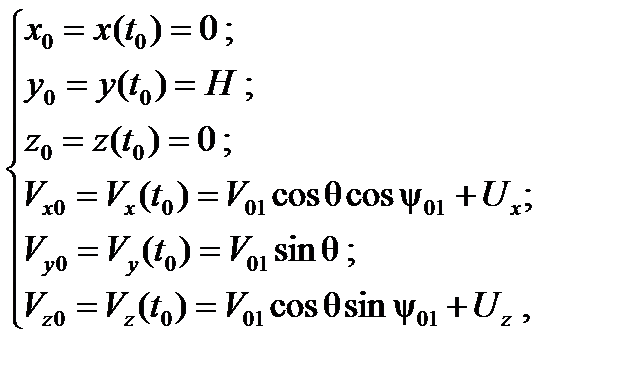
где H – высота точки старта НАСП.
Баллистические элементы НАСП в точке падения определяются при условии 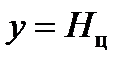 . Из второго уравнения (14) можно найти значение времени падения T, полагая в нем y = 0, а относ A определяется из первого и третьего уравнений системы (14) при подстановке t = T.
. Из второго уравнения (14) можно найти значение времени падения T, полагая в нем y = 0, а относ A определяется из первого и третьего уравнений системы (14) при подстановке t = T.
Задачи определения элементов траектории НАСП можно решать двумя методами: методом “готовых решений” и непосредственным интегрированием дифференциальных уравнений движения НАСП.
Идея первого метода заключается в том, что дифференциальные уравнения движения НАСП решаются заранее в наземных условиях для некоторых обобщенных НАСП с различными БХ при всевозможных условиях применения [22]. Результаты решения сводятся в баллистические таблицы. При выполнении практических расчетов для конкретных НАСП и условий применения 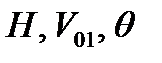 из таблиц выбираются значения баллистических элементов траектории для близких условий применения. Затем баллистические элементы траектории реальных НАСП определяются в БЦВС АПрС путем аппроксимации полученных значений под конкретные параметры применения.
из таблиц выбираются значения баллистических элементов траектории для близких условий применения. Затем баллистические элементы траектории реальных НАСП определяются в БЦВС АПрС путем аппроксимации полученных значений под конкретные параметры применения.
Использование такого подхода объясняется, главным образом, ограниченными возможностями еще в недавнем прошлом бортовых вычислителей. Он обладает следующими существенными недостатками:
- ограниченный диапазон условий применения НАСП;
- трудность реализации сложных баллистических схем НАСП;
- жесткая привязанность к системе допущений, для которых составлены баллистические таблицы;
- необходимость компенсации возникающих ошибок.
В настоящее время возросшие возможности БЦВМ позволяют решать баллистические задачи методами численного интегрирования уравнений движения НАСП в конкретных условиях применения непосредственно на борту БАК в процессе прицеливания в ускоренном масштабе времени.
