Моменты инерции твердого тела

На ледовой площадке спортсмен-фигурист, чтобы достичь высокой угловой скорости соединяет ноги, выпрямляет туловище и вытягивает вверх руки, с целью же гашения скорости (в конце выступления) руки разбрасывает по сторонам. Из приведенного примера видно, что на кинематику механической системы оказывают влияние не только массы, но и взаимное их расположение.

Известно, что при поступательном движении, мерой инерции твердого тела является масса. Тогда как при вращательном движении инертность тела определяется распределением его массы относительно оси вращения, т.е. моментом инерции.

Так, например, при прочих равных условиях (рис.3.19) поступательного движения, тело 1 имеющее большую массу, до остановки, будет двигаться дольше легкого тела 2. При равных массах тела остановятся одновременно. В случае же вращения тел одинаковой массы (рис.3.19), тело 2, точки которого расположены дальше от оси вращения, чем у тела 1, до остановки будет вращаться дольше, чем тело 1, масса которого сконцентрирована возле оси.

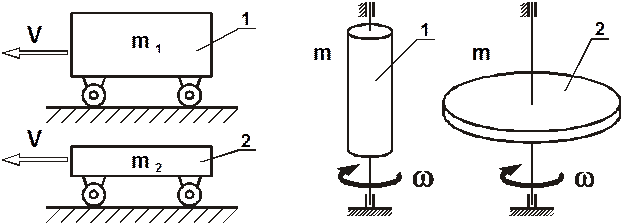
Рис.3.19.

Момент инерции относительно точки (полюса)- скалярная величина, численно равная сумме произведений масс всех материальных точек тела (системы) на квадрат расстояния до полюса:

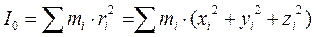
Момент инерции относительно оси- скалярная величина, численно равная сумме произведений масс всех материальных точек тела (системы) на квадрат расстояния до оси:

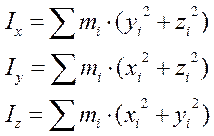
Момент инерции тела относительно плоскости- скалярная величина, численно равная сумме произведений масс всех материальных точек тела (системы) на квадрат расстояния до плоскости:

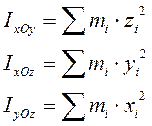
Центробежный момент инерциитела относительно какой- либо пары координатных осей - скалярная величина, равная сумме произведений массы каждой точки тела на произведение её координат по этим осям.

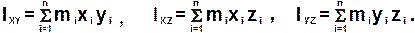
Центробежные моменты инерции, в отличии от осевых, могут быть отрицательными и равными нулю.

Зависимости между моментами инерции твердого тела относительно координатных осей, координатных плоскостей и начала координат имеют вид:

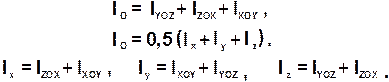
Момент инерции относительно оси произвольного направления.

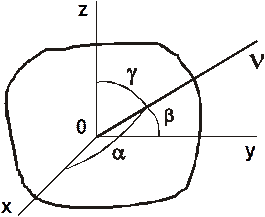
Рис. 3.20.

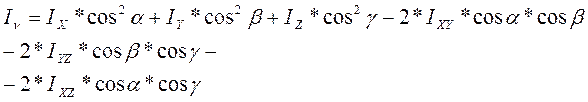
где 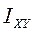, , 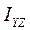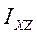-центробежные моменты инерции.

Радиус инерции

Момент инерции твердого тела относительно заданной оси, например оси z, можно представить в виде:

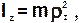
где ρ - радиус инерции тела относительно оси z.

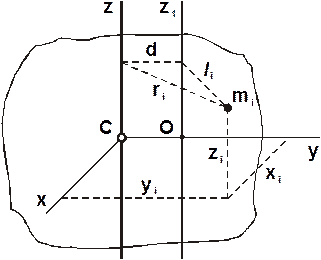
Радиус инерции определяет то расстояние от оси, (рис. 3.21) на котором нужно сосредоточить всю массу тела, чтобы она имела тот же момент инерции, как и рассматриваемое тело.

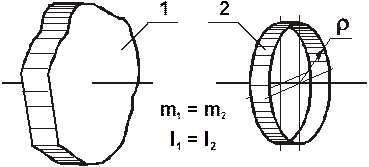
Рис. 3.21.

Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса Штейнера)

Моменты инерции данного тела относительно разных осей будут иметь различное значение. Зависимость между моментами инерции тела относительно двух параллельных осей, одна из которых проходит через центр масс тела, определяется по теореме Гюйгенса.

Согласно ей: момент инерции относительно произвольной оси равен моменту инерции относительно оси, проходящей через центр масс параллельно данной оси плюс произведение массы тела на квадрат расстояния между ними.

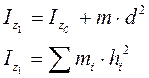, где h- расстояние от каждой точки до оси z₁.

Докажем данную теорему

Исходя из определения момента инерции относительно оси, запишем

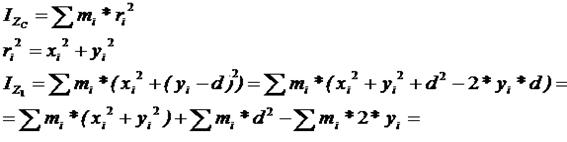
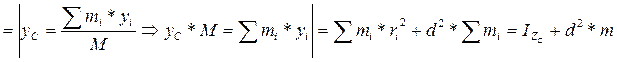
Из формулы Гюйгенса видно, что при удалении оси Z₁ от оси Z в3уличина момента инерции возрастает. Следовательно, из всех осей данного направления наименьший момент инерции будет относительно оси проходящий через центр масс.