Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пе­ресекающиеся поверхности должны иметь семейство круговых сече­ний.

13.4.1 Задание:даны две поверхности вращения - тор и конус, оси которых находятся в одной плоскости, параллельной П₁ (рис. 13.7). Требуется построить линии их пересечения.

Решение:прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след 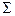₂ фронтально проецирующей плоскости 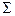. Линия пересечения её с поверхностью тора - окруж­ность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомо­гательной секущей сферой по окружности, её центр должен находить­ся на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса (O₂) выбирается центром вспомогатель­ной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости 1.2- Такая вспомога­тельная секущая сфера пересекает кольцо и конус вращения по ок­ружностям, фронтальные проекции которых - отрезки прямых. Точка пресечения этих отрезков 3₂ (рис. 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции - точки 4₂ - О'₂. Горизон­тальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, кону­са.

ЛИТЕРАТУРА

1. Гордон В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. — М.: Высшая школа, 2000. — 272 с.

2. Гордон В.О. Сборник задач по курсу «Начертательная геомет­рия» / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева. - М.: Высшая школа,2000.

3. Чекмарев А.А. Инженерная графика. - М.: Высшая школа, 1998.-365с.

4. Фролов С.А. Начертательная геометрия. - М.: Высшая школа,1983.-240 с.

5. Арустамов Х.А. Сборник задач по начертательной геометрии. -М.: Машиностроение, 1978. -445 с.

ОГЛАВЛЕНИЕ

	ВВЕДЕНИЕ
1.	ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
2.	ОБРАЗОВАНИЕ ПРОЕКЦИЙ. МЕТОДЫ ПРОЕЦИРОВАНИЯ
3.	ПРОЕЦИРОВАНИЕ ТОЧКИ
4.	ПРЯМАЯ. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
5.	ПЛОСКОСТЬ
6.	ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ
7.	ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ ИПЛОСКОСТИ
8.	ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ К ПЛОСКОСТИ
9.	СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
10.	МНОГОГРАННИКИ. СЕЧЕНИЕ МНОГОГРАННИКОВ ПЛОСКОСТЬЮ. РАЗВЕРТКИ МНОГОГРАННИКОВ
11.	ПОВЕРХНОСТИ ВРАЩЕНИЯ.ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ ПЛОСКОСТЬЮ. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
12.	ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
13.	ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
	ЛИТЕРАТУРА

Учебное электронное и текстовое издание