Идеальный газ и его законы

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной? энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Уравнение состояния идеального газа имеет вид:
pVm = RT; Законы: 1. Изохорический процесс. Закон Шарля. V = const. 2. Изобарический процесс. Закон Гей-Люссака. Р = const.
3. Изотермический процесс. Закон Бойля – Мариотта. T = const. 4. Адиабатический процесс Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. 6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится N_A=6,02·10²³молекул (число Авогадро)7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов: 8. Объединённый газовый закон (Закон Клапейрона).

Предмет и методы молекулярной физики.

Основная задача молекулярной физики заключается в том, чтобы объяснить физические свойства вещества, существующего в различных агрегатных состояниях, с позиций его молекулярно-кинетического строения.Фундамент молекулярно-кинетической теоории(мкт) составляют 3 положения: 1)все вещества состоят из из мельчайших частиц (атом и молекул).2) между атомами и молекулами вещества действуют силы притяжения и отталкивания 3) атомы и молекулы вещества непрерывно и хаотично движутся. Молекулярная физика изучает : 1. молек. строение газов, жидк. и твердых тел; 2. явления в этих средах, обусл. молек. движением; 3. процессы в веществе при внешних воздействиях; 4. процессы перехода вещества из одного агрегатного состояния в другое 5. явления на границах между веществами в разных состояниях .

55. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: (при Vm = 22,4, p=1x10^5 Па) Так как , где — количество вещества, а , где — масса, — молярная масса, то

Работа при изопроцессах.

изобарный процесс - термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа. Работа А=PdV (где P – давление газа, а dV изменение объёма), на графике P-V площадь фигуры.изохорный процесс- термодинамический процесс, который происходит при постоянном объёме (работа = 0, т.к. объём неизменен). Проверка: по определению , проинтегрировав видно что А=0.изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. Работа, совершенная идеальным газом в изотермическом процессе, равна , где — число частиц газа, — температура, и — объём газа в начале и конце процесса, — постоянная Больцмана. Q=A.

57. адиаба́тный проце́сс — термодинамический процесс, при котором система не обменивается тепловой энергией с окружающим пространством Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит^[8]: Работа равна где — давление газа, малое приращение объёма. Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением^[6][15][16] (Адиабата Пуассона) где — его объём, — показатель адиабаты, и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

58. Первый закон термодинамики. Теплоемкость газов.— один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем. Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Первое начало термодинамики:1)при изобарном процессе 2)при изохорном процессе ( ) 3)при изотермическом процессе .Здесь — масса газа, — молярная масса газа, — молярная теплоёмкость при постоянном объёме, — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT: СИ — Дж/К. Теплоёмкость газа сильно зависит от характера процесса, который с ним протекает. Наиболее часто используются изохорная теплоёмкость и изобарная ; для идеального газа . .

59. Процесс Джоуля-Томсона.Эффе́ктом Джо́уля-То́мсона называется изменение температуры газа при адиабатическом медленном протекании газа под действием постоянного перепада давлений сквозь пористую перегородку. Данный эффект является одним из методов получения низких температур. Изменение энергии газа в ходе этого процесса будет равно работе: . Изменение температуры при малом изменении давления (дифференциальный эффект) в результате процесса Джоуля — Томсона определяется производной , называемой коэффициентом Джоуля — Томсона. Выражение для этого коэффициента: где — теплоёмкость при постоянном давлении. Для идеального газа , а для реального газа он определяется уравнением состояния. , то эффект называют отрицательным, и наоборот , то положительным. Температуру, при которой меняет знак, называют температурой инверсии.

60 Необратимость тепловых процессов. Второй закон термодинамики.Первый закон термодинамики не устанавливает направления тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми . Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. является постулатом, не доказываемым в рамках термодинамики. Иная формулировка: Энтропия изолированной системы не может уменьшаться.Энтропия – мера необратимости рассеивания энергии, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно

62. Энтропия. Закон возрастания энтропии.

Энтропия – мера необратимости рассеивания энергии, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно . Формулировка закона: «В изолированной системе энтропия не уменьшается», т.е. если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает — увеличивается или в предельном случае остается постоянной. Вероятность перехода в состояния с большей энтропией настолько подавляюще велика по сравнению с вероятностью сколько-нибудь заметного ее уменьшения, что последнее вообще фактически никогда не может наблюдаться в природе.

61. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется. Цикл Карно состоит из четырёх стадий: 1 Изотермическое расширение (объём рабочего тела увеличивается) 2 Адиабатическое расширение (температура уменьшается до температуры холодильника) 3 Изотермическое сжатие (отдаётся теплота холодильнику) 4 Адиабатическое сжатие (температура увеличивается до температуры нагревателя)

63. Фазовые переходы. Формула Клайперона-Клаузиуса. Критическая точка.Фа́зовый перехо́д -переход вещества из одной термодинамической фазы в другую при изменении внешних условий. Наиболее распространённые примеры фазовых переходов первого рода: плавление и кристаллизация, испарение и конденсация, сублимация и десублимация. При фазовом переходе второго рода плотность и внутренняя энергия не меняются. Наиболее распространённые примеры фазовых переходов второго рода: прохождение системы через критическую точку, переход металлов и сплавов в состояние сверхпроводимости, переход аморфных материалов в стеклообразное состояние. Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление и др.). Согласно уравнению, теплота фазового перехода (например, теплота плавления) при квазистатическом процессе определяется выражением где — удельная теплота фазового перехода, — изменение удельного объёма тела при фазовом переходе. Критическая точка — сочетание значений температуры и давления , при которых исчезает различие в свойствах жидкой и газообразной фаз вещества. Для смеси веществ критическая температура не является постоянной величиной и может быть представлена пространственной кривой, крайними точками которой являются критические температуры веществ

64/Реальные газы. Уравнение Ван-дер-Вальса.. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. уравнения состояния реального газа описывается уравнениемВан-дер-Ваальса. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия становится функцией не только температуры, но и объёма. Для одного моля газа Ван-дер-Ваальса оно имеет вид: учитывает силы притяжения между молекулами — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами). Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так: Внутренняя энергия Ван-дер-Ваальса для одного моль газа: .Где — молярная теплоёмкость при постоянном объёме, которая предполагается не зависящей от температуры.

24.ПОСТУЛАТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА.Эйнштейн сформулировал два положения, которые впоследствии стали называться постулатами специальной теории относительности:

· Скорость распространения света в вакууме одинакова во всех инерциальных системах отсчета и имеет наибольшее значение в сравнении со скоростями всех явлений и процессов, существующих в природе;

· Все физические явления, в том числе электромагнитные, протекают совершенно одинаково во всех инерциальных системах отсчета.

Преобразования Лоренца, связывающие координаты и время в инерциальных системах К и К’ должны удовлетворять следующим требованиям:

· Формулы преобразования должны быть симметричными относительно обеих систем отсчета;

· Если некоторая точка имеет конечные значения координат в одной системе отсчета, то в другой системе отсчета координаты этой точки также должны иметь конечные значения;

· Если скорость движения системы К' относительно К стремится к нулю, формулы преобразования должны приводить к тождествам

· Из формул преобразования следует закон сложения скоростей, в рамках которого скорость света в вакууме получается одинаковой во всех инерциальных системах отсчета.

46. Два способа определения вероятности. Вероятность обнаружить молек. В данной точке сосуда.
P1=V/2/V=0.5
P2=V/4/V=0.25
dPn=dV/v
dW=P(V)dV/V
Или в зависимости от времени нахождения частицы в данной точке сосуда за все время наблюдений
dW=dt/t
dW=P(T)dt/t

26.СЛОЖЕНИЕ СКОРОСТЕЙ (РЕЛЯТИВИСТСКОЕ).Закон сложения скоростей справедлив при скорости движения тел и систем отсчета, значительно меньшей скорости света в вакууме. Найдем релятивистский закон преобразования скорости частицы при переходе от системы отсчета К и системе К’ движущейся относительно К. Воспользуемся преобразованием Лоренца:

Легко/видеть:

Поскольку имеем Используя релятивистский закон получим: . Если V<<C, то выражение принимает нерелятивистский вид .

29.Релятивистская динамика. Связь p и E.Все уравнения, описывающие все законы природы, должны быть инвариантными относительно преобразования Лоренца.

ЗСЭ и ЗСИ не выполняются. E=jmc^2; p=jmV

J=1/(1-V^2/c^2)^1/2

m=m0/(1-V^2/c^2)^1/2- релятивистская масса. Масса не зависит от движения системы отсчета.

(E/(mc^2))^2-(p/(mc^2))^2=1/(1-V^2/c^2)- V^2/c^2/(1-V^2/c^2)=1

E=pc^2/V

41.РЕЗОНАНС ПРИ ВЫНУЖДЕННЫХ КОЛЕБАНИЯХ. БИЕНИЯ.В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ0, происходит резкое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ0 внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой.Биения – это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами. Пусть частота одного колебания ω1=ω, а частота второго колебания ω2=ω+Δω, причем, Δω<<ω. Амплитуды обоих колебаний равна A.x1=A·cosωt x2=A·cos(ω+Δω)t Складываем эти выражения.Aбиений=|2Acos(Δω/2)t|x=|2Acos(Δω/2)t|cosωt – уравнение биений.

30. ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА.Движение твёрдого тела можно представить как результат суммы поступательного (любая связанная с телом прямая перемещается параллельно самой себе, т.е. все точки тела движутся по одинаковым траекториям) и вращательного (все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемою осью вращения; все окружности лежат в параллельных плоскостях и перпендикулярно оси вращения) движений (неоднозначно). Произвольная точка твёрдого тела испытывает перемещение 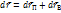, причём 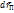для всех точек тела одно и то же. Разделив 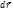на соответствующий промежуток времени 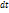, получим скорость точки: 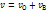. 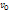– одинаковая для всех точек скорость поступательного движения, 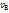– скорость, обуславливаемая вращением (различная в разных точках).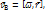 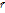– радиус-вектор данной точки, 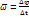– угловая, независящая от выбора точки О скорость. Следовательно, 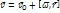. Любое твёрдое тело можно представить как совокупность материальных точек массы 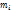, расстояние между которыми неизменно. Каждая материальна точка движется под действием, как внутренних сил, так и внешних. Движение определяется 2-ым законом Ньютона. 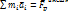. 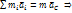.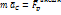Центр масс твёрдого тела движется таким же образом, как двигалась бы материальная точка массы 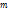под действием всех внешних сил.Движение твёрдого тела определяется 2-мя (3-мя) уравнениями:

1)

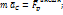
2) ;

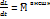3) 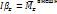– при плоском движении

38.ПРИВЕДЕННАЯ ДЛИННА ФИЗИЧЕСКОГО МАЯТНИКА.Приведенная длина физического маятника: Приведенная длина физического маятника всегда больше l. Действительно, согласно теореме Штейнера где - момент инерции маятника относительно оси.Разделив на ml:

и

35.УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ И ЕГО РЕШЕНИЕ.Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса: Или где A - амплитуда;

ω - круговая частота; α - начальная фаза; ( ωt + α ) - фаза.

Уравнение гармонических колебаний: Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество, которая имеет вид

22/Связь законов сохранения и однородностью и изотропией пространства. Изотропия – инвариантность физических законов, свойственных рассматриваемой системе, относительно определенных преобразований величин, используемых в формулировке этих законов.
Законы сохранения энергии, импульса и момента импульса связаны со свойствами симметрии пространства и времени (изотропия).
Наиболее важными являются следующие преобразования
симметрии пространства и времени:
- преобразование переноса, которое сводится к переносу системы из одной области пространства в другую параллельно самой себе, т.е. без изменения ее ориентации;
- преобразование поворота системы в пространстве;
- преобразование времени, при котором одно и то же явление начинается в различные моменты.
Если замкнутую систему перенести из одной области пространства в другую без изменения условий, в которых находились тела системы, такой перенос не отражается на протекании в ней физических явлений (однородность).

35/Уравнение гармонических колебаний и его решение. Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат Х около положения равновесия, принятого за начало координат. Тогда зависимая от времени координата Х задается уравнением аналогичным уравнению, где S=Х; ; закон Гука: => ; ; . Решением этого уравнения является :

где A, ω, и φ — это постоянные величины, и положение равновесия принимается за начальное.[1] Каждая из этих постоянных представляет собой важное физическое

свойство движения: A — это амплитуда, ω = 2πf —

это круговая частота, и φ — начальная фаза.

Барометрическая формула.

Давление на высоте h+dh будет p+dp, причем если dh >0, то dp < 0, так как вес вышележащих слоев атмосферы, а следовательно и давление с высотой убывают.Разность давления: p-(p+dp)= ρgdh, где ρ-плотность газа на высоте h,=> dp=- ρgdh. dp=-(Mg)/(RT)dh. T=const => lnp=-(Mgh)/(RT)+lnC, p=C exp(-(Mgh)/(RT)),подставим h=0,получим что C=p_o,=> p=p₀ exp(-(Mgh)/(RT)) эта формула наз. Бараметрической. Из нее следует, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже температура.

Опыт Майкельсона и Морли.

В классической механике v<<c . С . В СТО рассматриваются случаи, когда v~c. Тогда считалось, что в пространстве эфир.

Опыты Майкельсона и Морли являются независимыми от или источника.

Опыт: Пусть на жёстком основании длиной D имеется источник света и отражающее зеркало. -> вправо обратно. Теперь повернём установку на угол .

; ; ;

Подставляем. Получаем: ;

; Считаем t’. Считаем t-t’=…= .

Замедление времени.t – время, за которое луч достиг до зеркала.А и В – 2 часов. На В есть кисточка. Когда В проходит через А, оставляет метку. Если метка на краю, то нет изменений. Если ниже, то В уменьшились. Наблюдатель, движущийся с А, увидит, что движущиеся световые часы стали короче. А с точки зрения наблюдателя за В движущиеся относительно него часы окажутся длиннее. Но по принципу ТО наблюдатели равноправны. Далее рассмотрим систему с точки зрения наблюдателя, покоящегося в системе А. Для него пусть свет луча будет представляться более длинным, чем в часах А.

; ;Этот наблюдатель видит: часы тикают реже t.Пусть есть механические и световые часы. Помещаем механические часы в движущуюся систему. Видим: световые отстали, механические не меняются.

51.Наиболее вероятная скорость молекул.Наиболее вероятная скорость молекул — это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул Данная формула вытекает из распределения Максвелла. Наиболее вероятная скорость, как показал он, зависит от температуры газа и массы молекул.Что бы получить из первой формулы скорости молекулы вторую, надо сделать всего две замены, расписать универсальную газовую постоянную, как R=N_ak, и молярную массу.M=N_am , то у нас получится из этой формулы: V— Наиболее вероятная скорость молекул.K=1,38*10^-23 — Постоянная Больцмана.T — Температура.m — Масса одной молекулы.R=8,31— Универсальная газовая постоянная M— Молярная масса. v— Количество вещества.N_a=6,02*10²³ — Число Авогадро