Цепи Маркова с дискретным временем

Пусть случайный процесс 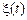изменения во времени состояний некоторой системы принимает целочисленные значения 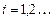из множества 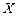конечного или счетного, то есть 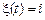, 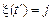. Переходы из одного состояния в другое происходят через равные промежутки времени 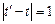, которые будем называть шагом.

Условные вероятности 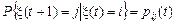, для всех 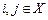образуют матрицу вероятностей переходов цепи Маркова из одного состояния в другое в момент времени .

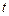Если вероятности переходов не зависят от момента времени 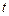, то есть 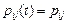, то цепь Маркова называется однородной с матрицей вероятностей переходов за один шаг

,

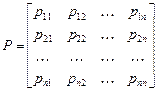
где 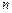– число состояний системы (число возможных значений цепи Маркова) – конечное или счетное. Элементы матрицы 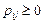и удовлетворяют условию нормировки

, .

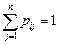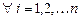Такую матрицу называют стохастической или марковской.

Для описания цепи Маркова удобно использовать граф вероятностей переходов, вершины которого обозначают возможные состояния системы, стрелки от одной вершины к другой указывают возможные переходы между состояниями, а число над стрелкой задаёт вероятность такого перехода. Например, пусть множество состояний 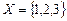, матрица вероятностей переходов имеет вид

,

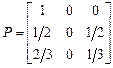тогда граф вероятностей переходов выглядит следующим образом:

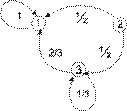
Цепь Маркова с дискретным временем полностью определяется матрицей вероятностей переходов за один шаг и начальным распределением 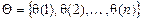, где .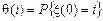

Для распределения вероятностей состояний однородной цепи Маркова имеет место следующее равенство векторов:

.

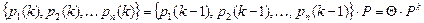Для неоднородной цепи Маркова распределение вероятностей находится по формулам

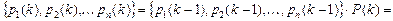
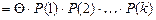
Пример.Рассмотрим состояния банка, характеризующиеся одной из процентных ставок: 12%,13%,14%, которые устанавливаются в начале каждого квартала и фиксированы на всем его протяжении.Таким образом, если за систему 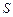принять действующую процентную ставку, то она в каждый момент времени может находиться только в одном из состояний: 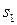– процентная ставка 12%, 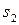– процентная ставка 13%, 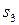– процентная ставка 14%. Анализ работы банка в предшествующие годы показал, что изменение переходных вероятностей с течением времени пренебрежимо мало. Определить распределение вероятностей состояний системы в конце года, если в конце предыдущего года процентная ставка составила 13%, а граф вероятностей переходов имеет вид:

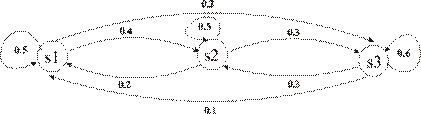
Так как множество состояний, в которых может находиться система 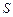, конечно, то протекающий в ней случайный процесс – дискретный. С определенной степенью погрешности можно предположить, что вероятность пребывания банка в одном из своих состояний в будущем зависит только от состояния в настоящем и не зависит от его состояний в прошлом. Поэтому рассматриваемый процесс можно считать марковским.

В силу условий банк может переходить из состояний в состояние только в определенные моменты времени 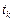– начало 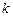-го квартала, 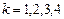, а изменение переходных вероятностей с течением времени пренебрежимо мало, то рассматриваемый процесс является однородным марковским процессом с дискретным временем.

По графу составим матрицу переходных вероятностей:

.

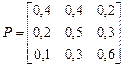Так как в конце предшествующего года процентная ставка составляла 13%, то вектор начального распределения имеет вид .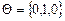

Тогда распределение вероятностей состояний процентной ставки банка в конце года, то есть по прошествии четырех кварталов определяется следующим образом:

.

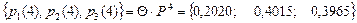Если предположить, что переходные вероятности зависят от моментов установления процентных ставок, полученный процесс будет являться неоднородной марковской цепью с дискретным временем. Например, пусть

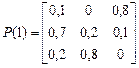
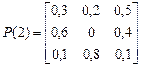
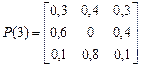
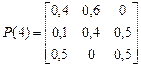
Тогда 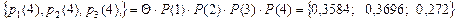.