Задачи по курсу «Электродинамика сплошных сред» и их решения
1. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.
Решение. 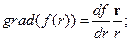
2. Вычислить 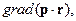
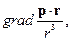
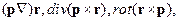 где p – постоянный вектор.
где p – постоянный вектор.
Решение. 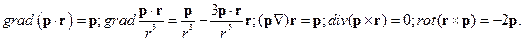
3. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:
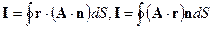
если объем, который охватывает замкнутая поверхность, равен V; A –постоянный вектор.
Решение. Умножим искомый интеграл на постоянный вектор р:
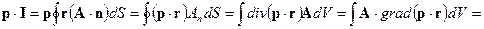
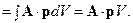
Так как вектор рпроизволен, то
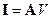 .
.
Аналогично показывается, что
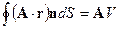
4. В равномерно заряженном шаре с объемной плотностью заряда 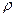 имеется шарообразная полость, центр которой расположен на расстоянии а от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и
имеется шарообразная полость, центр которой расположен на расстоянии а от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и 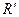 .
.
Решение. Из принципа суперпозиции полей следует, что искомая напряженность поля равна разности напряженности электрического поля, создаваемого шаром без полости, и напряженности поля зарядов, заполняющих при этом полость.
Поле внутри полости
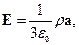
поле внутри шара (но вне полости)
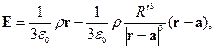
поле снаружи шара
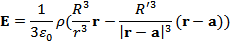
где 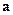 - радиус-вектор, проведенный из центра шара к центру полости.
- радиус-вектор, проведенный из центра шара к центру полости.
5. Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара. Объёмная плотность заряда равна 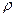 , радиус шара R.
, радиус шара R.
Решение.
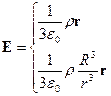
при 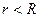
при 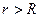
6. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.
Решение. Потенциал точечного заряда является решением уравнения
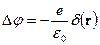 . (1)
. (1)
Представим 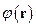 и
и 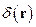 в виде разложений в интеграл Фурье:
в виде разложений в интеграл Фурье:
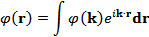
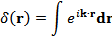
Подставляя эти разложения в уравнение (1) и приравнивая в подынтегральных выражениях коэффициенты при 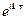 , получим
, получим
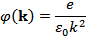
7. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону: 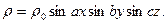
Решение. 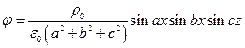 .
.
8. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.
Решение. Предположив, что заряд расположен в начале координат, решим уравнения
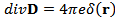
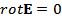
Направим оси декартовой системы координат по главным осям тензора диэлектрической проницаемости. Тогда
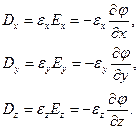
Подставим соотношения (2) в уравнение (1):
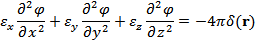
Заменой 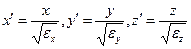 уравнение приводится к виду
уравнение приводится к виду
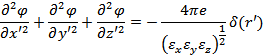
Здесь использовано свойство δ-функции:
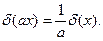
Решение уравнения (4) имеет вид
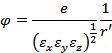
где
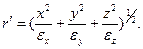
Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностьюj.Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.
Решение. H=1/2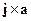
11.Найти интенсивность излучения частицы массы m, движущейся по круговой орбите радиуса a, под действием кулоновских сил. Выразить ответ через энергию частицы.
Решение. Из формулы, по которой вычисляется интенсивность дипольного излучения, где d=er, исключаемr, пользуясь уравнением движения
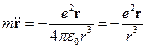
Отсюда
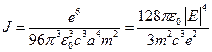
Где Е – энергия частицы.
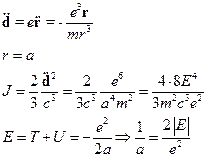
12. Определить напряженность и потенциал электростатического поля равномерно заряженного шара радиуса R. Суммарный заряд шара Q.
Ответ: 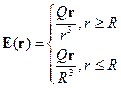
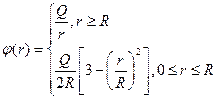
13. Вычислить энергию электростатического поля равномерно заряженного шара радиуса R. Суммарный заряд шара Q.
Ответ: 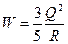 .
.
14. Средняя плотность заряда электронного облака в атоме водорода описывается функцией 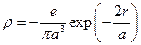 , где a – боровский радиус, а r – расстояние до протона, имеющего заряд e. Чему равна электростатическая энергия взаимодействия протона с электронным облаком.
, где a – боровский радиус, а r – расстояние до протона, имеющего заряд e. Чему равна электростатическая энергия взаимодействия протона с электронным облаком.
Ответ: 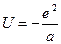
15. Вычислить дипольный момент равномерно заряженного полушара радиуса R, суммарный заряд полушара Q. Отрицательный заряд –Q, помещен на расстояние l от центра по оси симметрии.
Ответ: 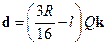
16.Определить дипольный и квадрупольный моменты системы, смещённой относительно начала координат на вектор c.
Решение:
с– вектор трансляции; 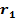 – точка, в которой рассчитываем момент;
– точка, в которой рассчитываем момент; 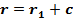 .
.
1) дипольный момент:
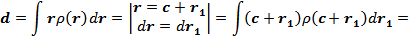
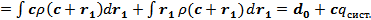
где 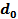 – дипольный момент системы, помещенной в начало координат.
– дипольный момент системы, помещенной в начало координат.
2) квадрупольный момент:
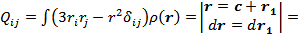
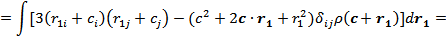
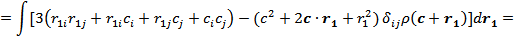
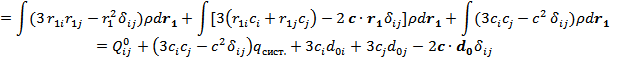
где 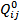 – квадрупольный момент системы, помещенной в начало координат
– квадрупольный момент системы, помещенной в начало координат
Ответ: 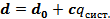 ;
;
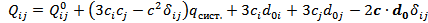 .
.
17.Внутри шара радиуса 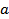 задан вектор плотности тока
задан вектор плотности тока 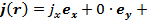
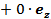 . Найти распределение векторного потенциала внутри и снаружи шара.
. Найти распределение векторного потенциала внутри и снаружи шара.
Решение:
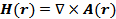 ,
,
откуда
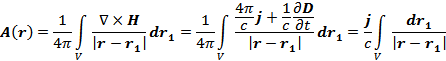
Соответственно ненулевой компонентой векторного потенциала будет только 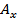 :
:
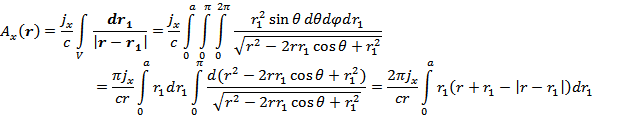
Рассмотрим область снаружи шара ( 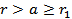 ):
):
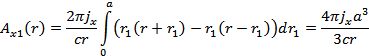
И рассмотрим область внутри шара ( 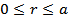 ):
):
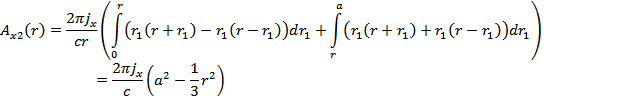
Заметим, что 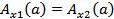 и
и 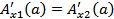 .
.
Окончательно получаем:
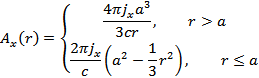
18 (А. 246).Заряд e совершает гармонические колебания вдоль оси X по закону 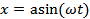 . Написать выражение для объемной плотности заряда
. Написать выражение для объемной плотности заряда 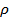 и объемной плотности тока
и объемной плотности тока 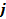 . Найти средние по времени за период
. Найти средние по времени за период 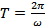 объемные плотности заряда
объемные плотности заряда 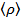 и тока
и тока 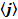 .
.
Решение:
По определению: 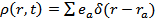 и
и 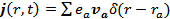
Следовательно:
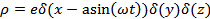
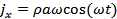 ;
; 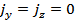
Найдем средние значения, как 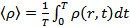 и
и 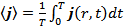
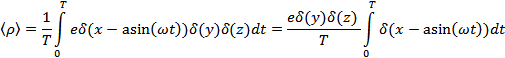
Используем свойство -функции: 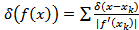 , где
, где 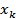 - нули функции
- нули функции 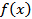 .
.
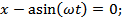
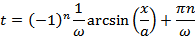
Интервалу от 0 до 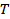 из всего множества корней принадлежат только 2:
из всего множества корней принадлежат только 2:
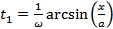 и
и 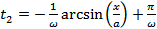
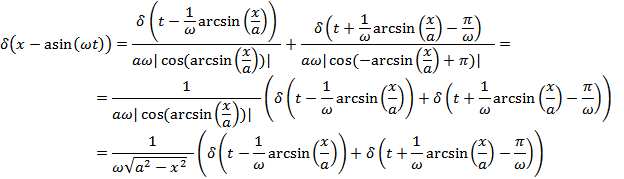
Возвращаясь к интегралу, получим:
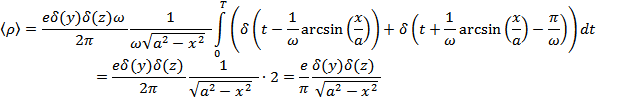
Это выражение справедливо при 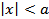 , т.к. в случае
, т.к. в случае 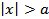 интеграл даст 0.
интеграл даст 0.
Аналогично показывается, что: 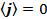
Ответ: 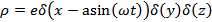 ;
;
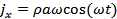 ;
; 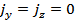 ;
;
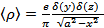 при
при 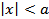 и
и 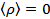 при
при 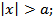
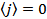
19 (А. 258). Радиус-вектор 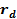 точки расположения диполя с моментов
точки расположения диполя с моментов 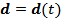 меняется во времени по закону
меняется во времени по закону 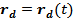 . Определить распределение объемных плотностей заряда и тока в пространстве. Вычислить магнитный момент
. Определить распределение объемных плотностей заряда и тока в пространстве. Вычислить магнитный момент 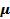 найденного тока
найденного тока
Решение:
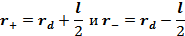
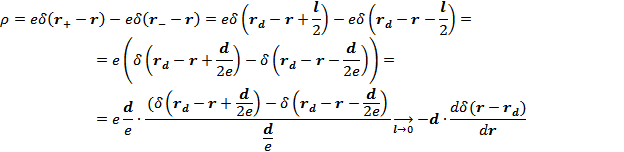
То есть 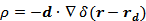
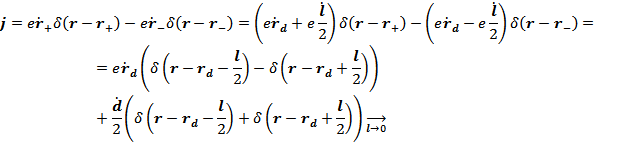
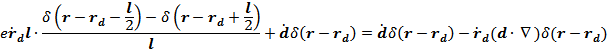
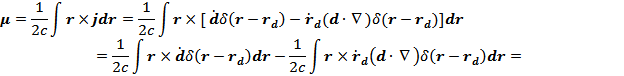
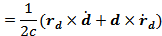
Ответ: 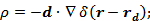
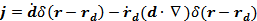 ;
;
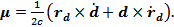
20 (А. 292).Простейшая линейная антенна представляет собой тонкий прямолинейный провод длины l, по которому течет ток  . Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока.
. Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока.
Решение:
 Пусть проводник соединяет две сферы Заряд каждой сферы
Пусть проводник соединяет две сферы Заряд каждой сферы
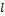
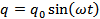 . В этом случае ток
. В этом случае ток 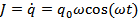 .
. 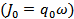 .
.
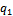
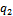 Таким образом, в целом, система представляет собой простейший диполь:
Таким образом, в целом, система представляет собой простейший диполь: 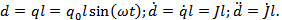 В результате интенсивность излучения такой системы равна:
В результате интенсивность излучения такой системы равна:
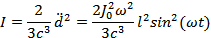
Интенсивность, усредненная за период колебаний тока 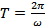 , равна:
, равна:
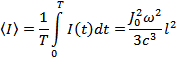
Ответ: 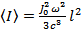 .
.
21 (А. 298).Протон с массой m и зарядом e движется перпендикулярно однородному постоянному магнитному полю с напряженностью 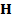 . Его кинетическая энергия в начальный момент времени
. Его кинетическая энергия в начальный момент времени 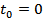 равнялась
равнялась 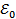 . Найти закон убывания кинетической энергии
. Найти закон убывания кинетической энергии 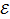 , обусловленный дипольным излучением.
, обусловленный дипольным излучением.
Решение:
Уравнение движения:
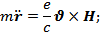
Т.к. поле направление перпендикулярно движению заряда, то 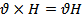
Тогда 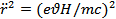 ;
; 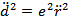
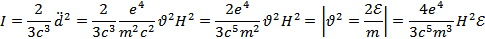
Интенсивность излучения - это энергия электромагнитного поля, излучаемая в единицу времени, т.е.
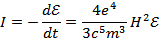
Решая это дифференциальное уравнение, находим закон убывания кинетической энергии:
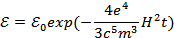
Ответ: 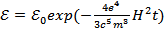 .
.
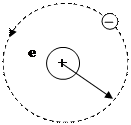
22 (А. 300).В классической модели атома, предложенной Резерфордом, электрон с зарядом e и массой m вращается по круговой орбите вокруг неподвижного ядра с зарядом Z|e|. Найти закон убывания полной энергии 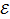 электрона, обусловленный дипольным излучением. Вычислить время
электрона, обусловленный дипольным излучением. Вычислить время 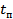 , по истечении которого электрон упадет на ядро вследствие потери энергии на дипольное излучение. В начальный момент времени
, по истечении которого электрон упадет на ядро вследствие потери энергии на дипольное излучение. В начальный момент времени 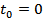 электрон находился на расстоянии R от ядра.
электрон находился на расстоянии R от ядра.
 Решение:
Решение:
Выразим интенсивность дипольного излучения через полную энергию электрона.
Воспользуемся теоремой о вириале: если частица движется в потенциальном поле с энергией 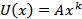 , то кинетическая энергия
, то кинетическая энергия 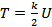 . Т.к. в данном случае потенциальная энергия электрона в поле ядра
. Т.к. в данном случае потенциальная энергия электрона в поле ядра 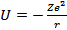 , то
, то
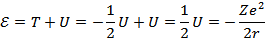
Следовательно, уравнение движения:
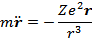
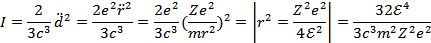
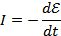
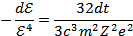
Решая дифференциальное уравнение, находим:
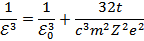
Где 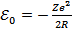
При падении частицы на центр 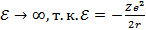
Таким образом:
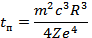
Ответ: 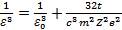 ;
;
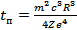 .
.
23 (А. 302).Доказать, что у замкнутой системы заряженных частиц с одинаковым отношением заряда к массе дипольное излучение отсутствует.
Решение:
Интенсивность дипольного излучения:
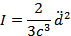
Закон движения: 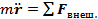
Дипольный момент системы точечных зарядов: 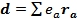
Таким образом:
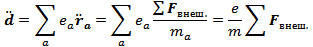
Поскольку система замкнутая, то векторная сумма внешних сил равная 0.
Следовательно 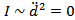
24 (А. 313).Простейшая рамочная антенна представляет собой прямоугольную рамку со сторонами a и b, по которым течет линейный ток  . Определить интенсивность I длинноволнового излучения антенны в среднем по времени за период колебаний тока.
. Определить интенсивность I длинноволнового излучения антенны в среднем по времени за период колебаний тока.
Решение:
По определению магнитный момент линейного тока:
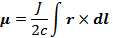
Так как 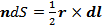 , то
, то 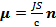 , где площадь сечения
, где площадь сечения 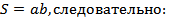
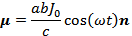
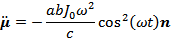
Отсюда интенсивность магнитно-дипольного излучения такой антенны равна:
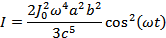
А интенсивность, усредненная за период колебаний:
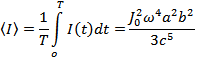
Ответ: 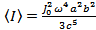 .
.
25 (А. 315).При каком условии интенсивность магнитно-дипольного излучения не зависит от выбора начала координат?
Решение:
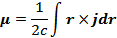
Если система транслирована относительно начала координат на вектор b,то заменяем 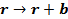 и для магнитного момента имеем:
и для магнитного момента имеем:
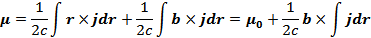
где 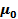 – магнитный момент системы в начале координат.
– магнитный момент системы в начале координат.
Воспользуемся соотношением из §65:
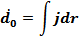
Где индекс 0 у дипольного момента означает, что он рассчитан в начале координат.
Интенсивность магнитно-дипольного излучения:
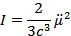
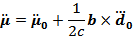
Таким образом, для того, чтобы интенсивность не зависела от выбора начала координат необходимо, чтобы выполнялось равенство 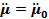 . Это реализуется в случае
. Это реализуется в случае 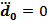
Ответ: 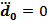 .
.
26 (А. 329).При каком условии интенсивность квадрупольного излучения не зависит от выбора начала координат?
Решение:
Квадрупольный момент системы, транслированной на вектор b (см. задачу 16):
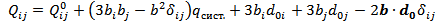
где 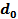 - дипольный момент системы в начале координат.
- дипольный момент системы в начале координат.
Интенсивность квадрупольного излучения:
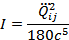
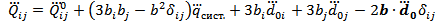
Таким образом, для того, чтобы интенсивность квадрупольного излучения не зависела от выбора начала координат необходимо, чтобы выполнялось равенство 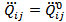 . Это реализуется в случае
. Это реализуется в случае 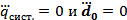 .
.
Ответ: 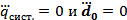 .
.
Список литературы.
Основная литература
1. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика:
а. Т.2. Теория поля. М, Наука, 1988, 1973. 530.1 (075.8) Л-222
б. Т.8. Электродинамика сплошных сред. М, Наука, 1992, 1982. 538.3 (075.8) Л-222
2. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М., Наука, 1990, 1979. 537.8 (075.8) В-493; 538.56 (075.8) В-493
3. Бредов М.М., Румянцев В.В., Топтыгин И.Н.Классическая электродинамика. М., Наука, 1985. 530.1 (075.8) Б-877
4. Галицкий В.М., Ермаченко В.М. Макроскопическая электродинамика. М., Высшая школа, 1988. 537.8 (075.8) Г-158
5. Алексеев А.И. Сборник задач по электродинамике, М., Наука, 1977.
Дополнительная литература
1. Батыгин В.В., Топтыгин И.Н. Сборник задач по электродинамике. М, Наука, 1970 г. 538.3 (076.1) Б-288
2. Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики. М., Наука, 1979
3. Гинзбург В.Л. Теоретическая физика и астрофизика. Дополнительные главы. М., Наука, 1987, 1981.
