Метод круглоцилиндрических поверхностей скольжения

Этот метод достаточно подробно рассмотрен в литературе и часто применяется на практике. Описание метода можно найти в книге Клейн Г.К. «Строительная механика сыпучих тел».

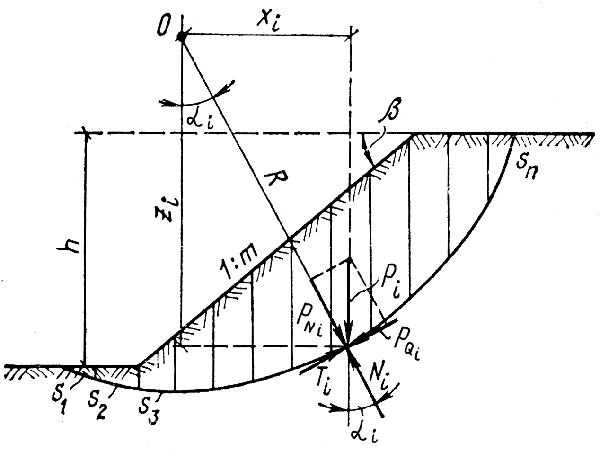
Рис.1. Схема расчета по методу круглоцилиндрических поверхностей скольжения.

Предполагаем, что центр O и радиус кривизны R поверхности скольжения заранее известны. В этом методе силы взаимодействия между соседними отсеками не учитываются, опираясь на то, что сумма этих сил должна быть равна нулю, а суммарный момент от них относительно точки O невелик. Касательная сила от всех нагрузок P_Qi=P_isin α_i является сдвигающей силой, вызывающей сползание откоса.
Сила сопротивления сдвигу сыпучего тела, находящегося за поверхностью скольжения (реакция), может быть представлена в виде суммы сил трения и сцепления:

T_i =N_i tanφ_i+ c_is_i,

где
N_i – нормальная реакция опоры.
s_i – длина дуги поверхности скольжения в пределах данного элемента i
φ_i – угол внутреннего трения в пределах дуги s_i
c_i – удельное сцепление в пределах дуги s_i.

Из уравнения проекций всех сил на нормаль к площадке отсека получаем.

N_i =P_Ni =P_i cosα_i,

Второе уравнение проекций остается неудовлетворенным, так как силы взаимодействия между отсеками не рассматривается. Условие равновесия откосов сводится к уравнению моментов всех сил, действующих на сползающую призму, относительно центра O поверхности скольжения.

Учет сейсмического воздействия при расчете противооползневых удерживающих конструкций осуществляется добавлением к расчетным усилиям, так называемой сейсмической силы Q_ci. Сейсмическая сила Q_ci приближенно определяется как доля от веса массы грунта, которая претерпевает сейсмическое воздействие:

Q_ci = μ*P_i

где
μ – коэффициент динамической сейсмичности, значения которого рекомендуется при расчете естественных склонов принимать по табл. 1. При расчете искусственных откосов (насыпи дорог, плотины т.д.) значения коэффициента из табл. 1 следует (приближенно) увеличивать в 1,5 раза.

Коэффициент динамической сейсмичности Таблица 1

Сейсмическая бальность района	1-6
μ	0.00	0.025	0.05	0.1	0.25	0.50	>0.75

Направление силы Q_ci рекомендуется считать наиболее неблагоприятным. В связи с этим будем принимать, что сейсмические силы в каждом отсеке оползневого блока направлены параллельно основанию отсека. Условие равновесия откосов сводится к уравнению моментов всех сил, действующих на сползающую призму, относительно центра O поверхности скольжения.

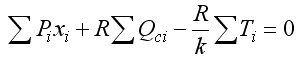
При этом силы сопротивления сдвигу уменьшены в k раз с учетом необходимости обеспечить определенный запас устойчивости откоса против разрушения.

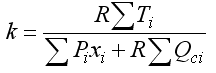
Тогда коэффициент выражается:

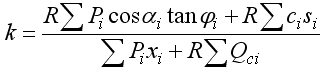
Учитывая, что 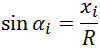, окончательно получим::

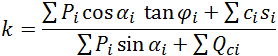
26.Когда устойчивость откоса требуемой крутизны не обеспечивается (см.п.4.5), то для его поддержания приходится устраивать подпорные стенки. Подпорные стенки широко применяются в промышленном, гражданском, дорожном, гидротехническом и других областях строительства.

Рассмотрим некоторые примеры подпорных стенок (рис.4.19):

- подпорная стенка как упор откоса грунта, равновесие которого невозможно без ограждения (рис.4.19,а);

- подпорная стенка как набережная (рис.4.19,б);

- подпорная стенка как ограждение подвального помещения здания (рис.4.19,в).

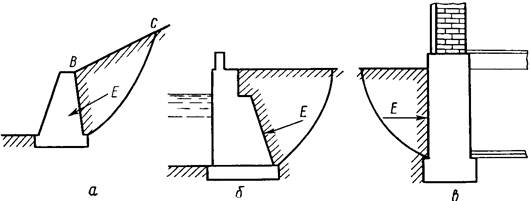Рис.4.19. Виды подпорных стенок

Подпорные стенки по конструктивному исполнению бывают массивные и тонкостенные (рис.4.20).

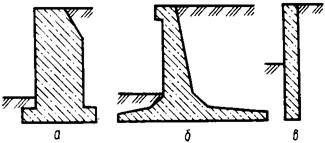
Рис.4.20. Конструкции подпорных стенок: а – массивная; б – тонкостенная; в – тонкостенная, заделанная в основание

Устойчивость массивных стенок на сдвиг и опрокидывание обеспечивается прежде всего их собственным весом, устойчивость тонкостенных конструкций – собственным весом стенки и грунта, вовлеченного в совместную работу, либо защемлением нижней части стенки в основание.

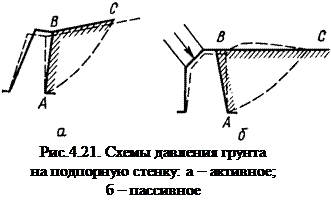Давление грунта стремится опрокинуть стенку вокруг ее переднего или заднего ребра (рис.4.21), причем подпорная стенка повернется (если основание податливое), как показано на рис.4.21 пунктиром.

При некоторой величине поворота стенки грунт за стенкой приходит в предельное напряженное состояние и в области грунта за подпорной стенкой возникают два сопряженных семейства криволинейных поверхностей скольжения. Перемещение грунта в предельном состоянии произойдет по некоторой поверхности АС, которая называется поверхностью скольжения, а призма АВС – призмой обрушения.

Если при этом подпорная стенка поворачивается по направлению от грунта, то будет иметь место активное давление грунта на стенку. Если же стенка повернется по направлению к грунту, то грунт засыпки будет выпирать вверх. Стенка будет преодолевать вес грунта призмы выпирания, что потребует значительно большего усилия, чем при активном давлении. Это пассивное давление.

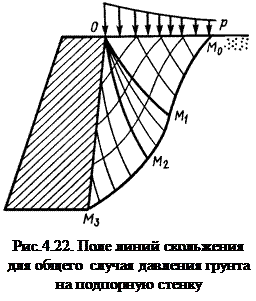
Для установления максимального давления грунта на подпорную стенку необходимо точно определить очертания линий скольжения в грунте за подпорной стенкой, что весьма сложно. Решение предложено проф. В.В.Соколовским. В треугольнике ОМ₀М₁ (рис.4.22) криволинейные линии скольжения переходят в систему взаимно пересекающихся прямых. В треугольниках ОМ₁М₂ и ОМ₂М₃ оба семейства линий скольжения криволинейны.

Для определения давления грунта на подпорные стенки принимают предложенный Ш.Кулоном упрощенный метод со следующими допущениями:

1) поверхность скольжения плоская;

2) призма обрушения соответствует максимальному давлению грунта на подпорную стенку.

Эти допущения применимы только для определения активного давления. Для пассивного давления этот метод дает недопустимые погрешности.

4.6.1. Аналитический метод определения давления грунта на подпорную стенку при допущении плоских поверхностей скольжения

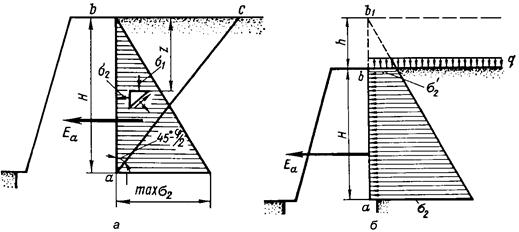Сыпучие грунты (с=0, j¹0). Рассмотрим условие предельного равновесия элементарной призмы, вырезанной из призмы обрушения вблизи задней грани абсолютно гладкой подпорной стенки при горизонтальной засыпке (рис.4.23,а). На горизонтальную и вертикальную площадки этой призмы при трении о стенку, равном нулю, будут действовать главные напряжения s₁и s₂.

Рис.4.23. Схема действия сил и эпюры давления сыпучего грунта для гладкой стенки (а) и при действии равномерно распределенной нагрузки и собственного веса грунта (б)

Из условия предельного равновесия

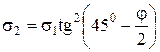(4.50)

или

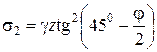. (4.51)

Следует отметить, что при повороте стенки к грунту будет возникать пассивное давление

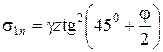. (4.52)

Равнодействующая активного давления грунта на подпорную стенку Е_а равна площади эпюры давления:

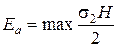
или

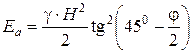. (4.53)

Она горизонтальна и приложена на одной трети высоты от низа подпорной стенки.

Учет равномерно распределенной нагрузки, приложенной к поверхности грунта (рис.4.23,б). Если к поверхности грунта приложена равномерно распределенная нагрузка q, то, заменив ее действием слоя грунта высотой h=q/g, получим точку b₁.

Найдем значение s₂ на глубине h и H+h:

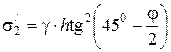, (4.54)

.

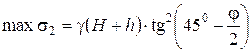На подпорную гладкую стенку будет действовать давление только трапецеидальной эпюры

или

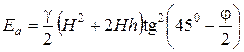. (4.55)

Учет наклона задней грани стенки (рис.4.24). Задняя грань подпорной стенки часто бывает наклонной. При этом угол наклона b может быть положительным (рис.4.24,а) или отрицательным (рис.4.24,б). Наклон стенки значительно влияет на величину активного давления. При положительном b активное давление будет больше, а при отрицательном – меньше по сравнению с давлением вертикальной задней грани стенки.

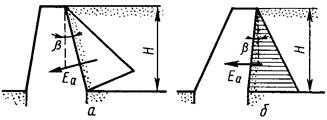
Рис.4.24. Подпорные стенки

с наклонной задней гранью

Активное давление определяется по формулам:

а) при положительном значении угла b

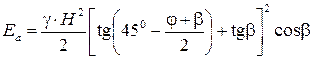; (4.56)

б) при отрицательном значении угла b

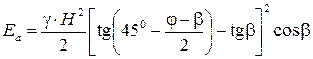. (4.57)

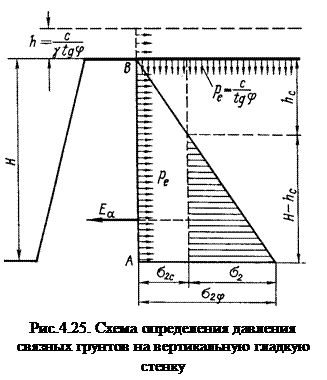
Связные грунты (j¹0 и с¹0). Определим давление связного грунта на вертикальную, абсолютно гладкую подпорную стенку при горизонтальной засыпке (рис.4.25). Действие сил сцепления заменяем всесторонним равномерным давлением связанности 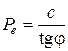. В этом случае горизонтальное напряжения

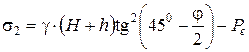. (4.58)

Учитывая, что 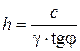и 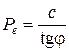, получим

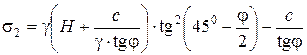. (4.59)

После преобразований формулу (4.59) можно записать так:

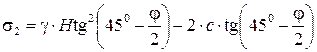(4.60)

или

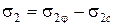, (4.61)

где

, .

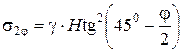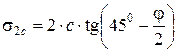Из приведенных данных видно, что сцепление грунта уменьшает боковое давление грунта на стенки на величину s_2с по всей высоте. На некоторой глубине h_с суммарное давление будет равно нулю. Найдя из условия s₂=0 глубину h_с, определим полное активное давление связного грунта на подпорную стенку как площадь треугольника со сторонами s₂ и H-h_с:

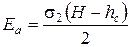. (4.62)

При h<H активное давление можно определить по формуле

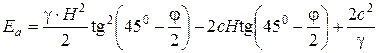, (4.63)

а пассивное давление

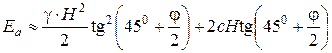. (4.64)

При учете сил трения, слоистости грунтов напластования, податливости стенки форма эпюр давления имеет сложный вид, направление равнодействующей будет наклонным. Так, например, на рис.4.26 показано направление равнодействующей активного давления при учете сил трения грунта о заднюю стенку.

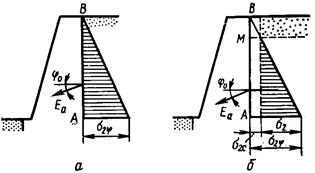
Рис.4.26. Эпюры давления грунта на подпорные стенки с учетом сил трения для сыпучего (а) и связного (б) грунтов

(j₀ – угол трения грунта о стенку)

4.6.2. Определение давления грунтов на подпорные стенки по методам теории предельного равновесия

Строгое решение задачи давления грунтов на подпорные стенки получено В.В.Соколовским на основании решения дифференциальных уравнений предельного состояния грунтов и условия предельного равновесия.

Активное давление грунта на стенку вычисляют по формуле

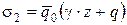. (4.65)

Пассивное давление

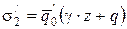. (4.66)

Значения 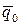и 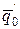табулированы в зависимости от угла внутреннего трения грунта j, а также угла трения грунта о стенку j₀, угла, составляемого давлением грунта с нормалью к задней грани стенки d и угла, составляемого задней гранью стенки с горизонтом q (табл.III.7, III.8 приложения III).

4.6.3. Графический метод определения давления грунтов на подпорные стенки

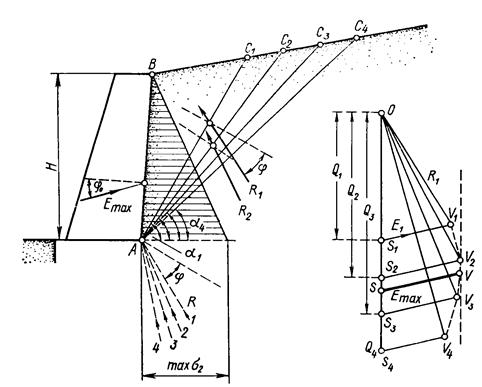
Рис.4.27. Графическое определение максимального давления грунта

на подпорную стенку

Для нахождения максимального давления на подпорную стенку АВ (рис.4.27) проводим несколько возможных плоскостей скольжения АС₁, АС₂, АС₃, АС₄. Для этих поверхностей скольжения при a₁, a₂, a₃, a₄ направления реактивных сил R₁, R₂, R₃, R₄будут различными, отклоняясь от вертикали под углом a₁-j, a₂-j, a₃-j, a₄-j, а направления реактивных сил Е -одинаковыми.

Зная направления сил, строим совмещенно силовые треугольники. Для этого из точки О откладываем значения сил Q₁, Q₂, Q₃, Q₄и проводим лучи по направлениям реактивных силR₁, R₂, R₃, R₄. Затем из точек Q₁, Q₂, Q₃, Q₄строим лучи параллельно действию сил Е и получаем соответственно точки пересечения каждой пары лучей V₁, V₂, V₃, V₄. Через эти точки проводим плавную кривую и к ней вертикальную касательную. Из точки касания V проводим линию, параллельную действию сил Е. Отрезок QV в масштабе сил и будет активным давлением Е_а на подпорную стенку.

Анализ экспериментальных и теоретических данных давления грунта на подпорные стенки показывает, что вопрос давления грунтов на подпорные стенки значительно сложней, чем это вытекает из рассмотрения частных теоретических решений. Большое значение имеют перемещения стенки, свойства грунтов засыпки, шероховатость стенки и другие допущения, положенные в основу теоретических методов расчета. Например, перемещение подпорной стенки на 0,2 мм может в 3 раза снизить величину активного давления Е_а.

При определении активного давления грунтов на массивные подпорные стенки можно с полным основанием применять методы расчета, основанные на допущении плоских поверхностей скольжения, для пассивных давлений при этом допущении величина отпора грунта будет значительно преувеличена. В этих случаях нужно применять точные методы расчета.