Интервальная оценка параметров генеральной совокупности

Точечные оценки параметров распределения не дают информации о степени близости к соответствующему теоретическому параметру. Поэтому построение интервала, в котором с заданной степенью достоверности будет находиться оцениваемый параметр, является более информативным способом оценивания неизвестных параметров.

Интервальная оценка – это числовой интервал, который определяется двумя числами-границами интервала, содержащий неизвестный параметр генеральной совокупности.

Доверительный интервал – это интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность р - это такая вероятность, что событие вероятности (1 - р) можно считать невозможным. - это уровень значимости. (Обозначения могут быть любыми, часто обозначают наоборот). Обычно в качестве доверительных вероятностей используют вероятности, близкие к 1. Тогда событие, что интервал накроет характеристику, будет практически достоверным. Это

Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей. Обычно указывают 95% доверительный интервал.

Для выборки малого объема (n< 30) нормально распределенного количественного признака х доверительный интервал может иметь вид:

где | - генеральное среднее; 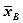- выборочное среднее; t - нормированный показатель распределения Стъюдента с (n - 1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал. Термин «степени свободы» означает, что их можно вычислить как объем выборки минус число ограничиваю­щих условий; — ошибка выборочной средней.

Для интерпретации доверительного интервала в клинических работах следует помнить, что ширина доверительного интервала зависит от ошибки выборочной средней, которая в свою очередь зависит от объема выборки (n) и от изменчивости данных (S). Если выборка небольшая, то доверительный интервал более широкий, чем в случае выборки большого объема. Широкий доверительный интервал указывает на неточную оценку, а узкий – на точную оценку.

Верхний и нижние пределы доверительного интервала показывают, будут ли результаты клинически значимы.

Количественный признак х генеральной совокупности распределен нормально. По выборке объема n = 16 найдены выборочная средняя 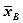= 20,2 и среднее квадратическое отклонение S = 0,8. Определить неизвестное математическое ожидание при помощи доверительного интервала при .

Решение:

Найдем t из таблицы распределения Стъюдента при уровне значимости и числе степеней свободы f=n-1; f=16-1=15.

Запишем:

Имеется выборка объёма n=11 - это значения систолического давления у мужчин в начальной стадии шока,

х: 127,124,155,129,77,147,65,109,145,141.

С помощью пакета прикладных программ на ЭВМ провести статистическую обработку данных выборки и определить доверительный интервал для генеральной средней при

Решение:

Пусть расчет на ЭВМ дал: выборочное среднее

По таблице распределения Стьюдента найдем:

Из обследованных 430 случайно выбранных колосьев пшеницы 37 оказались пораженными головней. Каковы 95%-ные доверительные границы процента пораженности для данного поля?

Решение:

Выборочный средний процент пораженности составляет:

Теперь по формуле находим:

.

Тогда для 95%-ного доверительного уровня имеем доверительные границы:

,

т. е . 95%-ный доверительный интервал есть (6,0 2)%.

При рентгеновском облучении 10 мышей дозой в 550 Р погибло 5 мышей. Каковы 99%-ные доверительные границы для доли мышей, погибающих пол действием данной дозы облучения?

Решение:

Имеем:

.

поэтому при Р=99% (и ) доверительные границы будут:

0,5-2,58*=0,5-0,408=0,092=9,2%,

0,5+2,58*0,158=0,5+0,408=0,908=90,8% .

Так как найденный доверительный интервал перекрывает почти весь возможный диапазон расположения истинной доли погибающих мышей (от 0 до 100%), то следует заключить, что опыт вообще не дал почти никакого результата (кроме указания, что при данной дозе облучения выборка из 10 мышей недостаточно велика для нахождения ответа на поставленный вопрос).

При изучении в 10 опытах образования у собаки условного рефлекса под действием ранее индифферентного раздражителя были получены результаты (время между моментом включения условного раздражителя и моментом начала слюноотделения): с, с. Надо найти 95% -ный доверительный интервал для µ , характеризующий данное животное.

Решение:

Для Р=95% и f=n-1=9(число степеней свободы дисперсии) находим в приложении значение t=2,26. Поэтому границы доверительного интервала будут:

Результаты обычно записываются в одной из следующих двух форм:

или

Из табл. приложений видно, что значения зависят особенно резко от f при малых f. Поэтому увеличение малых n приводит к сужению доверительного интервала определяемого величиной не только за счет уменьшения множителя , но в еще большей степени за счет уменьшения . Так, при изменении n с двух опытов до трех уменьшает множитель с до , т.е. доверительный интервал сужается в 9,0 : 2,5 = 3,6 раза; при Р=99% ширина доверительного интервала уменьшается даже примерно в 8 раз ( ; ). При больших значениях n увеличение n на одну единицу сказывается на ширине доверительного интервала гораздо меньше.

Из генеральной совокупности извлечена выборка объема n=10:

вариант xi -2 1 2 3 4 5

частота ni 2 1 2 2 2 1

Оценить с надежностью 0,95 математическое ожидание a нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интеграла.

Решение:

Выборочную среднюю и исправленное среднее квадратическое отклонение найдем соответственно по формулам:

Подставим в эти формулы данные задачи, получим

Найдем . Пользуясь таблицей, по g=0,95 и n=10 находим =2,26.

Найдем искомый доверительный интервал

.

Подставляя получим искомый доверительный интервал 0,3<a<3,7, покрывающий неизвестное математическое ожидание a с надежностью 0,95.

По данным 9 независимых равноточных измерений некоторые физические величины найдены среднее арифметическое результатов измерений и исправленное квадратическое отклонение S=6. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью g=0,99.

Решение:

Истинное значение измеряемой величины равно ее математическому ожиданию a. Поэтому задача сводится к оценке математического ожидания (при неизвестном s) при помощи доверительного интервала

Здесь все величины, кроме tg, известны. Найдем tg. По таблице g=0,95 и n=9 находим tg=3,36.

Подставим =30,1, tg=3,36, S=6, n=9, получим искомый интервал

23,38<a<36,82

По данным выборки объема n=16 из генеральной совокупности найдено исправленное среднее квадратическое отклонение s=1 нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение s с надежностью 0,95.

Решение:

Задача сводится к отысканию доверительного интервала

S(1-q)<s<s(1+q), (если q<1) (*)

или 0<s<s(1+q) (если q>1).

По данным g=0,95 и n=16 найдем q=0,44. Так как q<1, то, подставив s=1, q=0,44 в соотношение (*), получим искомый доверительный интервал 0,56<s<1,44.

Варианты заданий

№ 13.1. При исследовании частоты дыхания по выборке объема n = 15 были получены выборочная средняя 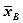=18,5 и среднее квадратическое отклонение S = 0,6. Определить интервальную оценку математического ожидания с вероятностью .

№ 13.2. Найти доверительный интервал для оценки с уровнем доверительной вероятности неизвестного математического ожидания нормального распределения признака х – диаметра эритроцита – генеральной совокупности, если выборочная средняя 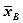=10,2 мкм; ис­правленное выборочное среднее квадратическое отклонение S = 4 и объем выборки п = 16. 16. При исследовании эффективности диуретика было уста­новлено, что среднее увеличение диуреза в группе из n=10 человек составило . Найти доверительный интервал ( ) для среднего изменения диуреза, если ошибка выборочной средней .

№ 13.3. При исследовании проницаемости сосудов сетчатки для выборки объемом n = 25 были получены следующие данные: выборочная средняя 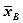= 14, среднее квадратическое отклонение S=5. Считая, что данный признак х распределен нормально, найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания.

№ 13.4. Определить доверительный интервал для средней активности препарата с уровнем доверительной вероятности .

х: 905,925,940,961,974, 995.

№ 13.5. С доверительной вероятностью определить для количества крови, протекающего за 1 минуту через почки, если выборочная средняя 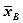= 1300мл крови, а ошибка выборочной средней =30 мл. Объем выборки n = 12.

Контрольные вопросы

1. Перечислить основные понятия математической статистики.

2. Каким образом строится полигон частот и гистограмма.

3. Что называют вариантой, вариационным рядом и относительной частотой.

4. Перечислить формы вариационного ряда.

5. Перечислить статистические оценки параметров распределения.

6. Определение статистической оценки неизвестного параметра.

7. Какая оценка называется точечной?

8. Каким требованиям должны удовлетворять статистические оценки?

9. Сформулировать определения генеральной средней и генеральной дисперсии.

10. Записать выражения для вычисления выборочной средней, выборочной дисперсии и исправленной дисперсии. Какая из этих оценок не является несмещенной?

11. Методики вычисления границ доверительного интервала для оценки математического ожидания нормально распределенной СВ при известном и неизвестном s.

12. Методика вычисления границ доверительного интервала для оценки среднего квадратического отклонения нормально распределенной СВ.