Коэффициенты ассоциации и контингенции

Коэффициенты ассоциации и контингенции применяются тогда, когда исследуется связь между варьированием двух атрибутивных признаков, по каждому признаку имеется две группы (таблица 10.2).

Таблица 10.2 – Варьируемые атрибутивные признаки

			Всего
	a	b	a+b
	c	d	c+d
Итого	a+c	b+d	a+b+c+d

Коэффициент ассоциации вычисляется по формуле

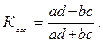
Коэффициент контингенции вычисляется

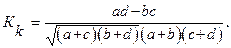
Коэффициенты контингенции и ассоциации принимают значение от -1 до 1, показывают не только тесноту, но и направление связи.

Если коэффициент >0, связь прямая, <0 – обратная. Чем ближе коэффициент к ±1, тем связь теснее.

Коэффициент контингенции всегда меньше коэффициента ассоциации. Он дает более осторожную оценку тесноты связи.

Измерение тесноты связи между количественными признаками

Методы измерения связи между количественными признаками не могут обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических(корреляционных и дисперсионных).

Метод сравнения параллельных рядов

Установить наличие и характер связи между количественными признаками можно с помощью метода сравнения параллельных рядов, заключающегося в следующем.

Признаки-факторы мы располагаем в возрастающем или убывающем порядке в зависимости от целей исследования и рядом записываем соответствующий результативный признак. Затем путем сопоставления двух параллельных рядов делаем предположение о наличии связи и ее направлении.

Пример: Находим зависимость между производительностью труда (у) и энерговооруженностью (х), имея данные по 25-и заводам.

№ завода	Х	У	Знаки отклонений	Ранги	Разность рангов
Х	У	Х	У	│d│	d2
	6,0		-	-		1,5	0,5	0,25
	6,1		-	-		3,5	1,5	2,25
	6,8		-	-		10,5	7,5	56,25
	7,2		-	-		5,5	1,5	2,25
	7,4		-	-		1,5	3,5	12,25
	7,9		-	-		3,5	2,5	6,25
	8,2		-	-		5,5	1,5	2,25
	8,5		-	-		7,5	0,5	0,25
	8,6		-	-		10,5	1,5	2,25
	9,1		-	+		17,5	7,5	56,25
	9,4		-	-		7,5	3,5	12,25
	9,9		-	+		14,0	2,0	4,00
	10,5		+	+		14,0	1,0	1,00
	11,2		+	+		17,5	3,5	12,25
	11,3		+	-		10,5	4,5	20,25
	11,5		+	+		21,5	5,5	30,25
	11,7		+	+		21,5	4,5	20,25
	12,1		+	+		17,5	0,5	0,25
	12,3		+	+		14,0	5,0	25,00
	12,6		+	+		17,5	2,5	6,25
	12,7		+	+		21,5	0,5	0,25
	12,9		+	-		10,5	11,5	132,25
	13,0		+	+		24,5	1,5	2,25
	13,2		+	+		21,5	2,5	6,25
	13,3		+	+		24,5	0,5	0,25
Итого:	253,7		–	–	–	–	–	413,50

Коэффициент Фехнера

Коэффициент Фехнера основан на методе параллельных рядов. Суть его в том, что сравниваются знаки отклонений значений признака от их средних арифметических.

1) Находим средние арифметические

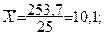
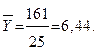
2) Рассмотрим совпадение и несовпадение знаков отклонений.

Совпадение знаков (С) означает согласованную вариацию, а несовпадение (Н)- нарушение этой согласованности.

С=21,

Н=4.

Коэффициент Фехнера вычисляется по формуле

.

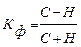Принимает значения от –1до +1.

Вычисляем:

.

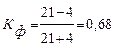Связь прямая и заметно согласованная.

Коэффициент Фехнера примитивен, т.к. улавливает только направление связи и не учитывает ее величину.