Показательные и логарифмические неравенства
Экспресс – курс подготовки
К ЕГЭ по математике
Вашему вниманию предложены следующие темы:
- Преобразования степенных, иррациональных и логарифмических выражений.
- Иррациональные, показательные и логарифмические уравнения.
- Показательные и логарифмические неравенства.
- Дробно-рациональные неравенства (метод интервалов).
Весь необходимый материал изложен кратко и просто. Все теоретические вопросы сопровождаются разобранными примерными заданиями ЕГЭ по математике. Задания на экзамене будут сформулированы, может быть, иначе, но решаться они будут по подобным алгоритмам и по тем же формулам.
Желаем успешной сдачи экзамена!
Степенные выражения
| Определения и свойства степени | Примеры |
Определения: 1) a 1 = а (а 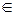 R) 2) аn = а ∙ а ∙... a (а R) 2) аn = а ∙ а ∙... a (а 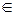 R, n R, n 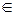 N, n N, n 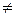 0) 3) а 0=1 (а 0) 3) а 0=1 (а 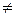 0, а 0, а 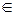 R) 4) а -n = R) 4) а -n = 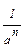 (а (а 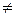 0, а 0, а 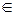 с R, n с R, n 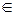 N) 5) N) 5) 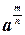 = = 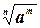 (n (n 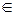 N, m N, m 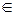 Q, а >0) Q, а >0) | (-1,7в)1 = -1,7в (-1,7в)3 = (-1,7в) (-1,7в) (-1,7в) = -4,913 (—1,7 в)0=1, если в 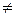 0 (—0,25) -3 = 0 (—0,25) -3 = 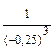 = (-4)3 = 64 = (-4)3 = 64 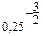 = = 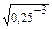 = = 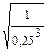 = = 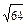 = 8 = 8 |
| Свойства: | Примеры |
| m1,5 ∙ m-2 = m1,5+(-2)= m-0,5 l,53х.1,5 -0,5х= 1,52,5х 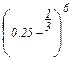 =(0,25)-2 = 42 = 16 (5х)2 = 52х = (52)х = 25х m1,5 : m-2 = m1,5-(-2)= m3,5 l,53х : 1,5 -0,5х= 1,53,5х 32х · 52х = (3∙5)2х =152х =(0,25)-2 = 42 = 16 (5х)2 = 52х = (52)х = 25х m1,5 : m-2 = m1,5-(-2)= m3,5 l,53х : 1,5 -0,5х= 1,53,5х 32х · 52х = (3∙5)2х =152х 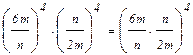 =34=81 =34=81 |
| Свойства арифметических корней n-степени | Примеры |
1) Если а 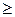 0, b≥0. то 0, b≥0. то 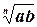 = = 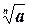 · · 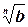 | 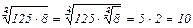 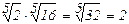 |
2) Если а 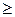 0, b>0. то 0, b>0. то 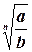 =· =· 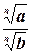 | 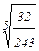 = = 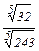 = = 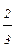 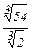 = = 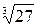 =3 =3 |
3) Если а 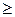 0, n 0, n 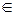 N, k N, k 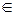 N, то N, то 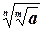 = = 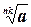 | 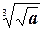 -3 -3 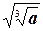 = = 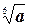 -3 -3 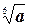 =-2 =-2 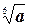 |
4) Если а 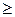 0, n 0, n 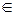 N, k N, k 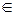 N, то N, то 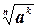 = = 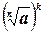 | 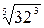 = = 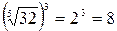 |
5) Если а 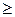 0, n 0, n 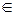 N, k N, k 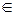 N, то N, то 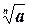 = = 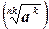 | 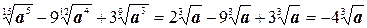 |
Преобразования степенных и иррациональных выражений
Пример 1. Вычислите: 4∙ 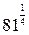 + 0,50.
+ 0,50.
Решение.
Первый способ. Используя определения степени с нулевым и дробным показателями, получаем: 4∙ 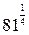 + 0,50 =4·
+ 0,50 =4· 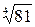 +1 = 4∙3+1= 13.
+1 = 4∙3+1= 13.
Второй способ. Используя определения степени с натуральным и нулевым показателями и свойства степеней, получаем: 4∙ 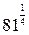 + 0,50 =4∙
+ 0,50 =4∙ 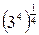 +1= 4∙
+1= 4∙ 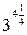 + 1 = 4∙3+1= 13
+ 1 = 4∙3+1= 13
Ответ 13.
Пример 2. Найдите значение выражения 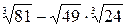 .
.
Решение. Учитывая, что 81 = 27·3, а 24 = 8·3, и используя формулу 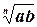 =
= 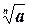 ·
· 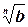 , получим:
, получим: 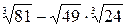 =
= 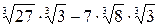 = 3
= 3 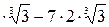 =3
=3 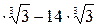 =
= 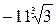
Ответ: 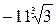 .
.
Пример 3. Упростите выражение 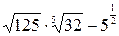 .
.
Решение. 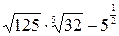 =
= 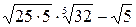 =
= 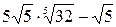 =
= 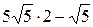 =
= 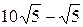 =
= 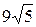
Ответ: 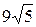
Пример 4. Выполните действия: ( 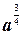 )2
)2 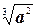 .
.
Решение. Используя определение степени с дробным показателем 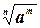 =
= 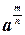 (n
(n 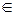 N, m
N, m 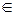 Q, а >0), а также свойства степеней (ах)у = аху, ах · ау = ах+у, получаем:
Q, а >0), а также свойства степеней (ах)у = аху, ах · ау = ах+у, получаем:
( 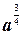 )2
)2 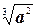 =
= 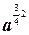 ·
· 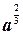 =
= 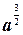 ·
· 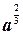 =
= 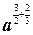 =
= 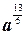
Ответ: 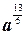
Пример 5. Выполните действия: 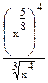
Решение. 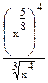 =
= 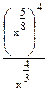 =
= 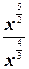 =
= 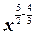 =
= 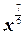
Ответ: 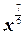 .
.
Пример 6. Упростите выражение 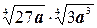
Решение. 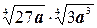 =
= 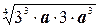 =
= 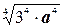 =
= 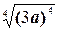 =3а
=3а
Ответ:3а.
Иррациональные уравнения
Иррациональные уравнения, встречающиеся на экзамене, чаще всего решаются методом возведения в степень, которую имеет корень, содержащий неизвестное, или заменой неизвестного. Не следует забывать, что в степень возводятся обе части уравнения.
Так как при возведении в степень обеих частей уравнения новое, получившееся после
этой операции уравнение, не всегда равносильно искомому, то нужно либо делать проверку, либо с самого начала выписывать неравенства, задающие область допустимых значений неизвестной величины. При осуществлении проверки значение неизвестной являющееся решением необходимо подставлять только в первоначальное уpaвнение, а не в какие-то промежуточные.
Рассмотрим применение некоторых методов решения иррациональных уравнений.
Пример 1. Решите уравнение 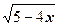 = 2х + 5.
= 2х + 5.
Решение. Возведем исходное уравнение 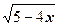 = 2х + 5 в степень, равную показателю корня (
= 2х + 5 в степень, равную показателю корня ( 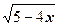 )2 = (2х + 5)2 5 - 4х =4х2+ 20х+25 4х2 + 24х + 20 = 0;
)2 = (2х + 5)2 5 - 4х =4х2+ 20х+25 4х2 + 24х + 20 = 0;
х2 + 6х + 5 = 0; х = -5 или х = -1.
Проверка. х = -5: 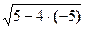 = 2·(-5) + 4
= 2·(-5) + 4
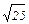 = -5
= -5
Это неверное числовое равенство, значит, число -5 не является корнем данного уравнения.
х = - 1: 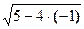 = 2·(-1) + 4
= 2·(-1) + 4
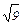 = 3
= 3
Это верное числовое равенство, значит, число -1 является корнем данного уравнения.
Показательные и логарифмические неравенства
Пример 2. Решите неравенство 4х ≥ 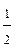
Решение. Так как 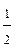 = 2-1 и 4х = 22х, то исходное неравенство равносильно неравенству 22х≥2-1 . Функция у = 2х возрастающая, т, к. 2 > 1. Поэтому полученное неравенство, а значит, и исходное, равносильно неравенству 2х ≥ -1, то есть х ≥ -0,5.
= 2-1 и 4х = 22х, то исходное неравенство равносильно неравенству 22х≥2-1 . Функция у = 2х возрастающая, т, к. 2 > 1. Поэтому полученное неравенство, а значит, и исходное, равносильно неравенству 2х ≥ -1, то есть х ≥ -0,5.
Ответ: 3.
Пример 3. Найдите число целых отрицательных решений неравенства 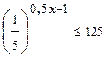 .
.
Решение. Неравенство 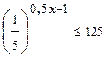 равносильно неравенству
равносильно неравенству 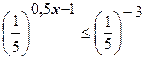
Поскольку 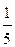 <1, то функция у =
<1, то функция у = 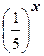 убывает, поэтому исходное неравенство равносильно неравенству 0.5х - 1
убывает, поэтому исходное неравенство равносильно неравенству 0.5х - 1 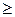 -3. Отсюда получаем х
-3. Отсюда получаем х 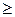 -4. Целыми отрицательными решениями неравенства являются четыре числа: -4, -3, -2, -1.
-4. Целыми отрицательными решениями неравенства являются четыре числа: -4, -3, -2, -1.
Ответ:4.
Пример 4. Найдите число целых решений неравенства lоg 0,5(х - 2) 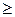 -2.
-2.
Решение. Запишем правую часть неравенства как произведение -2 ∙1 и воспользуемся тождеством 1 = lоgbа, при условии а = 0,5.
Получим:
1оg0,5(х - 2) 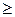 -2. 1; 1оg 0,5(х - 2)
-2. 1; 1оg 0,5(х - 2) 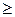 -2 1оg 0,5 0,5;
-2 1оg 0,5 0,5;
1оg0,5(х - 2) 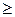 1оg 0,5 0,5-2 ; 1оg 0,5(х - 2)
1оg 0,5 0,5-2 ; 1оg 0,5(х - 2) 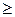 lоg 0,5 4.
lоg 0,5 4.
Поскольку 0,5 < 1, то функция у = 1оg 0,5х убывающая, поэтому полученное неравенство, а значит, и исходное неравенство, равносильно неравенству 0 < х-2 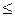 4 (условие 0 < х - 2 получено с учетом области определении логарифмической функции).
4 (условие 0 < х - 2 получено с учетом области определении логарифмической функции).
Отсюда получаем 2 < х 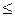 6. Следовательно, х принимает 4 целых значения: 3; 4; 5; 6.
6. Следовательно, х принимает 4 целых значения: 3; 4; 5; 6.
Ответ: 4.
Пример 5. Решите неравенство ln (х- 1) < ln (3х+ 2).
Решение. Т. к. е > 1, то функция у = ln х возрастающая, следовательно, данному неравенству равносильна система неравенств
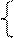
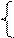 х - 1 < 3х+2, 2х > -3 х >1,5
х - 1 < 3х+2, 2х > -3 х >1,5
х - 1 > 0 х > 1 х >1
Итак, решения неравенства составляют интервал (1;+ 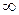 )
)
Ответ: ( 1 ; + 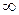 )
)
Дробно-рациональные неравенства (метод интервалов)
Пример 6. Решите неравенство 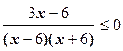
Решение. Найдем значения переменной, при которых дробь равна нулю: 3х — 6 = 0, х =2. Найдем значения переменной, при которых дробь не имеет смысла: (х — 6) (х + 6) = 0,
х = 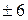 . Отметим на координатной прямой найденные числа:
. Отметим на координатной прямой найденные числа:

-6 2 6 х
На каждом из получившихся промежутков определим знак значений дроби:
при х = 7 имеем 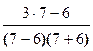 > 0; при х = 5 имеем
> 0; при х = 5 имеем 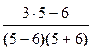 < 0
< 0
при х = 0 имеем 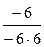 > 0; при х = -7 имеем
> 0; при х = -7 имеем 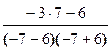 < 0.
< 0.
Отметим эти данные на рисунке
- + - +
 -6 2 6 х
-6 2 6 х
Дробь принимает неположительные значения на промежутках ( - 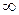 ;-6 )
;-6 ) 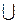 [ 2 ; 6 ]
[ 2 ; 6 ]
Ответ: ( - 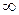 ;-6 )
;-6 ) 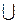 [ 2 ; 6 ]
[ 2 ; 6 ]
Пример 7. Вычислите сумму всех натуральных решений неравенства 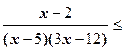 0
0
Решение. х - 2 = 0, х = 2
(х - 5)(3х -12) = 0, х =5 или х = 4
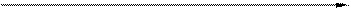
2 4 5 х
На крайнем правом промежутке дробь принимает положительные значения, т. к. 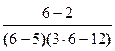 > 0. совпадающих корней у числителя и знаменателя дроби нет, значит, на полученных промежутках знаки чередуются (см. рис.).
> 0. совпадающих корней у числителя и знаменателя дроби нет, значит, на полученных промежутках знаки чередуются (см. рис.).
 - + - +
- + - +
2 4 5 х
Решением неравенства будет объединение промежутков (- 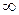 ;2]
;2] 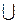 (4;5). На этих промежутках находятся два натуральных сила 1 и 2. Сумма этих чисел 1 + 2 = 3
(4;5). На этих промежутках находятся два натуральных сила 1 и 2. Сумма этих чисел 1 + 2 = 3
Ответ: 3.
