Задачи для самостоятельного решения. 4.1. Найти момент инерции тонкого однородного стержня длиной l=30 см и массой m=100 г относительно оси
4.1. Найти момент инерции тонкого однородного стержня длиной l=30 см и массой m=100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины.
[Ответ: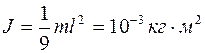 
.]
4.2. Вычислить момент инерции медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина b=2 мм и радиус R=100 мм.
[Ответ: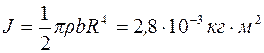 
.]
4.3. Три маленьких шарика массой m=10 г каждый расположены в вершинах равностороннего треугольника со стороной а=20 см и скреплены между собой. Определить момент инерции J системы относительно оси: 1) перпендикулярной плоскости треугольника и проходящей через центр описанной окружности; 2) лежащей в плоскости треугольника и проходящей через центр описанной окружности и одну из вершин треугольника. Массой стержней, соединяющих шары, пренебречь.
[Ответ: 1)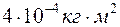 
; 2) 
.]
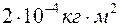4.4.Вычислить момент инерции J проволочного прямоугольника со сторонами а=12 см и b=16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ=0,1 кг/м.
[Ответ: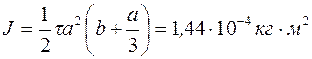 
.]
4.5. Два однородных тонких стержня: AB длиной l1=40 см и массой m1=900 г и CD длиной l2=40 см и массой m2=400 г скреплены под прямым углом (рис.4.7). Определить момент инерцииJ системы стержней относительно оси ОО/, проходящей через конец стержня AB параллельно стержню CD.
[Ответ: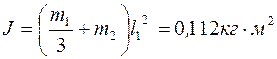 
.]
4.6. Показать, что для тонкой пластинки произвольной формы имеется следующая связь между моментами инерции: J1+J2=J3, где 1, 2, 3 – три взаимно перпендикулярные оси, проходящие через одну точку, причем оси 1 и 2 лежат в плоскости пластинки. Используя эту связь, найти момент инерции тонкого круглого однородного диска радиуса R и массы m относительно оси, совпадающей с одним из его диаметров.
[Ответ: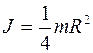 
]
4.7. Определить момент инерции J проволочного равностороннего треугольника со стороной a=10 см относительно: 1) оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине (рис. 4.8, а); 2) оси, совпадающей с одной из сторон треугольника (рис. 4.8, б). Масса m треугольника равна 12 г и равномерно распределена по длине проволоки.
[Ответ: 1)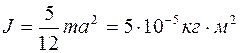 
; 2)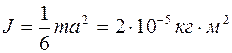 
.]
4.8. Исходя из формулы для момента инерции однородного шара, найти момент инерции тонкого сферического слоя массы m и радиуса R относительно оси, проходящей через его центр.
[Ответ: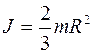 
]
 |
4.9. Однородный диск радиуса
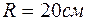имеет круглый вырез как показано на рис.4.9. Масса оставшейся (заштрихованной) части диска 
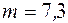кг. Найти момент инерции такого диска относительно оси С, проходящей через его центр инерции и перпендикулярной к плоскости диска.
|
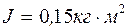] 4.10. Концы тонких нитей, плотно намотанных на ось радиуса r диска Максвелла, прикреплены к горизонтальной штанге. Когда диск раскручивается, штангу поднимают так, что диск остается неизменно на одной и той же высоте. Масса диска с осью m, момент инерции прибора относительно его оси J. Найти натяжение T каждой нити и ускорение a штанги.
[Ответ: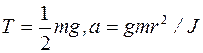 
.]
4.11. Тонкий однородный стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент M.
[Ответ: 0,025 Н∙м.]
4.12. На горизонтальную ось насажаны маховик и легкий шкив радиусом R=5 см. На шкив намотан шнур, к которому привязан груз массой m=0,4 кг. Опускаясь равноускоренно, груз прошел путь S=1,8 м за время t=3 c. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.
[Ответ: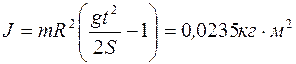 
]
4.13. Вал массой m=100 кг и радиусом R=5 см вращался с частотой n=8 c-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40 H, под действием которой вал остановился через t=10 с. Определить коэффициент трения μ.
[Ответ: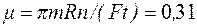 
]
4.14. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение a оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.
[Ответ: 1) a=2g/3; 2) a=g/2.]
4.15.Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m1=100 г и m2=110 г. С каким ускорением а будут двигаться грузы, если масса m блока равна 400 г? Трение при вращении блока ничтожно мало.
[Ответ: a=0,24 м/с2.]
4.16*. Горизонтальный тонкий однородный стержень АВ массы m и длины l может свободно вращаться вокруг вертикальной оси, проходящей через его конец А. В некоторый момент на конец В начала действовать постоянная сила F, которая все время перпендикулярна к первоначальному положению покоившегося стержня и направлена в горизонтальной плоскости. Найти угловую скорость ω стержня как функцию его угла поворота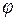 
из начального положения.
[Ответ: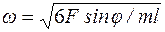 
]
4.17.* Маховик с начальной угловой скоростью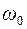 
начинает тормозиться с силами, момент M которых относительно его оси пропорционален квадратному корню из его угловой скорости. Найти среднюю угловую скорость маховика за все время торможения.
[Ответ: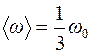 
]
4.18.* Тонкие нити плотно намотаны на концах однородного сплошного цилиндра массы m. Свободные концы нитей прикреплены к потолку кабины лифта. Кабина начала подниматься с ускорением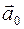 
. Найти ускорение 
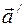цилиндра относительно кабины и силу 
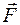, с которой цилиндр действует (через нити) на потолок.
[Ответ: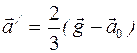 
; 
]
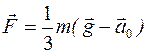4.19.* Однородный цилиндр радиуса R раскрутили вокруг его оси до угловой скорости 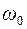и поместили затем в угол (см. рис.4.10). Коэффициент трения между стенками угла и цилиндром равен 
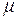. Сколько оборотов сделает цилиндр до остановки?
[Ответ: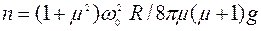 
]
|