Фиктивные переменные в регрессионной модели 5 страница
1. Построить линейную регрессионную модель цены автомобиля, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Если невозможно построить трехфакторную модель, то построить столько моделей с другим числом факторов, сколько необходимо, чтобы охарактеризовать связи между ценой автомобиля и каждым из факторов.
3. Существенно ли влияние пробега, срока эксплуатации и объема двигателя на изменение цены автомобиля?
4. Что сильнее влияет на изменение цены автомобиля — изменение пробега или срока эксплуатации?
5. Спрогнозировать среднюю цену автомобиля с пробегом 150 тыс. км, сроком эксплуатации 10 лет и объемом двигателя 2 л. Если строилось несколько моделей, то прогнозные значения цены рассчитать по всем построенным моделям.
Задача 3.9
По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:
| № банка | Прибыль (млн. руб.) | Собственный капитал (млн. руб.) | Привлеченные средства (млн. руб.) | Депозитная ставка (% годовых) | Кредитная ставка (% годовых) |
| 12,5 | 17,7 | ||||
| 11,7 | 18,2 | ||||
| 11,2 | 19,1 | ||||
| 9,7 | 15,2 | ||||
| 13,5 | 18,5 | ||||
| 10,8 | 18,6 | ||||
| 12,1 | 15,7 | ||||
| 11,7 | 16,6 | ||||
| 13,7 | 17,3 | ||||
| 12,5 | 19,3 | ||||
| 12,8 | 17,8 | ||||
| 11,2 | 14,5 | ||||
| 10,4 | 13,7 |
Требуется:
1. Построить линейную регрессионную модель годовой прибыли банка с полным набором факторов. Оценить параметры модели.
2. Построить линейную регрессионную модель годовой прибыли банка только с существенно влияющими на ее изменение факторами. Оценить параметры модели.
3. Значимо ли статистически уравнение регрессии второй модели?
4. Имеют ли остатки второй регрессии одинаковую дисперсию?
5. Используя вторую модель, сравнить силу влияния факторов на годовую прибыль банка.
Задача 3.10
По четырнадцати страховым компаниям имеются данные, характеризующие зависимость чистой годовой прибыли от годовых размеров собственных средств, страховых резервов, страховых премий и страховых выплат (все в тыс. руб.):
| № компании | Годовая прибыль | Собственные средства | Страховые резервы | Страховые премии | Страховые выплаты |
Требуется:
1. Построить линейную регрессионную модель годовой прибыли страховой компании, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Значимы ли статистически уравнение регрессии и его коэффициенты?
3. Имеют ли остатки регрессии одинаковую дисперсию?
4. Приемлема ли точность регрессионной модели?
5. Дать экономическую интерпретацию коэффициентам уравнения регрессии.
Задача 3.11
По литейному предприятию исследуется влияние объемов производства алюминия, меди и олова на технологические затраты электроэнергии. Имеются данные за одиннадцать месяцев:
| Месяц | Затраты электроэнергии (тыс. кВт×ч) | Объем производства (тонн) | ||
| алюминия | меди | олова | ||
Требуется:
1. Построить линейную регрессионную модель энергозатрат, не содержащую коллинеарных факторов. Оценить параметры модели.
Если невозможно построить трехфакторную модель, то построить столько моделей с другим числом факторов, сколько необходимо, чтобы охарактеризовать связи между энергозатратами и каждым из факторов.
2. Проверить статистическую значимость уравнений регрессии и их отдельных коэффициентов.
3. На сколько в среднем изменяются технологические энергозатраты при увеличении производства каждого из металлов:
а) на одну тонну;
б) на один процент?
4. Выводы по пункту 3 сделать, используя все построенные модели.
Задача 3.12
По литейному предприятию исследуется влияние объемов производства алюминия, меди, олова и магния на технологическое энергопотребление. Имеются данные за тринадцать месяцев:
| Месяц | Затраты электроэнергии (тыс. кВт×ч) | Объем производства (тонн) | |||
| алюминия | меди | олова | магния | ||
Требуется:
1. Построить линейную регрессионную модель энергозатрат с полным набором факторов. Оценить параметры модели.
2. Построить линейную регрессионную модель энергозатрат только с существенно влияющими на их изменение факторами. Оценить параметры модели.
3. Значимо ли статистически уравнение и коэффициенты второй регрессии?
4. Присутствует ли в остатках второй регрессии автокорреляция первого порядка?
5. Какая из двух моделей имеет более высокую точность?
Задача 3.13
Исследуется зависимость цены акции компании «Атон» от цен акций смежных компаний «Бридж», «Вортекс» и «Радон». Имеются данные о результатах биржевых торгов за пятнадцать дней:
| День | Цена акции (руб.) | |||
| «Атон» | «Бридж» | «Вортекс» | «Радон» | |
Требуется:
1. Построить трехфакторную и три однофакторные линейные регрессионные модели цены акции «Атона». Оценить параметры моделей.
2. Проверить статистическую значимость всех уравнений регрессии и их коэффициентов.
3. Используя трехфакторную модель, сравнить силу влияния факторов на изменение цены акции «Атона».
4. Используя трехфакторную и однофакторные модели, спрогнозировать среднюю цену акции «Атона», если предполагается, что цены акций «Бриджа», «Вортекса» и «Радона» составят соответственно 40; 70 и 80 руб. Сравнить результаты расчетов по трехфакторной и однофакторным моделям.
Задача 3.14
По хладокомбинату изучается зависимость месячного объема реализации мороженного от средней цены выпускаемой продукции, затрат на рекламу, среднемесячной температуры воздуха и месячного темпа инфляции. Имеются данные за двенадцать месяцев:
| Месяц | Объем реализации (тыс. руб.) | Цена (руб.) | Затраты на рекламу (тыс. руб.) | Температура воздуха (°С) | Темп инфляции (%) |
| 8,3 | 0,3 | ||||
| 8,3 | 0,4 | ||||
| 8,9 | 0,3 | ||||
| 10,6 | 0,2 | ||||
| 10,7 | 0,7 | ||||
| 10,8 | 0,9 | ||||
| 12,2 | 0,9 | ||||
| 14,2 | 0,4 | ||||
| 14,5 | 0,1 | ||||
| 13,7 | 0,1 | ||||
| 13,3 | 0,5 | ||||
| 12,1 | 0,9 |
Требуется:
1. Построить линейную регрессионную модель объема реализации мороженного, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Значимо ли статистически уравнение регрессии и его коэффициенты?
3. Присутствует ли в остатках регрессии автокорреляция первого порядка?
4. Приемлема ли точность регрессионной модели?
5. Изменение какого из факторов сильнее всего влияет на изменение объема реализации мороженного?
Задача 3.15
По химическому предприятию исследуется зависимость месячной прибыли от объемов производства пластмасс: полиэтилена, полистирола, фторопласта и винипласта. Имеются данные за тринадцать месяцев:
| Месяц | Прибыль (млн. руб.) | Объем производства (тыс. тонн) | |||
| полиэтилена | полистирола | фторопласта | винипласта | ||
Требуется:
1. Построить линейную регрессионную модель прибыли предприятия с полным набором факторов. Оценить параметры модели.
2. Построить линейную регрессионную модель прибыли только с существенно влияющими на ее изменение факторами. Оценить параметры модели.
3. Соответствуют ли остатки регрессии нормальному закону распределения?
4. Приемлема ли точность регрессионной модели?
5. Как в среднем изменяется месячная прибыль при увеличении производства каждой из пластмасс: а) на одну тыс. тонн; б) на один процент?
Задача 3.16
По тринадцати супермаркетам исследуется зависимость квартального торгового оборота от размера торговых площадей, района расположения (центральный или периферийные) и формы собственности (муниципальный или частный). Имеются следующие данные:
| № магазина | Торговый оборот (млн. руб.) | Торговые площади (м2) | Район расположения | Форма собственности |
| периферийный | муниципальный | |||
| периферийный | частный | |||
| центральный | муниципальный | |||
| центральный | муниципальный | |||
| центральный | частный | |||
| периферийный | муниципальный | |||
| центральный | муниципальный | |||
| периферийный | муниципальный | |||
| центральный | частный | |||
| центральный | частный | |||
| центральный | муниципальный | |||
| периферийный | частный | |||
| центральный | частный |
Требуется:
1. Построить линейную регрессионную модель торгового оборота магазина, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Существенна ли разница в торговом обороте магазинов: а) расположенных в центральном и периферийных районах города; б) частных и муниципальных?
3. Соответствуют ли остатки регрессии нормальному закону распределения?
4. Спрогнозировать среднее значение торгового оборота магазина с торговой площадью 4000 м2.
Задача 3.17
По кондитерскому предприятию исследуется зависимость квартального объема реализации выпускаемой продукции от затрат на рекламу и средней заработной платы по региону. Имеются данные за девять кварталов:
| Квартал | Объем реализации (млн. руб.) | Затраты на рекламу (тыс. руб.) | Заработная плата (руб.) |
Требуется:
1. Построить двухфакторную линейную регрессионную модель объема реализации. Оценить параметры модели.
2. Проверить статистическую значимость уравнения регрессии и его коэффициентов.
3. Добавить в регрессионную модель фактор времени и оценить параметры такой модели.
4. Какая из моделей имеет более высокую точность?
5. Дать экономическую интерпретацию коэффициентам обоих уравнений регрессии.
Задача 3.18
Исследуется зависимость биржевой цены акции машиностроительной компании от месячного объема реализованной компанией продукции и индекса фондового рынка. Имеется информация за одиннадцать месяцев (цена акции и индекс рынка даны на конец месяца):
| Месяц | Цена акции (руб.) | Объем реализации (млн. руб.) | Индекс рынка |
Требуется:
1. Построить трехфакторную линейную регрессионную модель цены акции компании, включив в нее в качестве фактора фактор времени. Оценить параметры модели.
2. Проверить статистическую значимость уравнения регрессии и его коэффициентов.
3. Построить линейную модель регрессии только с существенно влияющими на изменение цены акции факторами. Оценить параметры модели.
4. Какая из двух моделей имеет более высокую точность?
5. По более точной модели спрогнозировать цену акции в двенадцатом месяце в предположении, что объем реализованной продукции и индекс рынка будут иметь те же самые значения, что и в одиннадцатом месяце (доверительную вероятность прогноза принять равной 80 %).
Задача 3.19
По девять транспортным предприятиям исследуется зависимость годовой прибыли от количества автомобилей разной грузоподъемности: до 1,5 тонн, свыше 1,5 до 4,5 тонн, свыше 4,5 тонн. Имеются следующие данные:
| № компании | Прибыль (млн. руб.) | Количество автомобилей грузоподъемностью | ||
| до 1,5 т | св. 1,5 до 4,5 т | св. 4,5 т | ||
Требуется:
1. Построить линейную регрессионную модель прибыли транспортного предприятия, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Значимы ли статистически уравнение и коэффициенты регрессии?
3. Соответствуют ли остатки регрессии нормальному закону распределения?
4. Сколько дополнительной прибыли приносит в среднем автомобиль каждого вида?
5. Изменение числа автомобилей какого вида наиболее сильно влияет на изменение прибыли?
Задача 3.20
По торговой фирме исследуется влияние стажа работы, уровня образования и пола менеджера по продаже на размер дохода от реализации товаров, принесенного фирме за год. Имеются сведения по десяти менеджерам:
| Менеджер | Доход (млн. руб.) | Стаж (лет) | Образование | Пол |
| 1. Иванова | высшее | женский | ||
| 2. Петров | среднее | мужской | ||
| 3. Кузнецов | высшее | мужской | ||
| 4. Светлова | среднее | женский | ||
| 5. Сидоренко | высшее | женский | ||
| 6. Калинин | высшее | мужской | ||
| 7. Крымова | высшее | женский | ||
| 8. Жуков | высшее | мужской | ||
| 9. Баранова | среднее | женский | ||
| 10. Семенов | высшее | мужской |
Требуется
1. Построить линейную регрессионную модель дохода с полным набором факторов. Оценить параметры модели.
2. Значимо ли статистически уравнение регрессии?
3. Существенна ли разница в размере дохода, принесенного:
а) менеджерами с высшим и средним образованием?
б) мужчинами и женщинами?
4. Построить линейную регрессионную модель только со статистически значимыми факторами. Оценить параметры модели.
5. Дать экономическую интерпретацию коэффициентам уравнения регрессии последней модели.
Тестовые вопросы для самоконтроля
Предлагаемые тесты посвящены вопросам построения модели множественной регрессии и проверки выполнения предпосылок метода наибольших квадратов. Из перечня приведенных ответов только один является правильным (см. с. 151).
Вопрос 3.1
Исследуется зависимость официального курса доллара США (Y, руб. за доллар) от официальных курсов евро (X1, руб. за евро), японской иены (X2, руб. за 100 иен) и английского фунта стерлингов (X3, руб. за фунт). Имеются данные о курсах валют, установленных Центральным банком Российской Федерации за десять последовательных дней:
| День | Y | X1 | X2 | X3 |
| 28,1237 | 36,1305 | 26,9746 | 52,6391 | |
| 28,1872 | 35,9781 | 26,8016 | 52,3267 | |
| 28,1330 | 35,9737 | 26,6765 | 52,2627 | |
| 28,0853 | 36,0025 | 26,5934 | 52,2808 | |
| 28,0688 | 36,1302 | 26,5376 | 52,4381 | |
| 28,0306 | 36,2856 | 26,7009 | 52,5854 | |
| 28,0207 | 36,3428 | 26,6788 | 52,9031 | |
| 28,0016 | 36,4749 | 26,6352 | 52,9930 | |
| 27,9998 | 36,5453 | 26,6006 | 52,8160 | |
| 27,9359 | 36,5066 | 26,5097 | 52,8994 |
Матрица парных коэффициентов корреляции переменных имеет вид:
| Y | X1 | X2 | X3 | |
| Y | ||||
| X1 | -0,903 | |||
| X2 | 0,633 | -0,389 | ||
| X3 | -0,798 | 0,925 | -0,161 |
Какие факторы целесообразно включить в линейную модель регрессии?
Ответ:
а) Все факторы.
б) ФакторыX1 и X2.
в) ФакторыX1 и X3.
г) Только фактор X1.
д) Только фактор X2.
е) Только фактор X3.
Вопрос 3.2
По кондитерскому предприятию имеются данные за двенадцать месяцев, характеризующие зависимость месячного объема реализованной продукции (переменная Y, тыс. руб.) от затрат в предыдущем месяце на теле- и радиорекламу (факторы X1 и X2 соответственно, тыс. руб.):
| Месяц | Y | X1 | X2 |
| январь | |||
| февраль | |||
| март | |||
| апрель | |||
| май | |||
| июнь | |||
| июль | |||
| август | |||
| сентябрь | |||
| октябрь | |||
| ноябрь | |||
| декабрь |
Было получено уравнение линейной регрессии
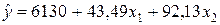 .
.
Суммы квадратов отклонений зависимой переменной Y от своего среднего значения составляют:
