Выявление и исключение грубых погрешностей (промахов)

Грубые погрешности измерений (промахи) могут сильно исказить 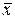, 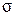и доверительный интервал, поэтому их исключение из серии измерений обязательно. Обычно они сразу видны в ряду полученных результатов, но в каждом конкретном случае это необходимо доказать. Существует ряд критериев для оценки промахов.

Критерий 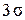. В этом случае считается, что результат, возникающий с вероятностью 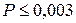, малореален и его можно квалифицировать промахом, т.е. сомнительный результат 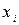отбрасывается, если

.

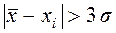Величины 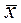и 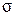вычисляют без учета 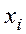. Данный критерий надежен при числе измерений .

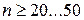Если 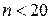, целесообразно применять критерий Романовского.

При этом вычисляют отношение 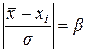и полученное значение 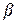сравнивают с теоретическим 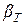- при выбираемом уровне значимости Р по табл. 2.

Таблица 2

Уровень значимости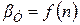

Вероятность, Р	Число измерений
n=4	n=6	n=8	n=10	n=12	n=15	n=20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Обычно выбирают 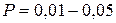, и если 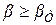, результат отбрасывают.

Если число измерений невелико (до 10), то можно использовать критерий Шовенэ. В этом случае промахом считается результат 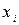, если разность 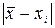превышает значение 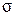, приведенные ниже в зависимости от числа измерений:

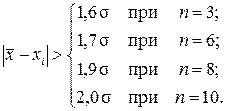
Критерий Шарлье используется, если число наблюдений в ряду велико (n >20). Тогда по теореме Бернулли число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину К_шS_x, будет n [1-Ф(Ф(К_ш))], где Ф(К_ш) – значение нормированной функции Лапласа для

Х= К_ш

Если сомнительным в ряду результатов наблюдений является один результатов, то n·[1-Ф(К_ш)] =1. Отсюда Ф(К_ш)= (n-1)/n. Значение критерия Шарлье приведены в табл. 3.

Пользуясь критерием Шарлье, отбрасывают результат, для значения которого в ряду из n наблюдений выполняется неравенство │x_i- 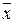│>К_шS_x.

Таблица 3

Значения критерия Шарлье

n
Кш	1,3	1,65	1,96,	2,13	2,24	2,32	2,58

Вариационный критерий Диксона – удобный и достаточно мощный (с малыми вероятностями ошибок). При его применений полученные результаты наблюдений записывают в вариационный возрастающий ряд x₁, x_2, … , x_n (x₁<x₂<...<x_n). Критерии Диксона определяется как К_д = (x_n-x_n-1)/(x_n-x₁).

Критическая область для этого критерия P(К_д>Z_q) = q. Значения Z_q. Значения Z_q. приведены в табл. 4.

Таблица 4

Значения критерия Диксона

n	Zq при q, равном
0,10	0,05	0,02	0,01
	0,68	0,76	0,85	0,89
	0,48	0,56	0,64	0,70
	0,40	0,47	0,54	0,59
	0,35	0,41	0,48	0,53