Радиально-сферическое движение несжимаемой

Жидкости по закону Дарси

Фильтрационный поток называется радиально-сферическим, «если векторы скорости фильтрации направлены в пространстве по прямым, радиально сходящимся к од­ной точке (или расходящимся от нее).

Благодаря центральной симметрии дав­ление и скорость фильтрации зависят и в этом случае только от одной координаты r, отсчитываемой от центра (рис. 8). При­мером потока, весьма близкого радиально-сферическому, является приток жидко­сти к гидродинамически несовершенной скважине малого диаметра, едва вскрыв­шей непроницаемую горизонтальную 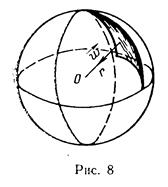кров­лю однородного пласта большой мощности (теоретически бесконечной). Если на забое скважины, представленной в виде полусферы радиуса r_с, поддерживается постоянное приведенное давление, 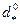, а на достаточно большом расстоянии от скважины, на полусферической поверхности радиуса R_к сохраняется посто­янное давление 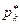и фильтрация в однородном пласте проис­ходит по закону Дарси, то объемный дебит скважины опреде­ляется по формуле

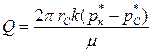(III.17)

Приведенное давление в любой точке пласта определяется по формуле

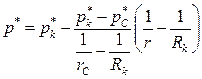(III.18)

азакон движения частиц вдоль линии тока от точки с координатой r₀ до точки с координатой r описывается уравнением

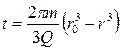(III.19)

Задача 20

Определить дебит дренажной галереи шириной B = 100 м, если мощность пласта h=10 м, расстояние до контура питания l = 10 км, коэффициент проницаемости пласта k=1 Д, динамический коэффициент вязкости жидкости μ = l сП, давление на контуре питания p_к = 9,8 МПа (100 кгс/см²) и давление в галерее p_г = 7,35 МПа (75 кгс/см²). Движение жидкости напорное, подчиняется закону Дарси.

Ответ: Q = 21,6 м³/сут.

Задача 21

Определить коэффициент проницаемости пласта (в различ­ных системах единиц), если известно, что в пласте происходит одномерное, прямолинейно-параллельное установившееся движение однородной жидкости по закону Дарси. Гидравлический уклон i = 0,03, ширина галереи В = 500 м, мощность пласта h=6 м, плотность жидкости ρ = 850 кг/м³, динамический коэф­фициент вязкости μ = 5 сП и дебит галереи Q = 30 м³/сут.

Ответ: k=2,27 Д=32∙10^-8 см²=2,32∙10^{-12 м2}.

Задача 22

Показать графически распределение давления и найти градиент давления при прямолинейно-параллельном движении в пласте несжимаемой жидкости по линейному закону фильтрации, используя следующие данные: длина пласта l_к = 5 км, мощность пласта h=10 м, ширина галереи B = 300 м, коэффи­циент проницаемости пласта k = 0,8 Д, давление в галерее р_г = 2,94 МПа (30 кгс/см²), динамический коэффициент вязкости жидкости μ = 4 сП, дебит галереи Q = 30 м³/сут.

Ответ: p = 5,78 - 0,0568∙10^-2х (х в м, р в МПа), - dp/dx = 0,0568∙10^-2 МПа/м.

Задача 23

Определить дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания р_к =9,8 МПа (100 кгс/см²), давление на забое скважины р_с =7,35 МПа (75 кгс/см²), коэффициент проницаемости пласта k = 0,5 Д, мощность пласта h = 15 м, диаметр скважины Dc=24,8 см, радиус контура питания R_к=10 км, динамический коэффициент вязкости жидкости μ = 6 мПа∙с и плотность жидкости р = 850 кг/м³.

Ответ: Q_m= 127 т/сут.

Задача 24

Определить давление на расстоянии 10 и 100 м от оси скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, счи­тая, что коэффициент проницаемости пласта k = 0,5 Д, мощ­ность пласта h = 10 м, давление на забое скважины р_с = = 7,84 МПа (80 кгс/см²), радиус скважины r_с== 12,4см, дина­мический коэффициент вязкости нефти μ = 4∙10^-3 кг/м∙с, плотность нефти ρ = 870 кг/м³ и массовый дебит скважины Q_m = 200 т/сут.

Ответ: p₁=9,28 МПа; p₂ = 10,06 МПа.

Задача 25

Построить индикаторную линию (зависимость дебита Q от перепада давления Δр = р_к —р_с), имеющуюся при установив­шейся плоскорадиальной фильтрации жидкости по линейному закону, если известно, что давление на контуре питания p_к = 8,82 МПа (90 кгс/см²), коэффициент проницаемости пласта k = 600 мД, мощность пласта h=10 м, диаметр скважины D_c = = 24,8 см, расстояние от оси скважины до контура питания R_k=10 км и динамический коэффициент вязкости нефти μ = 5 мПа∙с.

Ответ: индикаторная линия — прямая, описываемая уравне­нием Q = 5,77 Δр (Q в м³/сут, Δр в кгс/см²).

Задача 26

Определить коэффициент гидропроводности пласта kh/μ по данным о коэффициенте продуктивности скважины. Извест­но, что фильтрация происходит по закону Дарси, коэффициент продуктивности K=18 т/сут (кгс/см²), среднее расстояние меж­ду скважинами 2σ = 1400 м, плотность ρ=925 кг/м³, радиус скважины r_с= 0,1 м.

Ответ:kh/μ = 3,18∙10^-9 м⁴∙с/кг (318 Д∙см/сП).

Задача 27

Определить средневзвешенное по объему пластовое давле­ние, если известно, что давление на контуре питания р_к = 9,8 МПа (100 кгс/см²), давление на забое возмущающей скважины p_с = 7,84 МПа (80 кгс/см²), расстояние до контура питания R_к = 25 км, радиус скважины r_с = 10 см. В пласте име­ет место установившееся плоскорадиальное движение несжи­маемой жидкости по закону Дарси.

Ответ: р = 9,72 МПа (99,19 кгс/см²).

Задача 28

Определить относительное понижение s_p/s= (H_к—Н)/(Н_к—H_с) пьезометрического уровня в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях 1 м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси. Радиус скважины r_с = 0,1 м, расстояние до контура питания R_к=100 км.

Ответ: s_p/s равно соответственно 0,83; 0,50; 0,33; 0,167.

Задача 29

Определить время отбора нефти из призабойной зоны скважины радиусом r₀=100 м, если мощность пласта h=10 м, коэффициент пористости пласта m = 20%, массовый дебит нефти Q_m =40 т/сут, плотность ее ρ= 920 кг/м³, r_с = 0,1 м.

Ответ: Т = 1440 сут.

Задача 30

Определить время t, за которое частица жидкости подойдет к стенке скважины с расстояния r₀ = 200 м, если коэффициент проницаемости пласта k=1 Д, динамический коэффициент вяз­кости нефти μ = 5 сП, депрессия во всем пласте радиусом R_к = 1 км составляет р_к—р_с= 10 кгс/см²; мощность пласта h=10м, коэффициент пористости пласта m = 15%, радиус скважины r_c = 10 см.

Ответ: t = 1600 сут.

Задача 31

Как изменится дебит скважины Q при увеличении радиуса скважины вдвое?

1. Движение происходит по линейному закону фильтрации.

2. Фильтрация происходит по закону Краснопольского.

Начальный радиус скважины r_с = 0,1 м. Расстояние до контуpa питания R_к = 5 км.

Ответ: 1) Q’: Q=l,07; 2) Q’: Q= 1,41, т. е. при движении жидкости по линейному закону фильтрации влияние изменения радиуса скважины менее интенсивно, чем при движении по закону Краснопольского.

Задача 32

Найти изменение перепада давления Δр при увеличении радиуса скважины вдвое, при котором дебит остается прежним. Рассмотреть два случая, как в предыдущей задаче. Начальный радиус скважины r_с = 0,1 м, расстояние до контура питания R_к= 1 км.

Ответ: 1) Δр'/Δр = 0,925, 2) Δр'/Δр = 0,5.

Задача 33

Во сколько раз необходимо увеличить радиус скважины, чтобы дебит ее при прочих равных условиях удвоился?

1) Движение жидкости происходит по закону Дарси.

2) Жидкость фильтруется по закону Краснопольского. На­чальный радиус скважины r_с = 0,1 м. Расстояние до контура питания R_к= 1 км.

Ответ: 1) n=100, r'_c=10 м; 2) n = 4, r'_с = 0,4 м.

Задача 34

Скважина радиусом r_с=10 см расположена в центре круго­вого пласта радиусом R_к = 350 м. Коэффициент проницаемости пласта k = 0,8 Д, мощность h=12м, динамический коэффициент вязко­сти нефти μ=5 сП. Определить дебит скважины, считая, что за­лежь по контуру радиуса R_к ча­стично непроницаема (рис. 9). Кон­тур питания представляет собой в плане дугу окружности радиусом R_к с центральным углом α = 120°. Давление на контуре питания р_к = 27,9 МПа (285 кгс/см²), давление на забое скважины р_с = 7,84 МПа (80 кгс/см²).

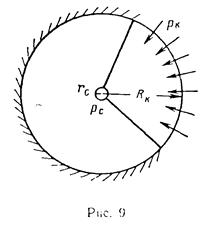Решение. Задачу можно свести к плоскорадиальной, если в форму­ле Дюпюи за контурное давление принять средневзвешенное по длине окружности давление р_к

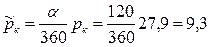МПа,

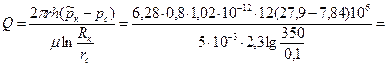
= 2,22-10~³ м³/с - 192 м³/сут.

Задача 35

Сколько жидкости следует закачивать в пласт в единицу времени через нагнетательную скважину, если необходимо, чтобы давление в скважине поддерживалось в процессе за­качки на Δр=1,47 МПа (15 кгс/см²) выше давления, устано­вившегося в пласте на расстоянии r = 2 км от скважины? Имеет место закон Дарси. Динамический коэффициент вязко­сти μ =1 сП, коэффициент проницаемости пласта k = l50 мД, мощность пласта h =10 м, радиус скважины r_с = 10 см.

Ответ: Q=123 м³/сут.

Задача 36

Определить приведенное давление в точках, отстоящих на r = 20 м, 10 м, 5 м, 1,5 м, 1 м от центра забоя скважины, вскрывшей пласт бесконечной мощности на величину b = 0,5 м. На расстоянии R_к=1000м приведенное давление р_к*= 9,8 МПа (100 кгс/см²), на забое скважины р_с*=7,35 МПа (75кгс/см²), рллиус скважины r'_c = 12,4см. Фильтрация к скважине происходит по закону Дарси.

Указание.Представляя забой скважины в виде полусферы, Равновеликой по площади забою действительной скважины, определить радиус полусферы r_c(2πr'_сb=2πr²_c).

Ответ: соответственно р* = 9,77; 9,74; 9,68; 9,39; 9,19 МПа.

Задача 37

Скважина вскрывает пласт бесконечно большой мощности на небольшую глубину. Считая движение радиальносферическим, определить время перемещения частиц жидкости вдоль линий тока от точки с координатой r₀=100 м до точки с коор­динатой r = 5 м. Скважина эксплуатируется с постоянным дебитом Q = 120м³/сут, коэффициент пористости пласта m = 15%.

Ответ: t = 7,15 лет.