Аксиоматическое определение вероятности

Напомним, что классическое определение вероятности относится к пространствам элементарных исходов 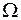, состоящим из конечного числа равновозможных элементов, статистическое — к счетным. Геометрическое определение – к пространствам , представляющим собой области, имеющие в зависимости от длину, площадь, объём или обобщённый объём, т.е. являющиеся измеримыми. В качестве событий в геометрической схеме рассматриваются также измеримые подмножества из .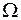

Мы определили событие как произвольное подмножество пространства 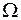, это определение допустимо и не приводит к противоречиям только в том случае, когда множество 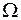является конечным или счетным. В случае несчетного множества 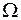уже нельзя построить логически непротиворечивую теорию, если называть событием любое подмножество .

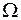Противоречия, возникающие при этом, довольно длительное время сдерживали развитие теории вероятностей как раздел математики. Только в 30-х годах XX века академиком А.Н. Колмогоровым было предложено аксиоматическое построение теории вероятностей, которое освободило теорию от противоречий и связало ее с основными разделами математики.

Аксиоматическое определение, сохраняя основные свойства вероятности, подмеченные в рамках классической и геометрической схем, позволяет ввести это понятие для пространств элементарных исходов произвольной природы.

Основные новшества, которые внес Колмогоров, касались определения события. Теперь событием называют уже не любые подмножества из 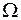, которые принадлежат некоторому классу подмножеств S.

Алгебра событий. Пусть Ω – пространство элементарных исходов некоторого случайного эксперимента (т. е. непустое множество произвольной природы). Мы собираемся определить набор подмножеств Ω, которые будут называться событиями, и затем задать вероятность как функцию, определённую только на множестве событий.

Итак, событиями мы будем называть не любые подмножества Ω, а лишь элементы некоторого выделенного набора подмножеств Ω. При этом необходимо позаботиться, чтобы этот набор подмножеств был замкнут относительно обычных операций над событиями, т. е. чтобы объединение, пересечение, дополнение событий снова давало событие. Сначала введём понятие алгебры событий.

Определение 6.1. Множество A, элементами которого являются подмножества множества Ω (не обязательно все) называется алгеброй (алгеброй событий), если оно удовлетворяет следующим условиям:

(A1) Ω ∈ A (алгебра событий содержит достоверное событие);

(A2) если A, то A (вместе с любым событием алгебра

содержит противоположное событие);

(A3) если A и A, то A (вместе с любыми двумя событиями алгебра содержит их объединение).

Из (A1) и (A2) следует, что пустое множество Æ также содержится в A.

Пример 6.1. Пусть Ω = {♠, ♣, ♦, ♥} — пространство элементарных исходов. Следующие наборы подмножеств Ω являются алгебрами:

1. A = {Ω, Æ} = {{♠, ♣, ♦, ♥}, Æ} — тривиальная алгебра.

2. A = {Ω, Æ, {♥}, Ω \ {♥}} = {{♠, ♣, ♦, ♥}, Æ, {♥}, {♠, ♣, ♦}}.

3. A = {Ω, Æ, A, A} = {{♠, ♣, ♦, ♥}, Æ, 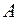, 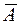}, где 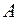– произвольное подмножество Ω (в предыдущем примере A = {♥}).

В теории вероятностей зачастую необходимо объединять счетные наборы событий и считать событием результат такого объединения. При этом свойства (А3) оказывается недостаточно – из него не вытекает, что объединение счетной последовательности множеств из алгебры снова принадлежит алгебре.

Определение 6.2. Множество S, элементами которого являются подмножества множества Ω (не обязательно все) называется

σ – алгеброй, если выполнены следующие условия:

(S1) Ω∈S (σ-алгебра событий содержит достоверное событие);

(S2) если 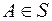, то (вместе с любым событием σ-алгебра содержит противоположное событие);

(S3) если , то (вместе с любым счетным набором событий σ-алгебра содержит их объединение).

Если пространство элементарных исходов – конечно, то σ-алгеброй событий будет множество всех его подмножеств, включая пустое множество.

Всякая σ-алгебра является алгеброй, но не наоборот.

Пример 6.2. Пусть Ω = R, и пусть A — множество, содержащее любые конечные подмножества R (т. е. состоящие из конечного числа точек, в том числе пустое) и их дополнения. В частности, множество {0, 1, е} принадлежит A, множество (−∞, −3,3)∪ ∪(−3,3, 7) ∪ (7, ∞) принадлежит A.

Легко проверить, что множество A является алгеброй. Действительно, пустое множество и само Ω = R там содержатся, дополнение к любому конечному подмножеству множества вещественных чисел содержится в A по определению, дополнение к множеству вида R \ А для конечных А совпадает с А и также принадлежит A по определению. Свойство (A3) проверяется непосредственно: объединение любых конечных множеств снова конечно и поэтому принадлежит A. Объединение конечного множества с множеством вида R \А, где А конечно, есть снова множество вида R \ B, где B конечно (или пусто). Объединение двух множеств R \ A и R \ B, являющихся дополнениями до R конечных множеств A и B, есть снова множество такого же вида.

Однако алгебра A не содержит ни одного счётного множества точек. Действительно, объединяя конечные множества в конечном числе, мы можем получить только конечное множество. Например, натуральный ряд N не принадлежит A. Поэтому A не является σ-алгеброй: для бесконечной, но счётной последовательности одноточечных множеств из A их объединение N = не принадлежит A.

Все алгебры из примера 6.1 являются σ-алгебрами, поскольку содержат лишь конечное число элементов. Вообще, на конечном множестве Ω понятия алгебры и σ-алгебры совпадают.

Определение 6.3. Пусть Ω — пространство элементарных исходов, S — σ-алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на (Ω, S) называется функция P: S → R, удовлетворяющая следующим аксиомам:

А1. Аксиома неотрицательности: вероятность любого события 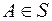неотрицательна, т. е. .

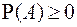А2. Аксиома нормированности: вероятность достоверного события равна единице, т. е. .

A3. Аксиома аддитивности: для любого счётного набора попарно несовместных событий имеет место равенство

.

Определение 6.4. Совокупность объектов (Ω, S, P ), где Ω — пространство элементарных событий, S — σ-алгебра событий, P — числовая функция, удовлетворяющая аксиомам A1-A3, называется вероятностным пространством случайного эксперимента.

Вероятностное пространство служит математической моделью любого случайного явления.

Свойства вероятностей

Приведем ряд свойств вероятности, являющихся следствием аксиом Колмогорова.

С 1. P(Æ) = 0.

Доказательство.

Пусть события Æ, где , попарно несовместны, и их объединение есть также пустое множество. По аксиоме A3,

(Æ) (Æ)

Это возможно только в случае P(Æ) = 0.

Заметим, что из не следует, что Æ.

С 2. Для любого конечного набора попарно несовместных событий A1 имеет место равенство

.

Доказательство

Положим Æ при любом . По свойству С 1 вероятности этих событий равны нулю. События ,Æ, Æ,... попарно несовместны, и по аксиоме (А3)

.

Из последнего свойства можно получить сразу несколько свойств.

С 3. Для любого события : .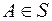

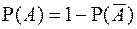С 4. Если A⊆B, то .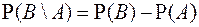

С 5. (свойство монотонности вероятности). Если A⊆B, то .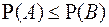

С 6. Для любого события A выполнено: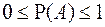

С 7. Всегда P(A∪B)=P(A)+P(B)−P(A∩B).

С 8. Всегда выполняется P(A∪B)≤ P(A)+ P(B).

С 9. Всегда выполняется .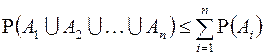

С 10. Для любого конечного набора событий имеет место равенство:

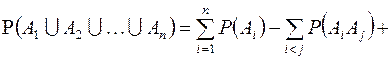(6.1)

.

Последнее свойство называют формулой включения и исключения. Она удобна в случае, когда для вычисления вероятности некоторого события A нельзя разбить это событие на удобные попарно несовместные события, но удаётся разбить событие A на простые составляющие, которые, однако, совместны.

Пример 6.3. Из колоды, содержащей 36 карт, наудачу вынимают три карты. Найти вероятность того, что среди них окажется хотя бы один валет.

Решение. Пусть 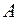={среди вынутых карт окажется хотя бы один валет}, 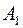={появление одного валета}, 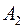={двух валетов}, ={трех валетов}. Тогда , причем события несовместные. Поэтому, согласно свойству С2, . Число всевозможных случаев выбора трех карт из 36 равно

;

число случаев, благоприятных событиям , соответственно равно

,

,

.

Таким образом,

Заметим, что задача решается проще, если воспользоваться свойством С3. Находим , где 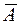={среди вынутых карт нет ни одного валета}.

;

Тогда

Ответ: .

Пример 6.4. («задача о рассеянной секретарше».) Есть писем и подписанных конвертов. Письма раскладываются в конверты наудачу по одному. Найти вероятность того, что хотя бы одно письмо попадет в предназначенный ему конверт.

Решение. Данная задача легче всего решается с помощью свойства С 10.

Пусть событие 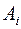, , ={ 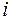-е письмо попало в свой конверт}. Тогда = {хотя бы одно письмо попало в свой конверт}.

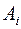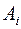Так как события совместны, будем использовать формулу (6.1). Вычислим вероятности всех событий и их пересечений по классическому определению вероятности. Элементарными исходами будут всевозможные перестановки (размещения) писем по конвертам. Их общее число есть , и событию благоприятны из них, а именно любые перестановки всех писем, кроме 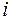-го, лежащего в своём конверте.

Поэтому

для всех .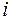

Аналогично для имеем

.

Вероятность для трех событий равна

.

Аналогично посчитаем вероятности пересечений любого другого числа событий.

.

Вычислим количество слагаемых в каждой сумме в формуле (6.1). Например, в сумме по ровно слагаемых — ровно столько двухэлементных множеств можно образовать из элементов, и каждое такое множество встречается в индексах данной суммы единожды.

Подставляя все вероятности в формулу (6.1), получим:

Заметим, что при .

Действительно,

,

откуда

.

Тогда

.

РЕШЕНИЕ ЗАДАЧ

Задача 1. Образуют ли полную группу следующие группы событий:

a) Опыт – бросание монеты. События:

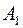= {появление герба};

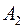= {появление решки}.

b) Опыт – бросание двух монет. События:

= {появление двух гербов};

= {появление двух решек}.

c) Опыт – два выстрела по мишени. События:

= {хотя бы одно попадание};

= {хотя бы один промах}.

d) Опыт – вынимание карты из колоды. События:

= {появление карты червонной масти};

= {появление карты трефовой масти}.

= {появление карты бубновой масти}?

Ответ: a) да, b) нет, c) да, d) нет.

Задача 2. Являются ли несовместными следующие события:

a) Опыт – бросание монеты. События:

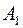= {появление герба};

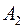= {появление решки}.

b) Опыт – бросание двух монет. События:

= {появление герба на первой монете};

= {появление решки на второй монете}.

c) Опыт – два выстрела по мишени. События:

= {ни одного попадания};

= {одно попадание};

= {два попадания}.

d) Опыт – вынимание двух карт из колоды. События:

= {появление двух черных карт};

= {появление туза};

= {появление короля}?

Ответ: a) да, b) нет, c) нет, d) нет.

Задача 3. Являются ли равновозможными следующие события:

a) Опыт – бросание симметричной игральной кости. События:

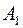= {выпадение шести очков};

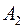= {выпадение двух очков}.

b) Опыт – бросание неправильной (погнутой) монет. События:

= {появление герба};

= {появление решки}.

c) Опыт – бросание двух монет. События:

= {появление двух гербов};

= {появление двух решек};

= {появление одного герба и одной решки};

d) Опыт – бросание симметричной игральной кости. События:

= {появление не менее трех очков};

= {появление не более четырех очков}?

Ответ: a) да, b) нет, c) нет, d) да.

Задача 4. Являются ли случаями следующие группы событий:

a) Опыт – бросание монеты. События:

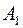= {появление герба};

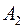= {появление решки}.

b) Опыт – бросание игральной кости. События:

= {появление не более двух очков};

= {появление трех или четырех очков};

= {появление не менее пяти очков}.

c) Опыт – бросание двух монет. События:

= {появление двух гербов};

= {появление двух решек};

= {появление одного герба и одной решки};

d) Опыт – вынимание двух карт из колоды. События:

= {появление двух красных карт};

= {появление двух черных карт}?

Ответ: a) да, b) да, c) нет, d) нет.

Задача 5.Показать, что для любых событий :

(формула Моргана).

Решение: Пусть , тогда , w .

Формула следует из определения равносильности событий.

Задача 6.Изобразить на диаграмме Эйлера – Венна следующие события:

а) ; б) ; в) ; г) .

Ответ:

а) ;

Рис. 7.1

б) ;

Рис. 7.2

в) ;

Рис. 7.3

г) .

Рис. 7.4

Задача 7.Производится опыт – подбрасывание игрального кубика. Элементарные события: = {выпадение к очков ( к = )}. Построены события:

А = {выпадение чётного числа очков};

В = {выпадение нечётного числа очков};

С = {выпадение числа очков, кратного 4};

D = {выпадение числа очков, больше 3}.

Выразить события А, В, С, D через .

Решение:

1) Событие А наступит тогда и только тогда, когда выпадет либо два, либо четыре, либо шесть очков, то есть А₂, или А₄, или А₆, следовательно, событие А можем представить следующим образом:

.

2) Событие В наступит тогда и только тогда, когда выпадет либо одно, либо три, либо пять очков, то есть А₁, или А₃, или А₅, тогда

.

3) Событие С наступит тогда и только тогда, когда выпадет только 4 очка, т.е.,

.

4) Числа 4, 5 и 6 больше трех, следовательно

Задача 8.Пусть 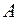, , 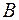– произвольные события. Что означают следующие события:

1) ;

2) ;

3)

4) ;

5) ;

6) ?

Решение:

1) В соответствии с определением 1.8, – произведение трёх событий 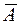, , 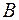, которые происходят одновременно, причём 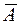– событие, противоположное событию А. Следовательно, означает, что событие А не произошло, а событие В и С произошли.

Рассуждая аналогичным образом, заключаем, что:

2) = {ни одно из трёх данных событий не произошло};

3) = {не произошли одновременно все три события};

4) = {хотя бы одно из трёх событий не произошло};

5) = {произошло ровно одно из трёх событий};

6) = {произошло не более одного (менее одного) из трёх событий}.

Задача 9. Цепь состоит из системы контактов, изображенной на схеме 7.1. Событие {контакт замкнут}.

Схема 7.1.

Записать следующие события:

1) цепь замкнута;

2) цепь разомкнута.

Решение:

1) Цепь будет замкнута в том случае, когда работает хотя бы один контакт при параллельном соединении и оба контакта при последовательном, т.е.

.

2) Цепь разомкнется в том случае, когда разомкнуты все контакты при параллельном соединении или разомкнут один из контактов в последовательном соединении, т.е.

.

Ответ:1) ; 2) .

Задача 10. На множестве натуральных чисел задана функция: каждому ставится в соответствие число следующим образом: , , , . Остальные . Проверить, является ли эта функция вероятностью выбора одного натурального числа? Найти вероятность следующих событий:

a) ;

b) ;

c)

d) .

Решение.

Проверим, является ли заданная функция вероятностью. Для этого проверим выполнение определения 2.3:

Выполняется.

a) .

b) .

c)

d)

Ответ: a) 0,4; b) 0; c) 0,6; d) 0,3.

Задача 11.На множестве задана функция , Проверить, равна ли сумма вероятностей элементарных исходов единице?

Решение:

.

Заметив, что ряд представляет собой разложение , получаем

. ч.т.д.

Ответ:равна.

Задача 12.На множестве задана функция , Проверить, равна ли единице сумма вероятностей элементарных исходов? Найти вероятность события .

Решение:

.

Множитель представляет собой сумму бесконечно убывающей геометрической прогрессии с , следовательно,

.

.

Ответ: .

Задача 13. Подбрасываются две монеты. Какова вероятность появления герба хотя бы на одной из них?

Решение: Обозначим Г – выпадение герба, Р – выпадение решки. Построим пространство элементарных событий .

Выпадению герба благоприятствуют элементарные исходы . Тогда, согласно формуле (3.1)

Ответ: .

Задача 14.Трижды подбрасывается игральная кость. Найти вероятность получить в сумме четыре очка.

Решение. Общее число равновозможных элементарных исходов . Сумма очков равна четырем, если на два раза выпали единицы и один раз – двойка. Этому событию благоприятствуют три элементарных исхода: . По формуле (1.3) искомая вероятность равна

.

Ответ: .

Задача 15.Из букв слова «дифференциал» наугад выбирается одна буква. Какова вероятность того, что эта буква будет:

a) гласной;

b) согласной;

c) буквой «ы»?

Решение:В слове «дифференциал» 12 букв, из них 5 гласных и 7 согласных.

а) Пусть событие А = {гласная буква}, тогда число благоприятствующих элементарных исходов m = 5, число всевозможных исходов n = 12, согласно формуле (3.1)

;

б) Пусть событие В = {согласная буква}. В этом случае m = 7, n = 12, тогда

;

в) Пусть событие С = {буква «ы»}. Т.к. в слове «дифференциал» такой буквы нет, т.е. m = 0, получаем

.

Ответ: а) 0,417 б) 0,583 в) 0.

Задача 16.В книге 300 страниц. Чему равна вероятность того, что наугад открытая страница будет иметь порядковый номер, кратный 5?

Решение:По условию задачи число всех равновозможных элементарных исходов, образующих полную группу событий, будет . Номер, кратный 5 имеет вид 5k, где k – натуральное число, причем , откуда . Следовательно,

.

Ответ: .

Задача 17.Подбрасываются два игральных кубика. Подсчитывается сумма очков на верхних гранях. Что вероятнее – получить в сумме 7 или 8?

Решение:Пусть А = {выпало 7 очков}, В= {выпало 8 очков}. Событию А благоприятствуют 6 элементарных исходов: (1;6), (2;5), (3;4), (5;2), (6;1), а событию В – 5 исходов: (2;6), (3;5), (4;4), (5;3), (6;2). Всех равновозможных элементарных исходов

.

По формуле (3.1)

;

.

Видим, что .

Ответ: Получить в сумме 7 очков вероятнее, чем 8.

Задача 18.В урне содержатся 3 красных и 7 белых шаров. Наугад извлекаются 2 шара. Найти вероятность того, что

а) оба шара окажутся красными (событие );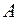

б) один красный, другой белый (событие );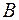

в) оба шара окажутся белыми (событие );

Решение:Всего 10 шаров, из них мы выбираем два шара, поэтомудля всех трёх случаев число всевозможных исходов

.

а) В первом случае мы выбираем 2 красных шара из трёх, поэтому

,

тогда по формуле (3.1)

;

б) Теперь один шар красный, другой белый, причём красный выбираем из трёх , а белый из семи, т.е.

,

согласно формуле (3.1)

;

в) Выбираем два белых шара. Рассуждая аналогично, получаем

,

.

Ответ: а) ; б) ; в) .

Задача 19.Из одного байта, в котором сдержатся три нуля, извлекаются три бита. Какова вероятность, что их конъюнкция будет логической единицей?

Решение. В одном байте содержится 8 бит. Поэтому общее число способов извлечь три бита равно

Конъюнкция будет логической единицей в том случае, если все три бита являются единицами. Это можно осуществить 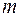способами:

Тогда искомая вероятность

.

Ответ: .

Задача 20.В ящике находится 15 красных, 9 синих и 6 зелёных шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что вынуты 1 зелёный, 2 синих и 3 красных шара?

Решение:Пусть событие А = {вынуты 1 зелёный, 2 синих и 3 красных шара}. В ящике 30 шаров. Вынуты 6 шаров, поэтому число всех равновозможных элементарных исходов будет

.

Найдём число исходов, благоприятствующих появлению событию А. Три красных шара выбираем из 15, 2 синих – из 9, а 1 зелёный – из 6. По правилу произведения

,

тогда по формуле (3.1)

.

Ответ: 0,17.

Задача 21. Петр на рынке купил кассету из 10 яиц. Но он не знал, что 2 из них испорчены. На завтрак Петр ест яичницу из трех яиц. Какова вероятность, что Петр будет готовить яичницу дважды?

Решение. Пусть событие А = {Петр будет готовить яичницу дважды}

I способ. Общее число способов выбрать три яйца из десяти равно

Петру придется переделывать завтрак, если ему попадется или одно или два испорченных яйца, т.е.

.

Тогда

.

II способ. Петру не придется заново готовить яичницу в том случае, если все три яйца окажутся свежими, т.е.

.

Тогда

.

Ответ: .

Задача 22. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий:

a) A={все пассажиры выйдут на четвёртом этаже};

b) B={Все пассажиры выйдут одновременно (на одном и том же этаже)};

c) C={все пассажиры выйдут на разных этажах}.

Решение. Общее число исходов

.

a) Появлению события 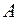благоприятствует единственный исход, т.е. . Тогда

.

b) Так как этажей на которых можно выйти шесть, то число исходов, благоприятствующих событию B . Тогда

.

c) Для события С число способов, которыми можно распределить трех человек по шести этажам равно . Таким образом

.

Ответ: a) ; b) ; c) .

Задача 23.Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.

Решение. Обозначим 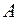= {появление бракованных книг}. Согласно формуле (4.1), относительная появления события 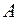равна

.

Ответ: 0,05.

Задача 24. Относительная частота попадания стрелком в цель равна 0,8.

Найти общее число выстрелов, если было зафиксировано 100 попаданий.

Решение. По формуле (4.1)

.

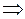
Ответ: 125 выстрелов.

Задача 25. При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных проборов, если всего было произведено 200 приборов.

Решение. По формуле (4.1)

.

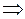
Ответ: 180 приборов.

Задача 26.В некотором городе в течение первого квартала родились: в январе – 145 мальчиков и 135 девочек, в феврале – 142 мальчика и 136 девочек, в марте – 152 мальчика и 140 девочек. Какова вероятность рождения мальчика? Найти отклонение вероятности от относительной частоты.

Решение. Вычислим частоту рождения мальчиков в каждом месяце:

;

;

За статистическую вероятность рождения мальчика в первом квартале можно принять среднее арифметическое относительной частоты за эти месяцы, т.е.

.

Отклонение от вероятности в январе равно 0,002; в феврале – 0,005; в марте – 0,004.

Ответ: 0,516.

Задача 27. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно (рис. 7.5). Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение. Искомая вероятность, согласно формуле (5.3), равна отношению площади кольца (фигура G) к площади большого круга 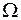. Найдем эти площади.

Площадь кольца Площадь большого круга

Тогда вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, равна

Ответ:

Задача 28. Корабль длиной 200 м и шириной 20 м имеет 4 круглые башни диаметром 4,5 м каждая. Найти вероятность поражения любой башни авиабомбой, если попадание бомбы в любую точку палубы равновозможно. Форма палубы принимается за эллипс, высота башни не учитывается.

Решение.

Найдем площадь палубы корабля (эллипса с полуосями 100 м. и 10 м.):

Появлению события А— поражения любой башни авиабомбой, благоприятствует множество точек, лежащих внутри каждой башни (круга диаметра 4,5 м). Площадь основания каждой башни равна:

Тогда вероятность события А равна

Ответ: 0,02025.

Задача 29. На прямолинейном участке газопровода длиной 130 км произошел разрыв. Какова вероятность того, что разрыв удален от обоих концов участка на расстоянии, большее 50 км?

Решение. Участок газопровода AB разобьем точками разрыва C и D (рис. 7.7). В нашем случае разрыв должен произойти на участке CD.

Рис. 7.7

Тогда вероятность искомого события равна

.

Ответ: .

Задача 30. Алексей и Иван на большой перемене договорились пойти пообедать в столовую. Большая перемена начинается в 13.00 и заканчивается в 13.30. Друзья условились ждать друг друга не более 15 мин. Какова вероятность того, что Алексей и Иван пообедают вместе?

Решение.

Пусть элементарное событие характеризуется двумя параметрами: – момент прихода в столовую Алексея, – момент прихода в столовую Ивана. Изобразим это событие точкой с координатами на плоскости в системе . За начала отсчета примем 13 часов, за единицу измерения 1 час. Постоим на плоскости пространство элементарных событий 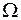. Это квадрат со стороной 0,5. Событие А – встреча, произойдет, если разность между и по абсолютной величине не превзойдет 0,25 часа (15 минут). Получаем неравенство .

1.

2.

Область благоприятных значений А (область G) заключена между прямыми и (рис. 7.8).

Рис. 7.8

Площадь области равна .

Площадь всего квадрата: .

Тогда искомая вероятность равна

.

Ответ: 0,75.

Задача 31. Стержень единичной длины произвольным образом разламывается на 3 част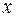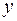и , и . Найти вероятность того, что из этих частей можно составить треугольник.

Решение.

Здесь два параметра, которые характеризует событие, это 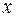и 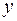, так как причем

Пространство элементарных событий 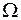– это область, ограниченная треугольником AOB (рис. 7.9). Его площадь .

Событие A = {из трех частей можно составить треугольник} выполняется, в том случае, когда:

1) сумма любых двух сторон больше третьей,

2) разность любых двух сторон меньше третьей.

То есть:

Итак, событие на плоскости представляет собой треугольник ECD (рис. 7.9), его площадь равна Тогда вероятность события А:

.

Ответ: .

Задача 32. На двух параллельных нефтепроводах, длина каждого из которых , а расстояние между ними , произошли порывы (по одному на каждом). Найти вероятность того, что расстояние между точками порывов будет не больше .

Решение. Абсциссу первой точки порыва обозначим 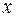, а второй 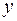; . Тогда искомое событие .

Рис. 7.10.